Особенности определения параметров сопротивления сдвигу скальных грунтов – экспериментальные и расчетные методы

ВВЕДЕНИЕ

При решении многих инженерно-геологических задач, в частности для расчетов устойчивости склонов, откосов, бортов карьеров, необходимы параметры прочности на сдвиг – сцепление (С) и угол внутреннего трения (φ) [6]. Традиционно они определяются по закону Кулона, который предполагает линейную зависимость между касательными и нормальными напряжениями:

τ=σ_n•tg φ+C,

где τ – касательное напряжение, σ_n – нормальное напряжение, φ – угол внутреннего трения, С – сцепление

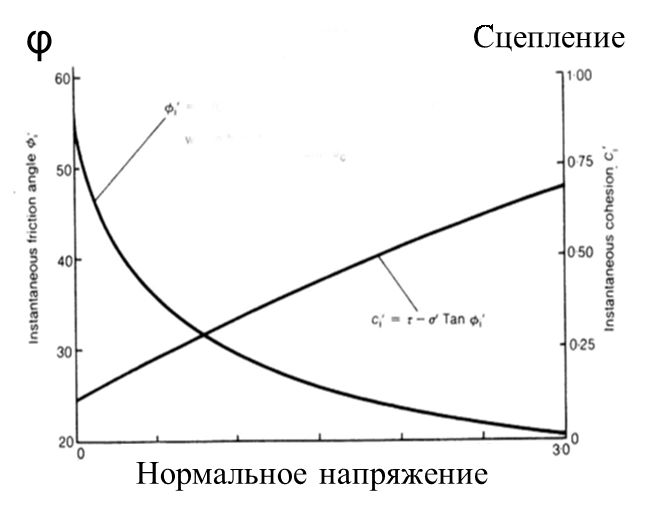
Однако линейная форма зависимости является лишь частным случаем, тогда как в общем случае данная зависимость имеет нелинейный характер. Соответственно, сдвиговые характеристики не являются константами, а зависят от величин напряжений, при которых они определяются: чем выше напряжения, тем больше сцепление и меньше угол внутреннего трения. Тенденция изменения параметров прочности на сдвиг в зависимости от нормальных напряжений наглядно показана на рис.1, заимствованном из работы Э. Хоека и Э.Т. Брауна (1980) [17].

Рис. 1. Тенденции изменения сцепления и угла внутреннего трения ц в зависимости от величины нормального напряжения [17]

Сложность определения сдвиговых характеристик скальных грунтов заключается не только в нелинейном характере предельной огибающей, но также и в том, что ее форма и степень нелинейности различны у разных типов грунтов. Другая проблема заключается в том, что массивы скальных грунтов находятся в напряженном состоянии вследствие воздействия гравитационных сил, которые на больших глубинах могут достигать значительных величин (например, при строительстве подземных сооружений – горных выработок, тоннелей, хранилищ и пр.), а также тектонических сил, характерных для горно-складчатых областей. Соответственно, это необходимо учитывать при определении прочности на сдвиг.

В зависимости от решаемой задачи определения параметров прочности на сдвиг могут быть проведены на образцах ненарушенной породы, по трещине или для скального массива.

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПРОЧНОСТИ НА СДВИГ НА ОБРАЗЦАХ СКАЛЬНЫХ ГРУНТОВ

Существует три основных способа определения сдвиговых характеристик образцов скальных грунтов [4, 10]: (1) построение паспорта прочности по данным прочности на одноосное сжатие (R_c) и растяжение (R_p); (2) срез со сжатием; (3) объемное сжатие.

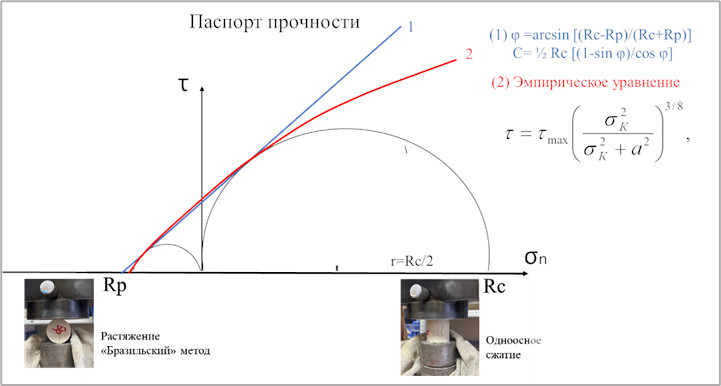
Построение предельной огибающей по данным определения прочности на одноосное сжатие (R_c) и растяжение (R_p) является наиболее простым и частно используемым методом. Он заключается в том, что в координатах касательные (τ) - нормальные (σ_n) напряжения строятся предельные круги Мора, соответствующие прочности на одноосное сжатие [2] и растяжение [3], и к ним проводится огибающая – либо линейная в виде касательной к кругам, либо нелинейная, с использованием эмпирического уравнения, указанного в [4] (рис.2). Преимуществом данного метода является то, что он не требует специального оборудования, кроме пресса. Однако его можно применять для определения сдвиговых характеристик лишь при небольших давлениях, тогда как в области высоких напряжений можно ожидать большой погрешности и расхождения результатов с реальными величинами.

Рис. 2. Паспорт прочности скального грунта, построенный по данным определения прочности на одноосное сжатие (Rc) и растяжение (Rp)

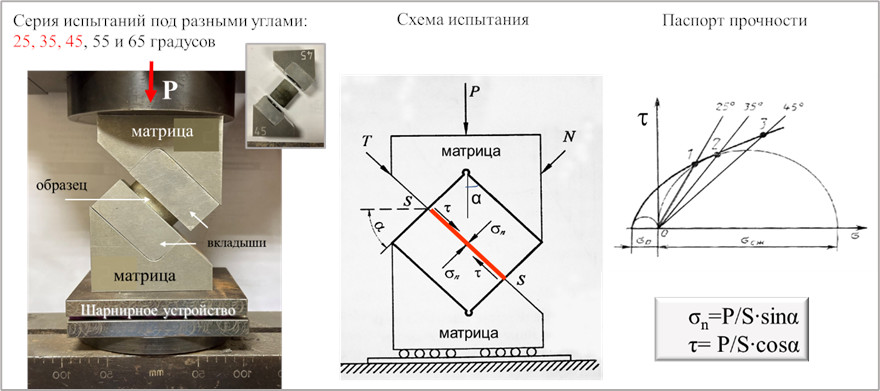
Срез со сжатием, являющийся еще одним способом получения предельной огибающей и определения сдвиговых характеристик, предполагает наличие специального устройства [5] (рис.3). Авторы проводили испытания при помощи устройства, разработанного и сконструированного И.Е. Большаковым согласно ГОСТ 21153.5-88 [5]. Метод заключается в разрушении образца по заданной плоскости среза при приложении к нему сжимающей вертикальной нагрузки. В комплект испытательного устройства входит от трех до пяти пар разъемных матриц (верхняя и нижняя) с вкладышами-обоймами для фиксирования образца. Зазор между верхней и нижней частями матриц расположен под разными углами по отношению к вертикали (обычно 25°, 35°, 45°, 55°, 65°). Нижняя матрица помещается на специальную подвижную платформу с шарнирным устройством. Собранное испытательное устройство с помещенным в него образцом скального грунта устанавливается в испытательную машину (пресс), где через стальные плиты к нему прикладывается сжимающая нагрузка. При достижении критической величины нагрузки происходит срез образца по заданной плоскости между обоймами. По результатам испытания рассчитывают нормальное σ_n и касательное τ напряжения, действующие в плоскости среза:

σ_n= cosα•P/S,

τ=sinα•P/S,

где Р – разрушающее усилие, S – площадь среза, α – угол наклона плоскости среза к направлению внешнего усилия

Рис.3. Построение предельной огибающей по результатам среза со сжатием

Проводят серию испытаний (минимум три) образца на срез под разными углами. По результатам опытов строят предельную огибающую τ=f(σ_n), по которой определяют сцепление и угол внутреннего трения. Паспорт прочности, полученный по результатам среза со сжатием, можно дополнить кругами Мора, построенными по данным R_c и R_p (см. рис.3) [4].

Объемное сжатие является наиболее точным, но и наиболее трудоемким методом определения С и φ. Он предполагает наличие специальной камеры для объемного сжатия [4, 10]. Его преимуществом является то, что он позволяет получить сдвиговые характеристики в условиях, максимально приближенных к естественным, в том числе и при высоких давлениях. Для получения предельной огибающей необходимо провести не менее трех испытаний в специальной камере для объемного сжатия при разных боковых давлениях по схеме σ1> σ2=σ3. По результатам нескольких испытаний в координатах τ-σ_n строится серия предельных кругов Мора, к которым проводится огибающая. Полученный по результатам объемного сжатия паспорт прочности можно дополнить кругами Мора, построенными по данным одноосного сжатия и растяжения.

Сравнение результатов определения сдвиговых характеристик разными методами на примере известняков

Для известняков Московского региона (С₂ mč) проведена серия испытаний по определению сдвиговых характеристик с использованием трех вышеописанных методов. Известняки без примесей, относительно однородные, мелкозернистые, тонкопористые, с плотностью 1,95-2,02 г/см³ и пористостью 25-30%. На рисунке 4 представлен пример наиболее типичных результатов, полученных тремя методами.

Рис. 4. Предельные огибающие, построенные по данным испытаний образцов известняка тремя разными методами

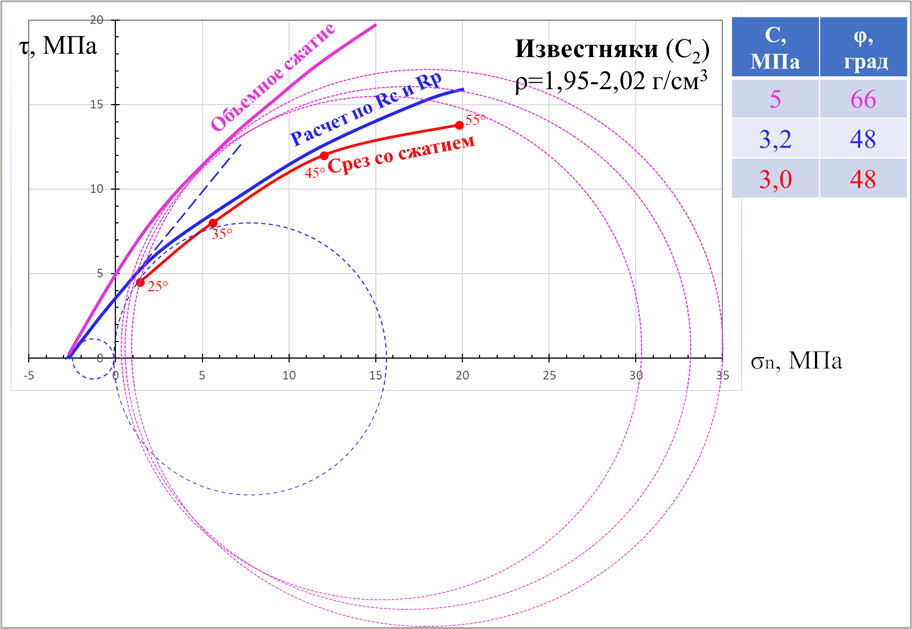
Предельные огибающие, построенные по результатам первых двух методов практически совпадают, тогда как огибающая, характеризующая объемное сжатие, проходит значительно выше и под большим углом. Чтобы объяснить выявленную закономерность необходимо провести дополнительные эксперименты, в том числе при объемном сжатии с более высокими величинами бокового давления.

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПРОЧНОСТИ НА СДВИГ ПО ТРЕЩИАМ В СКАЛЬНЫХ ГРУНТАХ

Все массивы горных пород содержат неоднородности в виде поверхностей напластования, ослабленных зон контактов, трещин различной природы, разрывных нарушений с зеркалами скольжения и иных, и в ряде случаев устойчивость склона определяется не прочностью самих пород, а прочностью по поверхностям ослабления [6, 9]. К неблагоприятным сценариям относятся случаи, когда слои или трещины падают в направлении склона и поверхность скольжения может частично или полностью совпадать с поверхностью ослабления. В этих случаях при расчетах устойчивости склонов необходимо знать параметры прочности на сдвиг по трещине.

Методы определения сдвиговых характеристик по трещине делятся на экспериментальные (полевые и лабораторные) и расчетные эмпирические.

Среди экспериментальных методов используются: (1) крупномасштабные полевые опыты in situ по срезу больших целиков с трещиной в основании (уникальные, трудоемкие, дорогие); (2) лабораторные испытания образца с трещиной (естественной или модельной) в приборе плоскостного среза [8, 9, 13]; (3) лабораторные трехосные испытания образца с трещиной [8].

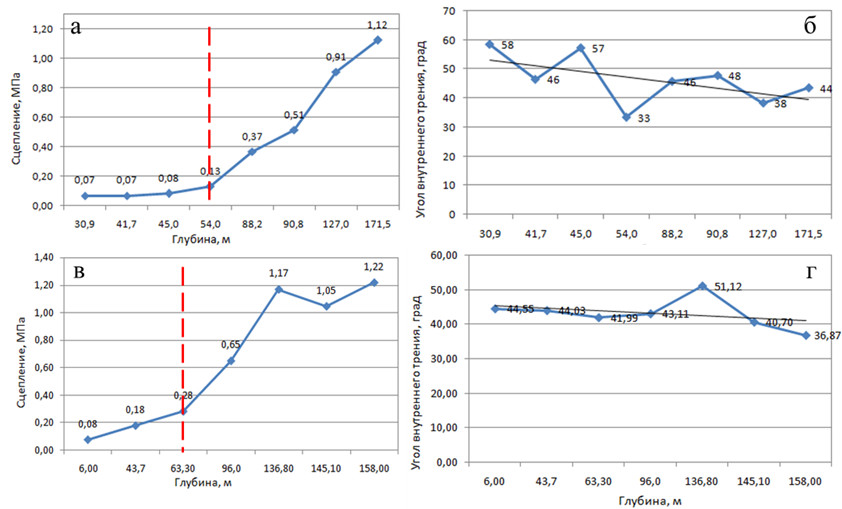
Среди расчетных методов применяются различные эмпирические уравнения, позволяющие оценить прочность трещины на сдвиг с учетом морфологических особенностей поверхности, геометрических размеров, наличия и типа заполнителя, прочности стенок и иных факторов [1, 9, 14, 20]. Одним из наиболее известных является уравнение Н. Бартона (1985) [14]:

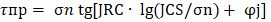
JRC – коэффициент шероховатости трещины (оценивается в баллах 0-20)

JCS – прочность на сжатие материала стенки трещины

σ_n – действующее нормальное напряжение

φ_j – угол трения по трещине (~ φ ост)

Слагаемое JRC lg(JCS/ σ_n) = i характеризует угол наклона макровыступа

В настоящее время для моделирования сдвига по трещине и определения параметров прочности используют ПО Particle Flow Code (PFC^2D), которое учитывает прочность материала стенок трещины, геометрические размеры, различные параметры неровности и шероховатости поверхностей, размер частиц / кристаллов породы и прочность связей между ними в процессе сдвига [22]. Морфологические особенности поверхности трещины, используемые в расчетах, отражены на ее цифровой модели, получаемой с помощью оптического сканирования.

Лабораторные испытания на срез по трещине проведены на образцах метавулканитов (К₂) Анадырского района в связи проектированием карьера и расчетами устойчивости бортов. Испытание производилось при помощи прибора одноплоскостного среза АСИС в соответствии с требованиями стандарта ASTM D5607 [13] (рис. 5).

Из керна производился отбор образцов с наиболее значимыми и потенциально опасными для устойчивости бортов карьера трещинами. Из каждого образца с трещиной при помощи камнерезного станка вырезалась призма, состоящая из двух частей, разделенных трещиной (плоскость трещины параллельна торцевым поверхностям призмы). Подготовленные образцы фиксировались в специальных кольцах (сконструированных И.Е. Большаковым, чтобы избежать использования цементирующих материалов) и помещались в сдвиговой прибор, где производилось испытание на срез по трещине при трех различных величинах нормальный нагрузки. В качестве первой ступени выбиралась бытовая нагрузка, определенная исходя из глубины залегания образца. Две последующие ступени принимались в соответствии с первой величиной нормального напряжения. Испытание завершалось при достижении относительной деформации равной 15-20%.

Рис. 5. Процедура проведения и обработки результатов испытания на срез по трещине

По итогам трех опытов при различных нормальных нагрузках строился график зависимости касательных напряжений от нормальных (рис. 8) в виде аппроксимирующей прямой, по которой вычислялись сцепление и угол внутреннего трения для исследованной трещины.

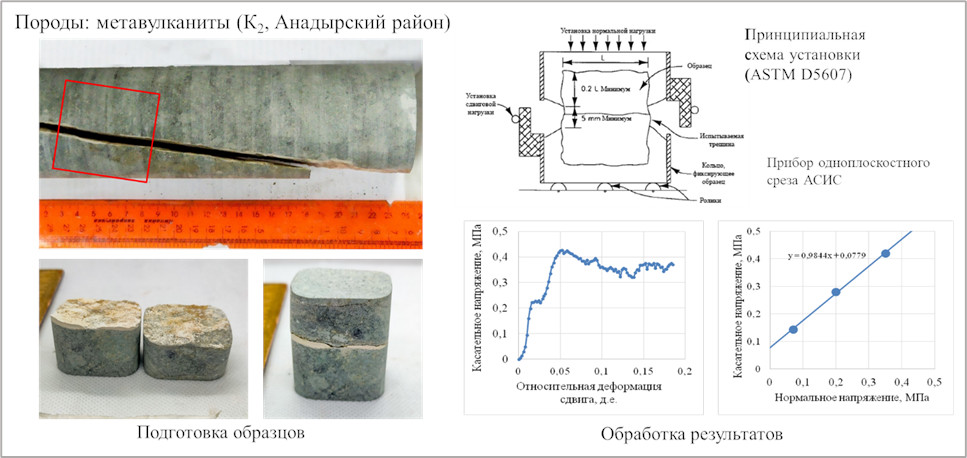
На рисунке 6 представлены диаграммы сдвига для исследованных трещин.

Рис. 6. Графики зависимости касательных напряжений от нормальных, полученные по данным испытаний на срез по трещине для метавулканитов

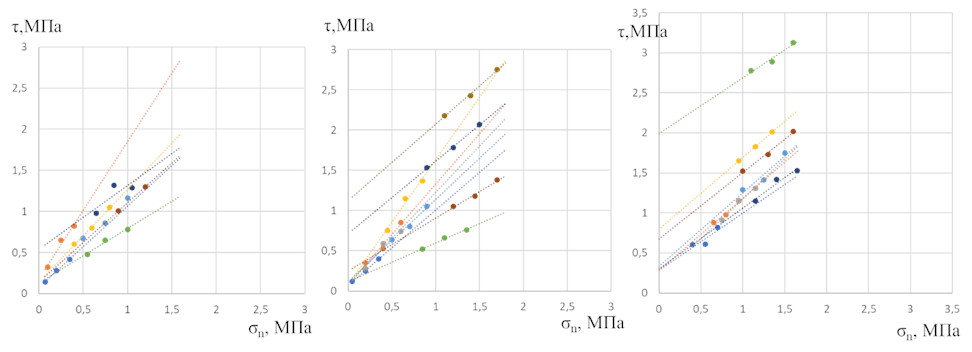
Выполненные испытания на срез по трещине показали изменчивость показателей С и φ в зависимости от величины нормальной нагрузки и, соответственно, от глубины отбора образца (рис. 7). Величина сцепления в целом повышается с увеличением глубины, однако на кривой (рис. 7 а, в) выделяются два участка, что в целом соответствует идеализированной модели сдвига по трещине с регулярной макрошероховатой поверхностью пилообразного типа (рис. 8) [9, 21]. Первый участок пологий, он отражает минимальные значения сцепления при низких величинах нормального напряжения (рис. 7 а, в). На этом этапе происходит сдвиг по поверхности имеющихся макровыступов и неровностей, за счет чего угол внутреннего трения увеличивается на величину, равную углу неровности (зубца) (рис. 8 б). При этом если микрошероховатость отсутствует, то есть поверхности гладкие, то сцепления между ними практически нет. При увеличении нормальной нагрузки начинается сдвиг с разрушением и срезом зубцов, при этом угол внутреннего трения снижается, но появляется сцепление за счет сопротивления зубцов (рис. 8 в). Угол внутреннего трения снижается с увеличением нормальной нагрузки (рис. 7 б, г).

Рис. 7. Зависимость сцепления и угла внутреннего трения по поверхности трещины от глубины отбора образца: а, б – первая система трещин; в, г – вторая система трещин

Рис. 8. Идеализированная модель среза по шероховатой трещине [8]: а – предельная огибающая, б – срез при низких величинах нормальной нагрузки по зубцам шероховатостей, в – срез при высоких величинах нормальной нагрузки с разрушением неровностей на поверхности трещины

Таким образом, при определении сдвиговых характеристик по трещине необходимо учитывать их зависимость от нормальной нагрузки и выбирать величины последней с учетом глубины интересующего интервала.

Сравнение сдвиговых характеристик, определенных для образцов и по трещинам показали, что в первом случае сцепление выше на 2-3 порядка значений (С_ср = 11 МПа у образца и С_ср = 0,07-0,28 МПа по трещинам). Угол внутреннего трения также выше у образцов, но разница не столь существенна (φ_cр= 53° у образцов, φ_cр= 42-50° по трещинам). Следует отметить, что параметры прочности на сдвиг по трещинам зависят от многих факторов, и в первую очередь от морфологии стенок, геометрических размеров, выветрелости, заполнителя, наличия воды. Влияние перечисленных факторов на сдвиговые характеристики требует отдельного анализа.

ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ПРОЧНОСТИ НА СДВИГ МАССИВА СКАЛЬНЫХ ГРУНТОВ

В инженерной геологии во многих случаях при решении практических задач требуется изучение и оценка горных пород в естественных условиях, для которых характерна изменчивость состава, строения и состояния, наличие различного рода неоднородностей (выветрелости, трещиноватости, сланцеватости и т.д.), а также анизотропия физико-механических свойств. При этом традиционный подход к изучению грунтов – разностороннее исследование отобранных образцов не обеспечивает полноты оценки состояния и характеристик скальных массивов [7, 11, 12]. Вместе с тем, оценка прочностных свойств скальных массивов является весьма сложной, неоднозначной и трудоемкой задачей. Традиционно применяются три группы методов: (1) полевые крупномасштабные испытания in situ; (2) косвенные методы, позволяющее осуществлять переход от свойств образца к свойствам массива на основе сочетания геологических, лабораторных инженерно-геологических и геофизических данных; (3) эмпирические геомеханические классификации и критерии прочности, основанные на учете свойств грунта и некоторых параметров массива, в наибольшей степени влияющих на его свойства (трещиноватость, обводненность, НДС и др.).

Расчет сдвиговых характеристик массива метавулканитов с использованием эмпирического критерия прочности Хоека-Брауна (Hoek-Brown failure criterion)

В настоящее время для оценки свойств скальных массивов широко используется эмпирический критерий прочности, предложенный Э. Хоеком и Э. Брауном [17, 18]. Он является развитием критерия прочности Кулона-Мора. Усовершенствование заключается в нелинейной форме предельной огибающей, которая в большей степени соответствует реальному деформированию скального грунта, особенно в области высоких напряжений. Предложенная методика оценки прочностных свойств скального массива основана на многолетнем анализе большого количества экспериментальных данных, полученных как при лабораторных испытаниях, так и при крупномасштабных полевых опытах. В модель Хоека-Брауна входят две группы параметров: 1) показатели, характеризующие прочностные свойства образца скального грунта – прочность на одноосное сжатие образца (σ_ci) и эмпирический коэффициент, отражающий степень взаимного зацепления минеральных частиц ненарушенного скального грунта и влияющий на степень нелинейности предельной огибающей Хоека-Брауна (m_i); 2) параметры, характеризующие нарушенность скального массива – геологический индекс прочности (GSI) и показатель техногенной нарушенности массива (D) [17, 18].

Обобщенный критерий Хоека-Брауна для трещиноватых массивов имеет вид:

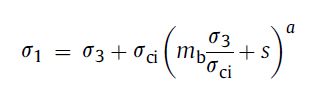
где σ1, σ3 – главные нормальные напряжения (максимальное и минимальное); m_b, s, а – безразмерные эмпирические коэффициенты, влияющие на форму и степень нелинейности предельной огибающей Хоека. Они зависят от геологического индекса прочности GSI и коэффициента техногенной нарушенности D.

Геологический индекс прочности GSI представляет собой эмпирический показатель, позволяющий количественно (в баллах от 0 до 100) оценить состояние скального массива в зависимости от его трещиноватости и степени сохранности. По сути, это двухпараметровая рейтинговая эмпирическая классификация, в которую в качестве параметров входят блочность (степень нарушенности массива) и характер поверхности трещин. Существуют различные методики определения величины GSI [19]. В данной работе расчет GSI производился по керну скважин через показатель трещиноватости J_Cond89 [15] и показатель качества керна RQD [16]:

Зная значения параметров GSI и D, рассчитывались эмпирические коэффициенты m_b, s, а, входящие в критерий Хоека-Брауна, а затем вычислялись показатели прочностных свойств скального массива, в том числе, сцепение C и угол внутреннего трения ц [18]:

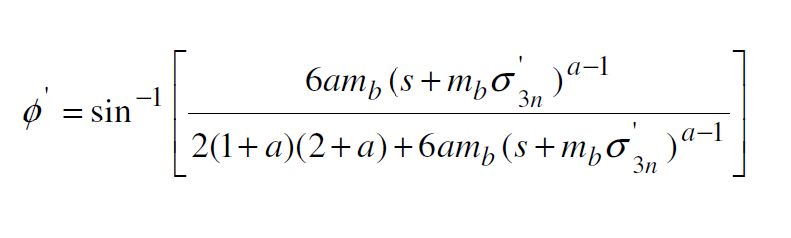
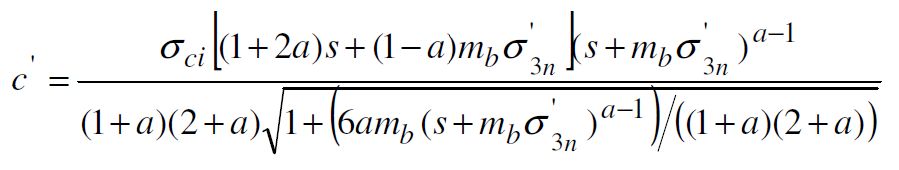
Вычисления производились с помощью программного обеспечения «RocLab» (Rocscience Inc).

На рисунке 9 представлена предельная огибающая, полученная для массива метавулканитов (входные параметры: R_c=64 МПа, m_i=22, GSI=61). В табл.1 приведены полученные значения С и φ при различных величинах нормального напряжения. Так, при увеличении величины σ_n  от 1 до 10 МПа, сцепление увеличивается в 4 раза, а угол внутреннего трения снижается от 61 до 44°.

Рис. 9. Предельная огибающая Хоека-Брауна, полученная для массива метавулканитов

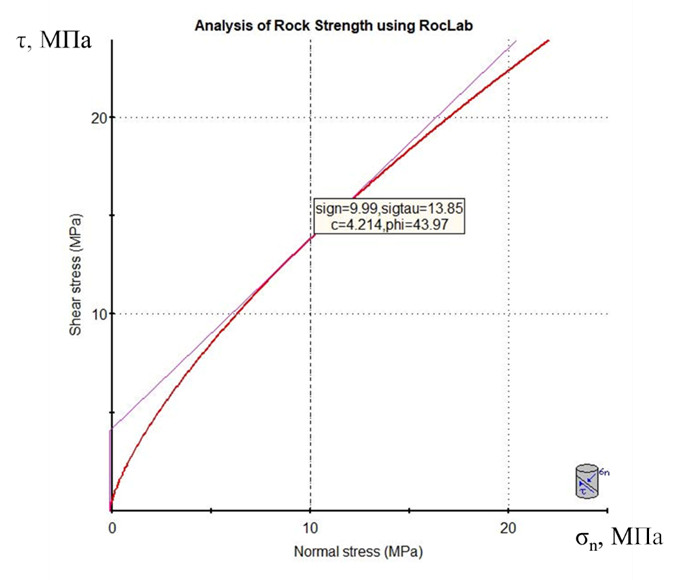
Таблица. Зависимость значений С и φ массива метавулканитов от величины нормального напряжения

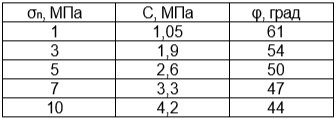
Вычисленные для массива величины сцепления примерно на порядок меньше, чем сцепление, характерное для образцов ненарушенной породы (С_ср = 11 МПа).

ЗАКЛЮЧЕНИЕ

Обобщение научно-практической и методической литературы по вопросу сопротивления скальных грунтов сдвигу, и проведенные эксперименты и расчеты для конкретных объектов, позволили сделать следующие выводы.

1. В зависимости от особенностей исследуемого массива и решаемой задачи инженер-геолог должен четко представлять, для какого объекта следует определять параметры прочности на сдвиг – для образца, поверхностей ослабления (трещин) или скального массива.

2. Важным вопросом является рациональный выбор и научное обоснование методики определения показателей сопротивления сдвигу. Это могут быть как прямые испытания (полевые или лабораторные), так и расчетные способы и эмпирические уравнения, у каждого метода есть свои преимущества и недостатки.

3. При выборе значений сдвиговых характеристик (С, φ), которые будут использоваться в расчетах, необходимо учитывать нелинейность предельной огибающей и, соответственно, их зависимость от интервала напряжений, для которого они определяются.

Список литературы

1. Газиев Э.М. Устойчивость скальных массивов и методы их закрепления. М.: Стройиздат. 1977.
2. ГОСТ 21153.2-84. Породы горные. Методы определения предела прочности при одноосном сжатии. М.: Изд-во стандартов, 2001 (с изм. №1 и №2).
3. ГОСТ 21153.3-85. Породы горные. Методы определения предела прочности при одноосном растяжении. М.: Изд-во стандартов, 1985.
4. ГОСТ 21153.8-88. Породы горные. Методы определения предела прочности при объемном сжатии. М.: Изд-во стандартов, 1989.
5. ГОСТ 21153.5-88. Породы горные. Метод определения предела прочности при срезе со сжатием. М.: Изд-во стандартов, 1988.
6. Зеркаль О.В., Фоменко И.К. Оползни в скальных грунтах и оценка их устойчивости // Инженерная геология, 2016. №4. С. 4-21.
7. Зеркаль О.В., Фоменко И.К., Фролова Ю.В. Классификация массивов скальных грунтов как инструмент изучения и оценки их поведения // Материалы годичной сессии Научного совета РАН по проблемам геоэкологии, инженерной геологии и гидрогеологии. Сергеевские чтения. «Массивы грунтов как жизнеобеспечивающий ресурс общества». М.: «ГеоИнфо», 2025. Вып.26. С. 94-98.
8. Зерцалов М.Г. Механика грунтов (введение в механику скальных массивов). М.: Ассоциация строительных вузов, 2006.
9. Могилевская С.Е. Экспресс-метод определения параметров сопротивления сдвигу скальных пород по трещинам. Основные положения. Экспериментальное и теоретическое обоснование. СПб., 2011. 236 с.
10. Фролова Ю.В. Скальные грунты и методы их лабораторного изучения. М.: КДУ, 2015. 222 с.
11. Фролова Ю.В., Зеркаль О.В. Современные методы определения прочностных свойств скальных и полускальных грунтов при оценке устойчивости склонов // Современные проблемы инженерной геодинамики: Тр. Юбилейной конференции, посвященной 100-летию со дня рождения проф. Г.С. Золотарева. М.: Изд-во Моск. ун-та, 2014. С. 146-150.
12. Фролова Ю.В., Зеркаль О.В. Современные методы определения прочностных свойств скальных и полускальных грунтов//Инженерная геология Северо-Западного Кавказа и Предкавказья: современное состояние и основные задачи / Матер. III региональной научно-практ. конф. (Краснодар, 24-25.11.2016). Краснодар: Изд-во Кубан. гос. ун-т, 2016, С. 273-277.
13. ASTM D5607-16 Standard Test Method for Performing Laboratory Direct Shear Strength Tests of Rock Specimens Under Constant Normal Force.
14. Barton N., Bandis S., Bakhtar K. Strength, deformation and conductivity coupling of rock joints. Int. J. Rock Mech. Min. Sci. and Geomech. Abstr. V.22. №3 1985. P. 121-140.
15. Bieniawski Z.T. Engineering rock mass classifications. New York, Wiley. 1989. 251 p.
16. Deere D.U. Technical description of rock cores for engineering purposes // Rock. Mech and Eng. Geol. 1963. 1(1). P. 16-22.
17. Hoek E., Brown E.T. Empirical strength criterion for rock masses. J. Geotech. Engin. Div., ASCE, 1980. Vol. 106, No. GT9, 1013-1035.
18. Hoek E., Brown E.T. The Hoek-Brown failure criterion and GSI - 2018 edition // J. of Rock Mechanics and Geotechnical Engineering. 2019. Vol. 11. P. 445-463.
19. Hoek E., Diederichs M.S. Quantification of the geological strength index chart // Proc. of the 2013 US Rock Mechanics / Geomechanics Symposium. San Francisco, 2013.
20. Ladanyi B., Archambault G. Simulation of shear behavior of a jointed rock mass. The 11th US Symp. on Rock Mechanics (USRMS). American Rock Mechanics Association. 1969.
21. Patton F. Multiple modes of shear failure in rocks. Proceeding 1st Congress Int. Soc. Rock Mech., Lisboa, 1966. V.1. P.509-513.
22. Rios-Bayona F., Johansson F., Mas-Ivars D., Sanchez-Juncal A., Bolin A. Using PFC2D to simulate the shear behavior of joints in hard crystalline rock // Bulletin of Engineering Geology. 2022. 81 (381). https://doi.org/10.1007/s10064-022-02885-8.