Расчет критической длины анкеров, противодействующих гидростатическому подъему. Часть 2

Расчет смещений стального анкера

Результаты большого количества испытаний показали, что под действием выдергивающей (вытягивающей) нагрузки напряжение сдвига между стальным стержнем анкера и материалом, скрепляющим его с грунтом, достигает своего максимального значения на очень небольшой глубине от устья скважины, затем постепенно уменьшается с глубиной и наконец на определенном вертикальном расстоянии от устья уменьшается до нуля [14].

Чтобы упростить расчет, распределение напряжений сдвига в стальном стержне анкера можно рассматривать как распределение по закону «перевернутого прямоугольного треугольника», в соответствии с которым оно достигает максимального значения на поверхности массива грунта (на уровне устья скважины), затем линейно уменьшается с глубиной и падает до нуля на глубине, равной критической длине анкера, как показано на рисунке 3.

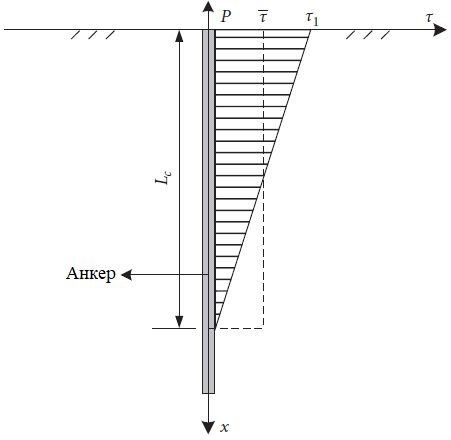
Рис. 3. Упрощенная модель распределения напряжений сдвига вдоль стального стержневого анкера. Буквенные обозначения: P – вытягивающая нагрузка, действующая на анкер; L_c – критическая длина анкера; τ₁ – напряжение сдвига на поверхности (на уровне устья скважины), а именно максимальное напряжение сдвига; ₸– среднее напряжение сдвига

В целях улучшения общей эффективности взаимодействия между стержнем анкера и материалом, скрепляющим его с грунтом (в упрощенной модели – с грунтом), Вон и др. [15] предложили метод определения среднего напряжения сдвига стержня (соответствующий режим распределения напряжений сдвига показан на рисунке 3 пунктирной линией) по следующей формуле:

Используется следующее соотношение между напряжением сдвига на поверхности и средним напряжением сдвига в рамках модели «перевернутого прямоугольного треугольника»:

Таким образом, функция распределения напряжений сдвига анкера в модели «перевернутого прямоугольного треугольника» выглядит так:

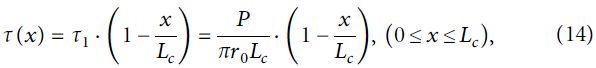
где τ(x) – напряжение сдвига на поверхности контакта между стержнем анкера и материалом, скрепляющим его с грунтом, на глубине, равной x.

Стержень анкера рассматривается как упругое тело, а функция распределения осевых усилий вдоль него представляется следующим образом:

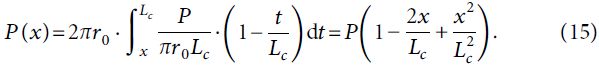
Согласно закону Гука упругое смещение верха стального стержня анкера может быть выражено так:

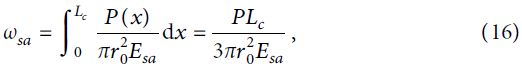
где E_sa – модуль упругости стального стержня анкера.

Расчет смещений стеклопластикового анкера

Модуль упругости стеклопластикового стержня анкера намного ниже, чем у стального, и поведение напряжений сдвига при выдергивающей (вытягивающей) нагрузке для них неодинаково. Результаты соответствующих испытаний [16–19] показывают, что по сравнению со стальным стержнем максимальное напряжение сдвига стеклопластикового стержня проявляется на большей глубине, чем для стального. При этом закон распределения напряжений сдвига по глубине для стеклопластикового анкера сильно отличается от модели «перевернутого прямоугольного треугольника». Поэтому необходимо усовершенствовать метод расчета смещений анкера, чтобы сделать его более подходящим для случая стеклопластикового стержня.

Как показано на рисунке 4, максимальное напряжение сдвига стеклопластикового стержня наблюдается на глубине L_x и по-прежнему составляет τ₁. Оно постепенно уменьшается от точки пика вверх вплоть до нуля на уровне устья скважины. Вниз от точки пика оно также постепенно уменьшается вплоть до нуля на глубине, соответствующей критической длине анкера L_c.

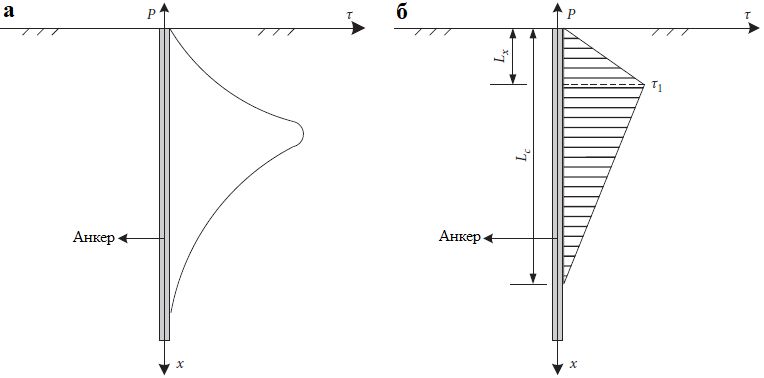
Рис. 4. Модель распределения напряжений сдвига по глубине для стеклопластикового анкера: а – теоретическая; б – упрощенная

Чтобы обеспечить неизменное общее напряжение сдвига, принимается, что τ₁ в модели для стеклопластикового анкера по-прежнему удовлетворяет зависимостям (12) и (13).

В соответствии с показанным на рисунке 4 распределение напряжений сдвига по глубине для стеклопластикового стержня выражается следующим образом:

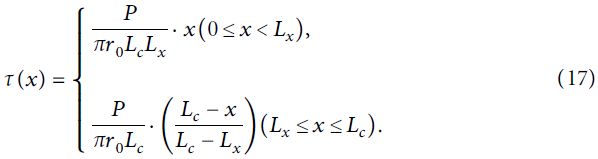
Распределение осевых усилий вдоль стержня выражается так:

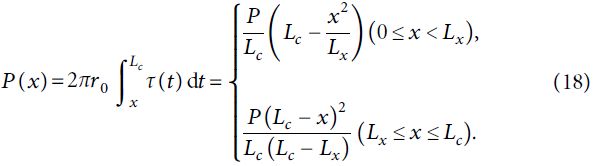
Согласно закону Гука упругое смещение верха стеклопластикового стержня анкера составляет:

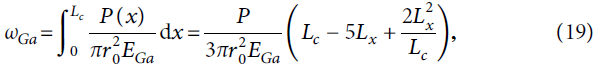
где E_Ga – модуль упругости стеклопластикового стержня анкера.

Расчет критической длины анкера

Если принять, что анкер деформируется в гармонии с окружающим грунтом, то смещение его верха должно быть равно смещению окружающего грунта. Задачи по нахождению критической длины анкеров со стальным и стеклопластиковым стержнем решаются отдельно.

1. Для стального анкера, подставив выражения (11) и (16) в уравнение (19) при ω_s=ω_sa, можно получить следующее уравнение:

Тогда модуль сдвига упругого грунта с модулем упругости E_s:

Подставив выражения (12), (13) и (21) в уравнение (20) и упростив результат, получим:

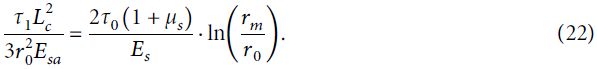
Напомним, что τ₀ в правой части уравнения (22) – это напряжение сдвига для самого внутреннего из концентрических цилиндров (то есть напряжение сдвига на границе раздела между анкером и окружающим грунтом, см. рис. 1), τ₁ в левой части уравнения (22) – это напряжение сдвига анкера на уровне устья скважины, то есть максимальное напряжение сдвига для стального стержня (см. рис. 3).

Уравнение (22) можно упростить, получив следующее:

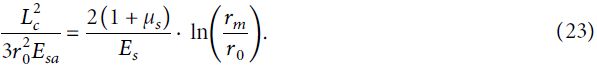
После упрощения уравнения (23) с учетом равенства (10) получится такая формула для нахождения критической длины стального стержня анкера:

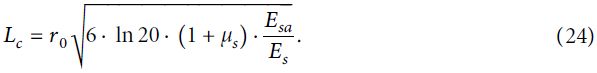
2. Для стеклопластикового анкера ω_s=ω_Ga. Подставив выражения (11) и (19) в это равенство, можно получить следующее уравнение:

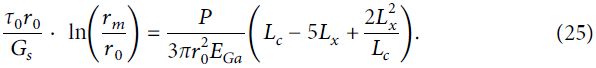
Используя тот же метод упрощения, что и для стального анкера, и подставив выражения (12), (13) и (21) в уравнение (24), можно получить такое уравнение:

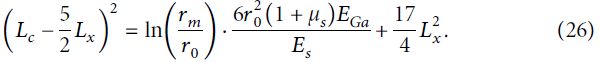
Тогда критическую длину стеклопластикового анкера можно найти по формуле:

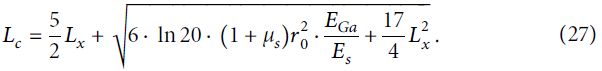
Кроме того, поскольку упрощенная модель распределения напряжений сдвига вдоль анкера не может сама по себе помочь определить глубину L_x, на которой напряжение сдвига стеклопластикового стержня максимально, авторы представленной в этой статье работы для решения этой проблемы использовали следующий метод.

Автор статьи [20] (с короткой фамилией Ю), чтобы найти распределение напряжений сдвига вдоль анкера, использовал решение задачи Миндлина:

где τ(x), как уже указывалось ранее, – это напряжение сдвига на поверхности контакта между стеклопластиковым стержнем и окружающим материалом (в упрощенной модели – с грунтом) на глубине x; а под буквенным обозначением t подразумевается следующее выражение:

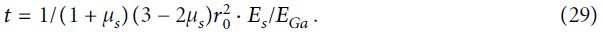
где µ_s – коэффициент Пуассона для грунта.

Поскольку распределение напряжений вдоль стеклопластикового анкера имеет только один пик, то точка, в которой производная выражения (28) равна нулю, может быть использована для определения глубины L_x. В соответствии с этим окончательный результат для x=L_x (то есть для точки с максимальным напряжением сдвига стеклопластикового анкера) будет следующим:

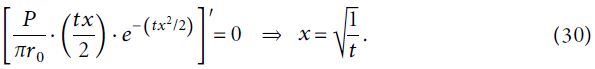
Тогда при подстановке уравнений (30) в формулу (27) получится следующее выражение для критической длины стеклопластикового стержня анкера:

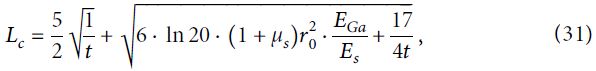
где t находится по формуле (29).

-

Продолжение перевода статьи (Nan Yan et al., 2021) появится в «Геоинфо» в ближайшие дни.

Источник для перевода

Nan Yan, Xueying Liu, Mingyi Zhang, Xiaoyu Bai, Zheng Kuang, Yongfeng Huang, Desheng Jing, Jun Yan, Cuicui Li, Zhongsheng Wang. Analytical calculation of critical anchoring length of steel bar and GFRP antifloating anchors in rock foundation // Hindawi. Mathematical Problems in Engineering. 2021. Vol. 2021. Article ID 7838042. 10 p. URL: doi.org/10.1155/2021/7838042; hindawi.com/journals/mpe/2021/7838042/.

Список литературы, использованной авторами переведенной работы (Nan Yan et al., 2021), можно посмотреть по адресу: hindawi.com/journals/mpe/2021/7838042/.