Расчет критической длины анкеров, противодействующих гидростатическому подъему. Часть 1

ВВЕДЕНИЕ

Анкеры, противодействующие гидростатическому всплытию, или подъему, плитных фундаментов (далее – анкеры) широко используются, так как они вызывают лишь небольшие концентрации напряжений, имеют простую технологию строительства и низкую стоимость [1–3]. Традиционные анкеры со стальными стержнями доказали свою эффективность в различных условиях, но они имеют короткий расчетный срок службы в суровых условиях с вызывающими коррозию подземными водами или электрическими токами, создаваемыми железнодорожной инфраструктурой. Это ограничение могут преодолеть неметаллические анкеры, среди которых стали особо выделяться анкеры из армированных стекловолокном полимеров (GFRP, композитные стекловолоконные анкеры) благодаря таким преимуществам, как высокая прочность на растяжение, устойчивость к коррозии и электромагнитным помехам, а также низкая стоимость [4–7].

В последние годы многие ученые в Китае и других странах проводили исследования эффективности анкеров.

Так, Чжан и др. [8] предложили нестационарную модель (с изменениями во времени) для описания зависимостей «нагрузка – деформация» для грунтовых нагелей из стеклопластика в процессе вытягивания (выдергивания) из грунта путем наблюдения за непрерывным взаимодействием между стеклопластиковыми нагелями и песком. Также ими были проведены реальные испытания для проверки достоверности предложенной аналитической модели.

Трехо и др. [9] исследовали поведение стеклопластиковых стержней, заделанных в бетон, в течение 7 лет. Чтобы лучше оценить потери несущей способности и соответствующие коэффициенты, необходима вероятностная модель изменений несущей способности встроенных в бетон стеклопластиковых стержней во времени. Чтобы улучшить работу анкера, длину его стержня обычно увеличивают.

Однако Бай и др. [10] в ходе полевых испытаний на выдергивание (вытягивание) анкеров обнаружили, что существует критическая длина их стальных и стеклопластиковых стержней, то есть анкер на определенной глубине уже не будет испытывать напряжений. Это указывает на то, что неограниченное увеличение его длины не может постоянно улучшать характеристики его работы против гидростатического всплытия и только приведет к выбросу на ветер материалов и увеличению стоимости. Поэтому для повышения эффективности строительства и экономии затрат очень важно найти точный метод расчета критической длины анкеров со стальными и стеклопластиковыми стержнями.

К настоящему времени имеется мало сообщений о методах расчета критической длины стальных и стеклопластиковых анкеров в скальных основаниях.

В исследовании, представленном в настоящей статье, был разработан метод расчета критической длины стальных и стеклопластиковых анкеров при объединении сдвиговой модели деформирования идеальных концентрических (коаксиальных) тонкостенных цилиндров и упрощенной модели распределения напряжений сдвига.

Была проверена достоверность предложенного метода путем сопоставления с результатами реальных измерений при испытаниях в полевых условиях и рассмотрено влияние соотношения модулей упругости анкера и скальной породы (E_a/E_s) на величину критической длины его стержня.

ТЕОРЕТИЧЕСКИЕ ОСНОВЫ

Расчеты геотехнических смещений

Учитывая, что механизм работы анкера против гидростатического подъема схож с таковым для анкерной сваи, для анализа работы такого анкера используются соответствующие теоретические основы для анкерный сваи. Если принять, что грунтовый массив, который вмещает анкер, является идеально упругим телом, а вещество, скрепляющее стержень анкера со стенками скважины, обладает теми же свойствами, что и окружающий грунт (скальный или дисперсный), без учета увеличения вертикального напряжения, то деформирование грунта под действием вытягивающей нагрузки может быть представлено с помощью сдвиговой модели идеальных концентрических (коаксиальных) тонкостенных цилиндров (рис. 1) [11, 12].

Анкер взаимодействует с окружающим грунтом, передавая вытягивающую нагрузку на прилегающие к нему и друг другу концентрические цилиндры (через n цилиндров). Используя метод выбора элементарных ячеек для решения трехмерных осесимметричных задач в рамках теории упругости, выбирают два цилиндра, разделенных расстоянием dr, две вертикальные плоскости на расстоянии dθ друг от друга и две горизонтальные плоскости, ограниченные тончайшим шестигранником, на расстоянии друг от друга, равном dz.

Поскольку модель концентрических (коаксиальных) цилиндров относится к осесимметричным задачам, в элементе тела из двух соседних цилиндров действуют только нормальные напряжения и вертикальные (осевые) напряжения сдвига. Для двух соседних плоскостей имеются только нормальные и радиальные напряжения сдвига. Для двух соседних вертикальных плоскостей существует только кольцевое напряжение, а приращение равно нулю. Силы, действующие на элементарную ячейку (см. рис. 1), отражены на рисунке 2.

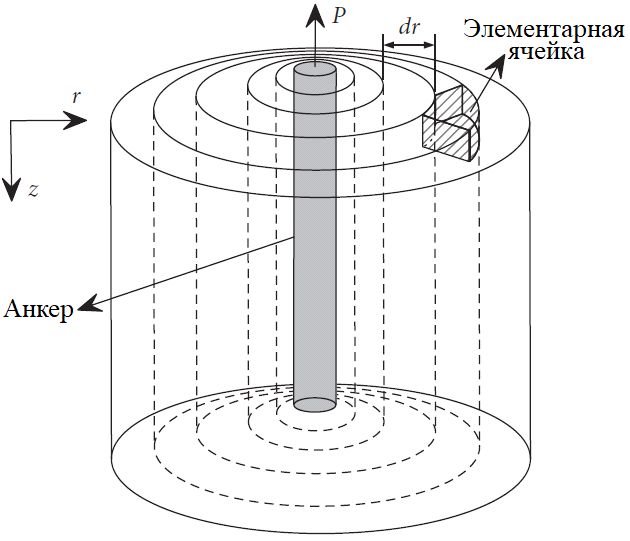
Рис. 1. Модель концентрических (коаксиальных) тонкостенных цилиндров. Буквенные обозначения: r – горизонтальное (радиальное) направление и расстояние между элементарной ячейкой и вертикальной осью цилиндров; dr – расстояние между соседними элементарными ячейками; P – вытягивающая нагрузка на анкер

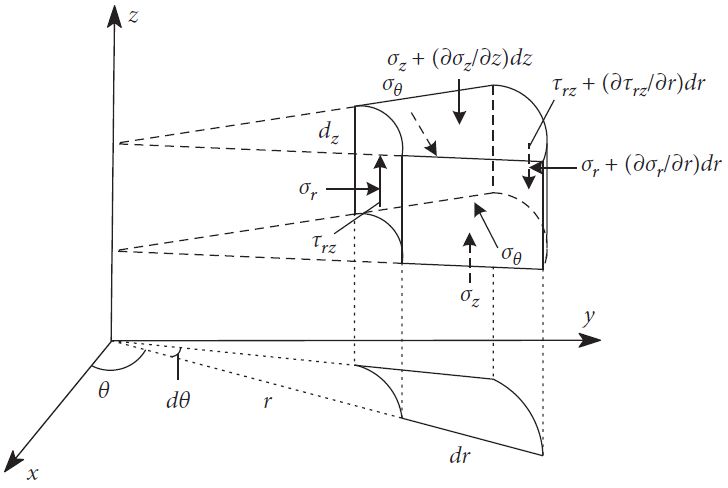
Рис. 2. Схематическое представление единичных сил. Буквенные обозначения: P – вытягивающая нагрузка на анкер; r – расстояние между элементарной ячейкой и вертикальной осью цилиндров Z; τ_rz – напряжение сдвига, действующее на цилиндр вдоль оси Z; θ – угол поворота элементарной ячейки относительно оси Х; σ_r, σ_θ и σ_z – нормальные напряжения в направлениях r, θ и Z соответственно

Как показано на рисунке 1, равновесие крутящих моментов модели относительно оси Z может быть получено при равенстве с усилием, приложенным к элементарной ячейке (см. рис. 2):

где τ₀ – напряжение сдвига на границе раздела между анкером и окружающим грунтом, r₀ – радиус анкера; r – расстояние между элементарной ячейкой и вертикальной осью цилиндров Z; τ_rz – напряжение сдвига, действующее на цилиндр вдоль оси Z.

Исходя из рисунка 2 и игнорируя физическое усилие для элементарной ячейки, можно получить следующее уравнение равновесия пространственной осесимметричной задачи теории упругости:

Когда на анкер действует растягивающая сила, изменение напряжения сдвига элементарной ячейки в грунте намного больше, чем для вертикального нормального напряжения. Поэтому можно принять, что:

то есть этим отношением можно пренебречь. Тогда уравнение (2) примет вид:

Интегрирование обеих частей уравнения (4) и объединение с уравнением (1) даст следующую формулу:

Приняв, что смещение элементарной ячейки на рисунке 2 в направлении оси Z равно ω, смещение в направлении r равно μ, а круговое смещение (в направлении θ) равно нулю, сдвиговое смещение можно выразить так:

где γ_rz – смещение сдвига элементарной ячейки; G_s – модуль сдвига вмещающего грунта.

Элементарная ячейка в основном имеет вертикальное смещение. Следовательно, при пренебрежении ее смещением вдоль направления r, уравнение (6) получит вид:

Для однородного грунта при использовании уравнений (5) и (7) можно получить:

Интегрирование уравнения (8) даст следующую формулу:

где ω_s – суммарное смещение грунта; r_m – эффективный радиус влияния вытягивающей нагрузки, за пределами которого этим влиянием на грунт можно пренебречь.

Кук и др. [13] установили, что грунт практически не деформируется на радиальном расстоянии, превышающем радиус анкера r₀ более чем в 20 раз, поэтому:

Используя уравнение (9), общее смещение грунта можно выразить так:

-

Продолжение перевода статьи (Nan Yan et al., 2021) появится в «Геоинфо» в ближайшие дни.

Источник для перевода

Nan Yan, Xueying Liu, Mingyi Zhang, Xiaoyu Bai, Zheng Kuang, Yongfeng Huang, Desheng Jing, Jun Yan, Cuicui Li, Zhongsheng Wang. Analytical calculation of critical anchoring length of steel bar and GFRP antifloating anchors in rock foundation // Hindawi. Mathematical Problems in Engineering. 2021. Vol. 2021. Article ID 7838042. 10 p. URL: doi.org/10.1155/2021/7838042; hindawi.com/journals/mpe/2021/7838042/.

Список литературы, использованной авторами переведенной работы (Nan Yan et al., 2021), можно посмотреть по адресу: doi.org/10.1155/2021/7838042; hindawi.com/journals/mpe/2021/7838042/.