Аналитический метод расчета осадки с учетом нелинейности деформирования

Введение

Несмотря на широкое распространение численных методов в практике геотехнического проектирования, аналитические решения задач по-прежнему актуальны – именно эти методы расчета осадки и устойчивости основания сооружения хорошо апробированы и являются достаточным обоснованием безопасности и надежности. В частности, метод послойного суммирования (МПС) на протяжении 50 лет является основным рекомендованным методом расчета осадки отдельно стоящих и ленточных фундаментов.

Ограничения аналитических методов хорошо известны: в большинстве случаев расчет не учитывает негоризонтального залегания ИГЭ, а поведение отдельных элементов моделируется на основании теории линейного деформирования. Метод послойного суммирования предполагает, что каждый элементарный слой находится в состоянии компрессионного сжатия, и не испытывает бокового расширения. Это предположение справедливо лишь отчасти, для фундаментов достаточно большой ширины по отношению к сжимаемой толще основания. Анализ напряженного состояния основания даже на основании теории линейно-деформируемой среды показывает, что области роста касательных напряжений хоть и не распространяется на ту же глубину, что нормальные напряжения, но не могут игнорироваться при расчете деформаций.

Профессором З.Г. Тер-Мартиросяном была предложена модификация этого метода, позволяющая учитывать развитие в каждом элементарном слое сдвиговых деформаций. Преимуществом данного метода является возможность учета деформации основания за счет формоизменения – даже при ν = 0,5, то есть при бесконечной объемной жесткости, осадка не будет нулевой за счет деформации сдвига. Помимо этого, использование параметров объемной и сдвиговой жесткости лучше соответствует физическим процессам, протекающим при деформировании скелета грунта (изменению пористости и взаимному смещению частиц). Однако сохраняется и общий недостаток теории линейного деформирования: в пределах одного ИГЭ жесткость не зависит от уровня действующих напряжений, и величина осадки напрямую зависит от выбора мощности сжимаемой толщи.

В качестве логичного дальнейшего шага можно воспользоваться хорошо известной в рамках нелинейной механики грунтов степенной зависимостью жесткости от уровня средних напряжений. Предлагаемая модификация позволит расширить область применения метода послойного суммирования, а также снизит зависимость результата расчета от выбора мощности сжимаемой толщи, так как с увеличением напряжений с глубиной жесткость будет возрастать, и затухание осадки будет происходить быстрее.

В настоящей работе приведены результаты сопоставления решений тестовой задачи различными методами.

Материалы и методы

По предложению З.Г. Тер-Мартиросяна осадка определялась по двучленной формуле, в которой для каждого элементарного слоя раздельно определялась деформация за счет объемного сжатия, вызванная изменением среднего напряжения, и деформация сдвига, вызванная девиатором напряжений:

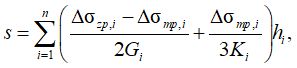
где s – осадка элементарного слоя; Δσ_zp,i – приращение дополнительного напряжения в середине i-го слоя; Δσ_mp,i – приращение дополнительного среднего напряжения в середине i-го слоя; G_i – модуль сдвига i-го слоя; K_i – модуль объемного сжатия i-го слоя; h_i – мощность i-го слоя.

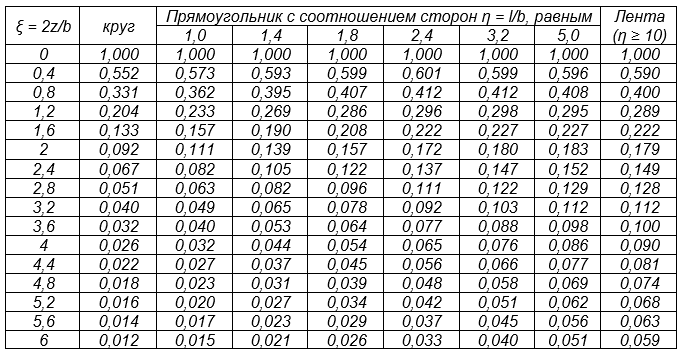
Некоторые вопросы в этой методике вызывает определение среднего напряжения для i-го слоя. В исходной редакции его предлагается рассчитывать на основании компонент напряженного состояния для данной точки [1]. Это может быть выполнено на основании решения задачи А. Лява [2], развитого впоследствии В.Г. Короткиным [3] – в его публикации приведены полные аналитические решения для всех компонентов НДС. Несмотря на громоздкость этих решений, величина приращений дополнительных напряжений определяется исключительно интенсивностью распределенной нагрузки, формой загруженной площади и координатами рассматриваемой точки, что позволяет выразить средние напряжения с помощью коэффициентов влияния. Принимая во внимание, что метод послойного суммирования исходно рассматривает только центральную ось, проходящую через загруженную площадь, можно также не рассматривать точки вне этой оси (x, y = 0). Таким образом, для определения Δσ_zp,i можно использовать табличные значения коэффициента влияния α (табл. 5.8. СП 22.13330.2016), а для определения Δσ_mp,i – получить свои значения коэффициентов, представленные в таблице 1. При необходимости, значения коэффициентов могут быть рассчитаны и для больших глубин.

Таблица 1. Коэффициенты влияния α_m для расчета средних напряжений Δσ_mp,i по оси загруженной площади (при ν = 0,3)

Характерно, что по мере увеличения соотношения сторон прямоугольной загруженной площади среднее напряжение с глубиной затухает медленнее (рис. 1). Для близкой к квадрату загруженной площади, напротив, наблюдается концентрация среднего напряжения в пределах глубины, равной ширине фундамента. Этот вывод вполне логичен, так как хорошо известно, что приращения горизонтальных напряжений с глубиной затухают крайне быстро, а степень затухания вертикальных напряжений непосредственно зависит от конфигурации загруженной площади. На этом основании можно предположить, что наибольшее расхождение между предлагаемым методом и классическим МПС будет наблюдаться для ленточных фундаментов, так как предлагаемое решение основано на пространственной, а не плоской задаче.

Рис. 1. Затухание вертикальных, средних и девиаторных напряжений с глубиной для загруженной площади с различным соотношением сторон

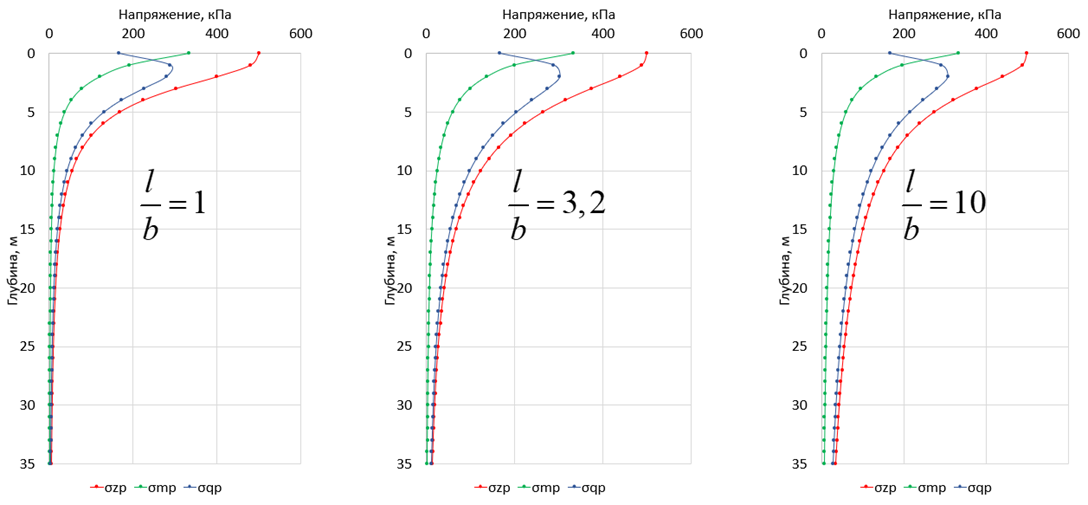
Следует отметить, что, в отличие от вертикального напряжения, горизонтальные напряжения (а, как следствие, и средние) зависят от величины коэффициента относительного поперечного расширения ν. В.А. Флорин указывает [4], что влияние коэффициента поперечного расширения несущественно влияет на значения напряжений, однако это верно только для квадратной загруженной площади. По мере увеличения соотношения l/b влияние увеличивается, и для ленточного фундамента (l/b > 10) расхождение между средними напряжениями при ν = 0,2 и ν = 0,4 достигает 21%.

Нелинейность деформирования в предлагаемом методе проще всего учесть путем введения степенной зависимости модулей жесткости от уровня средних напряжений. При этом авторам представляется более корректным использовать независимые показатели степени для сдвига и объемного сжатия – аналогично тому, как это сделано в модели UBCSand и ее модификациях [5–8]:

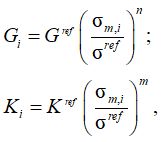
где G^ref, K^ref – опорные значения модулей сдвига и объемного сжатия, соответственно; σ^ref – опорное среднее давление; n, m – степенные показатели.

В отличие от широко распространенной в настоящее время модели Hardening Soil [9, 10], независимые показатели жесткости позволяют учитывать различие физических процессов, влияющих на изменение жесткости грунта при уплотнении. Сдвиговая жесткость обусловлена в первую очередь трением, и в грунтах с бомльшими значениями угла внутреннего трения зависимость будет более сильной. Объемная жесткость определяется пористостью, и для грунтов с плотной упаковкой частиц зависимость будет слабой. Данные степенные показатели могут быть определены по результатам испытаний трехосного и компрессионного сжатия в результате расчета, соответственно, значений параметров сдвиговой и объемной жесткости при различных уровнях средних напряжений и последующей аппроксимации полученных частных значений степенной функцией.

Начальное (бытовое) среднее напряжение σ_m,i в каждом элементарном слое, необходимое для учета нелинейной жесткости, целесообразно определять на основании бытового вертикального напряжения и величины коэффициента бокового давления в массиве K₀. В этом случае в расчете может быть учтено и переуплотненное состояние.

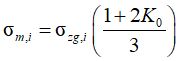
Порядок расчета практически не отличается от изложенного в СП 22.13330.2016. После построения эпюр природного и дополнительного давления и определения мощности сжимаемой толщи, вся она разделяется на элементарные слои. В уровне середины каждого слоя рассчитывается величина среднего бытового напряжения уm,i, на основании которого определяется величина модулей сдвига и объемного сжатия. Расчет может быть легко выполнен в табличной форме.

С целью сопоставления различных методов было выполнено три группы расчетов:

Для проверки точности аналитического решения был выполнен строгий расчет для невесомого основания для линейно-упругой среды методом послойного суммирования, методом З.Г. Тер-Мартиросяна и по решению Шлейхера-Польшина [11, 12]. Авторами была рассмотрена задача об осадке в центре загруженной площади шириной 1 м, нагрузка составила 500 кПа. Рассмотрено три случая соотношения сторон – загруженный квадрат, прямоугольник с соотношением сторон l/b = 3,2 и условно бесконечная лента. Нагрузка принята бесконечно гибкой для лучшего соответствия условиям метода послойного суммирования и аналитического решения задачи. Для наглядности рассматривался только случай первичного нагружения, без разгрузки, а сама нагрузка приложена к дневной поверхности массива. Мощность элементарного слоя принята равно 0,2 м.

Мощность сжимаемой толщи в данном случае искусственно не ограничивалась и составила 7 м (дополнительные напряжения от внешней нагрузки на этой глубине не превышают 1,5%).

Инженерный расчет в линейной постановке, учитывающий вес основания и более реалистичные геометрические параметры, выполнялся методом послойного суммирования по СП 22.13330.2016, предлагаемым аналитическим методом и численно в программном комплексе Plaxis. Использовалась линейно-упругая модель, расчет выполнялся методом послойного суммирования, методом З.Г. Тер-Мартиросяна в линейной постановке и численно. Ширина фундамента была принята равной 5 м, глубина заложения также 5 м. Как и для аналитического расчета, рассматривались соотношения сторон l/b = 1, 3,2 и 10. Мощность сжимаемой толщи определялась по методике СП 22.13330.2016 и использовалась для установления нижней границы расчетной модели. Для квадратной загруженной площади она составила 6 м; для прямоугольной – 9 м; для ленты – 10 м. Мощность элементарных слоев принималось равной 0,2b = 1м.

Для проверки учета нелинейности деформирования был выполнен расчет той же задачи предлагаемым нелинейным методом и с применением модели Hardening Soil, использующей аналогичный степенной закон изменения жесткости. Геометрические параметры задачи были приняты аналогично предыдущему варианту расчета.

Для корректного сопоставления результатов расчетов были приняты следующие параметры физико-механических свойств:

Таблица 2. Принятые в расчете параметры физико-механических свойств

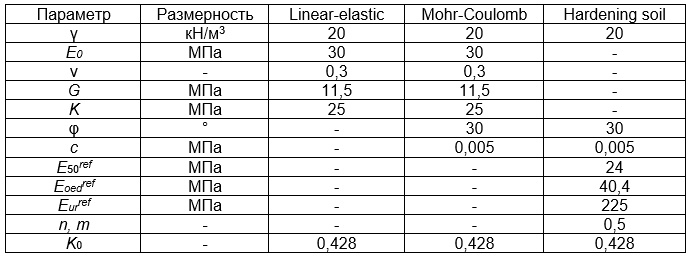
Результаты исследования

Результаты расчета осадки загруженной площади для первого сопоставительного расчета представлены в таблице 3.

Таблица 3. Значения осадки поверхности в центре загруженной площади, полученные аналитическими методами

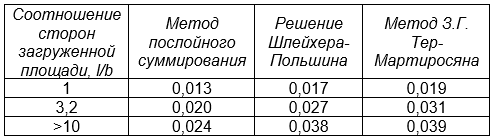
Сопоставление результатов расчета показывает, что классический метод послойного суммирования (с учетом фактического коэффициента невозможности бокового расширения β = 0,74) занижает осадку относительно аналитического решения Шлейхера-Польшина на 24-37%, в зависимости от соотношения сторон фундамента. Это может объясняться как неточностью исходной предпосылки метода о компрессионном режиме сжатия каждого элементарного слоя, так и неизбежной погрешностью, связанной с дискретизацией непрерывной функции изменения напряжений по глубине. Метод З.Г. Тер-Мартиросяна значительно ближе к аналитическому решению – расхождение составляет от 3 до 15%, причем в сторону завышения расчетной осадки (табл. 4). На основании этого сопоставления можно заключить, что метод З.Г. Тер-Мартиросяна больше соответствует фактическому НДС в линейно-упругой среде, однако не учитывает, что интенсивность девиаторной составляющей напряжений в пределах одного элементарного слоя по ширине неодинакова, что и приводит к завышению деформации.

Второй расчет, демонстрирующий практическую реализацию инженерного метода в линейной постановке, учитывал вес основания и более реалистичные геометрические параметры. Результаты расчета приведены в таблице 4.

Таблица 4. Значения осадки поверхности, м, в центре загруженной площади, полученные инженерными и численными методами в линейной постановке

Для предлагаемого нелинейного метода начальные значения модулей приняты по таблице 2, а степенной коэффициент m = n = 0,5. Как и в случае МПС, из компонент напряжений от внешней нагрузки σ_p вычитались соответствующие компоненты бытовых напряжений σ_g.

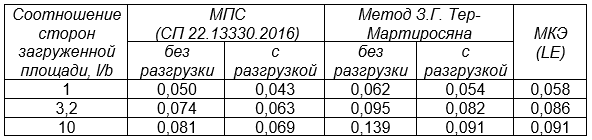
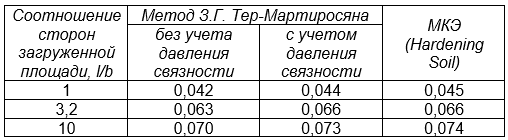
В связи с тем, что в численном расчете для устойчивости решения потребовалось ввести ненулевое значение сцепления, третий сопоставительный расчет был выполнен в двух вариантах – с учетом и без учета давления связности в степенном законе жесткости [9]. Из таблицы 5 видно, что в случае учета давления связности результат расчета практически совпадает с нелинейным численным расчетом.

Таблица 5. Значения осадки поверхности в центре загруженной площади, полученные инженерными и численными методами

В качестве дальнейшего развития метода можно учесть и разгрузку дна котлована. При этом опорное давление p_ref, при котором приняты опорные значения модулей G и К, должно быть не меньше, чем вертикальное бытовое давление σ_zg в уровне дна котлована. В этом случае до достижения данного уровня нагрузки все модули принимаются постоянными величинами, а при превышении его начнут возрастать.

Заключение и обсуждение

В результате сопоставления результатов расчета аналитическими и численными методами в линейно-упругой и нелинейной постановках установлено, что учет сдвиговой деформации наиболее принципиален для фундаментов небольшой ширины. По мере увеличения ширины загруженной площади режим работы каждого элементарного слоя приближается к компрессионному сжатию, и сдвиговая составляющая деформации не вносит существенного вклада в общую осадку, так как размер зон сдвига уменьшается относительно области компрессионного сжатия.

Учет нелинейного изменения жесткости с глубиной уточняет значение осадки и приближает результат расчета к результатам численного моделирования с применением нелинейной модели. При этом результат может быть получен в простой табличной форме без применения специализированного программного обеспечения.

Расхождение предложенного метода в линейной постановке с точным решением Шлейхера-Польшина составляет от 3 до 15%, в то время как для классического МПС – от 24 до 37%, что доказывает корректность выполненных вычислений и полученных значений коэффициентов. В нелинейной постановке метод дает результаты расчета осадки, приближенные к численному решению, и большие, чем МПС, так как учитывает развитие сдвиговых деформаций. Однако учет нелинейной жесткости грунтов приводит к более реалистичной оценке деформации основания.

Предложенный модифицированный метод нелинейного инженерного расчета осадки позволяет:

• учесть зависимость объемной и сдвиговой жесткости от уровня средних напряжений;
• учесть отклонение фактического напряженного состояния от гипотезы о компрессионном сжатии элементарного слоя;
• снизить зависимость результата расчета от выбора мощности сжимаемой толщи.

  ---

Список литературы

1. Тер-Мартиросян З.Г. Механика грунтов. — Москва: АСВ, 2009. — 552 с.

2. Ляв А. Математическая теория упругости. — Ленинград. — ОНТИ, 1935. — 672 с.

3. Короткин В.Г. Объемная задача для упруго-изотропного полупространства // Труды Гидроэнергопроекта. —   1938. —   № 4. —   C. 92-98.

4. Флорин В.А. Основы механики грунтов. Том 1. — Ленинград: Госстройиздат, 1959. — 360 с.

5. Puebla H., Byrne P.M. Analysis of CANLEX liquefaction embankments: prototype and centrifuge models // Canadian Geotechnical Journal. —   1997. —   Т. Can. Geotech. J. 34: 641–657 (1997). —   C. 641-657.

6. Beaty M.H., Byrne P.M. UBCSAND Constitutive model. — Itasca UDM Web Site, 2011.

7. Plaxis Liquefaction Model UBC3D-PLM : / рук. Petalas A., Galavi V., 2013.

8. Galavi V., Petalas A., Brinkgreve R.B.J. Finite element modelling of seismic liquefaction in soils // Geotechnical Engineering Journal of Ihe SEAGS AGSSEA. —   2013. —   Т. 44. —   № 3. —   C. 55-64.

9. Schanz T., Vermeer P.A., Bonnier P.G. The hardening soil model: Formulation and verification // Beyond 2000 in Computational Geotechnics - 10 years of PLAXIS. — Rotterdam: Balkema, 1999. — C. 281-290.

10. Benz T. Small-strain stiffness of soils and its numerical consequences / T. Benz. — Stuttgart, Germany: Institut fur Geotechnik der Universitat Stuttgart, 2007. — 193 с.

11. Schleicher F. Taschenbuch fьr Bauingenieure; Teil: Bd. 1. — Berlin: Springer, 1955. — 1087 с.

12. Польшин Д.Е. Определение напряжения в грунте при загрузке части его поверхности // Труды ВИОС. Основания и фундаменты. —   1933. —   № 1.