Поверхности текучести и законы пластического течения

Очевидно, что ни одно реальное физическое тело не способно деформироваться бесконечно долго и полностью восстанавливать форму после снятия нагрузки. Тем не менее большинство конструкционных материалов, таких как сталь или железобетон, используются при пренебрежимо малых величинах деформаций исключительно в линейно-упругом диапазоне, что позволяет применять к ним теорию упругости. В дисперсных средах пластические деформации преобладают над упругими, что необходимо учитывать при моделировании. Вопросы деформирования тел за пределом упругости рассматривает теория пластичности.

Неограниченное развитие деформаций противоречит гипотезе о малости деформаций (в этом случае перестают выполняться физические уравнения теории упругости) либо приводит к потере сплошности (в этом случае тело разделяется на два отдельных тела, взаимодействующих как механизм). Переход от упругопластического деформирования к неограниченному пластическому течению либо к потере сплошности под действием внешних сил рассматривается теорией прочности.

Если в пространстве главных напряжений отметить все точки, в которых удовлетворяется выбранное условие прочности, то получится некоторая замкнутая поверхность – поверхность прочности. Все точки, попадающие внутрь данной поверхности, соответствуют напряженным состояниям, при которых не превышена прочность материала. Как только траектория изменения напряжений достигает поверхности прочности – «срабатывает» условие прочности – происходит разрушение тела. Традиционно поверхности прочности описываются некоторой функцией прочности, обозначаемой f. При f = 0 точка в пространстве главных напряжений лежит на поверхности прочности.

Поверхности текучести и прочности, помимо пространственного отображения в пространстве главных напряжений, удобно характеризовать посредством меридианного сечения (сечения плоскостью, проходящей по гидростатической оси и оси одного из главных напряжений) и девиаторного сечения (сечения плоскостью, проходящей перпендикулярно гидростатической оси). Пересеченная плоскостью поверхность оставляет на плоскости след. Так, например, след поверхности прочности на девиаторном сечении показывает, как сопротивление разрушению зависит от вида напряженного состояния при постоянном среднем напряжении. След поверхности на меридианной плоскости позволяет оценить влияние среднего напряжения на сопротивление разрушению.

Поверхность прочности хрупких тел разделяет упругое деформирование и нарушение сплошности. Все напряженные состояния внутри поверхности прочности относятся к идеально упругому поведению, а снаружи – хрупкому разрушению (рис. 1, а).

У вязких же тел после упругого деформирования наблюдается развитие пластических деформаций без разрушения (упругопластическая модель). В связи с этим выделяют вторую поверхность, которая разграничивает упругое и пластическое деформирование – поверхность текучести (напомним, что поверхность текучести разграничивает упругое деформирование от пластического течения в идеально упругопластических моделях и от пластического деформирования в упругопластических моделях). Соответственно, траектория напряжений сначала достигает поверхности текучести (и в этот момент деформации перестают быть упругими, начинается развитие пластических деформаций), а затем доходит до поверхности прочности (и в этот момент фиксируется разрушение, то есть полная потеря жесткости, развитие неограниченных пластических деформаций при постоянном напряжении) (рис. 1, в).

Положение поверхности текучести вязкого тела зависит от характера нагружения и особенности деформирования тела. Так, в простых идеально упругопластических моделях поверхность текучести совпадает с поверхностью прочности и отражает переход от упругого деформирования к пластическому течению, минуя при этом стадию пластических деформаций без разрушения (рис. 1, б). Таким образом, все напряженные состояния внутри поверхности текучести относятся к идеально упругому поведению, а снаружи – к неограниченному пластическому течению, то есть разрушению. Следует отметить, что переход деформирования к пластическому течению без стадии пластических деформаций крайне редко наблюдается в реальных телах. Именно поэтому эта модель носит название «идеальной». Подобный тип деформирования характерен для некоторых металлов, которые после превышения предела упругости начинают неограниченно пластически течь.

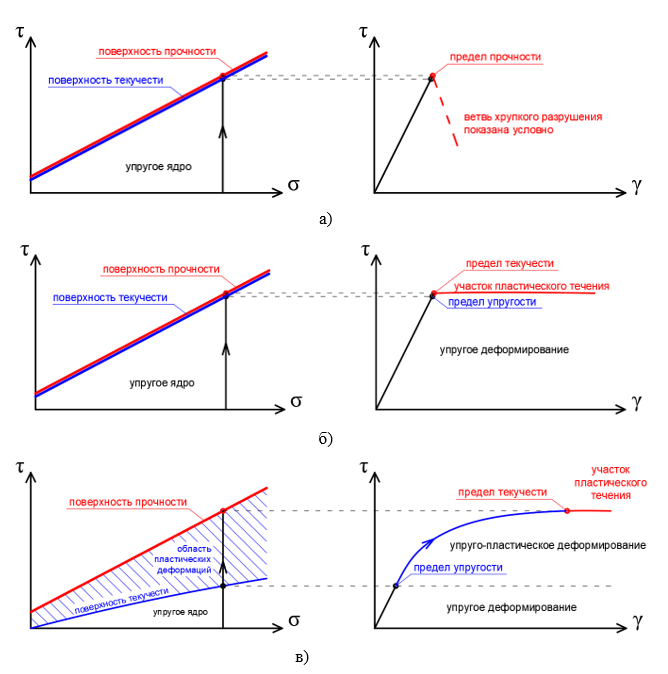
Рис. 1. Следы поверхностей текучести и прочности и графики деформирования: идеально упругопластическая модель в случае хрупкого разрушения (а); идеально упругопластическая модель в случае вязкого разрушения (б); упругопластическая модель с разделенными поверхностями текучести и прочности (в)

Наконец, в моделях с упрочнением/разупрочнением поверхность текучести называют поверхностью нагружения, и она меняет свое положение в зависимости от истории нагружения. Поверхность прочности в данном случае является предельной поверхностью для упрочнения при эволюции поверхности текучести.

Для изотропных тел поверхность прочности будет симметрична относительно гидростатической оси. Но для абсолютного большинства грунтов эта поверхность не является телом вращения, так как предел прочности зависит от вида напряженного состояния. Для структурно-анизотропных тел, в том числе некоторых разновидностей грунтов, ось поверхности прочности не совпадает с гидростатической осью, и в специализированных моделях это учитывается.

Форма поверхности текучести описывается математической функцией, называемой «условием текучести». Ко всем без исключения условиям текучести предъявляются определенные требования, подробнее о которых можно узнать из курса теории пластичности. Данные требования основаны на энергетических принципах описания пластического деформирования.

Постулат Друкера, сформулированный Друкером и Хиллом, состоит из двух утверждений [1, 2]:

- в процессе нагружения увеличение напряжений совершает положительную работу. Так как работа определяется как произведение приращений напряжений и деформаций, это означает, что данные приращения имеют одинаковый знак. С точки зрения физического смысла это утверждение постулирует, что при увеличении напряжений происходит увеличение деформаций;

- за весь цикл дополнительного нагружения и разгрузки добавочные напряжения совершают положительную работу, если имеет место пластическая деформация. Это означает, что сумма работы внешних сил при нагружении и запасенной телом потенциальной энергии, расходуемой на разгрузку, равна нулю при идеально упругом деформировании. Если же совершается пластическая деформация, то часть работы внешних сил расходуется на изменение внутренней энергии тела и сумма работы будет иметь положительный знак (при нагружении потрачено энергии больше, чем запасено телом). Более подробно этот процесс рассматривается в разделе, посвященном гистерезису.

Отсюда следует, что поверхность текучести должна быть выпуклой, то есть луч, выходящий из начала координат, должен пересекать поверхность в единственной точке. Если на поверхности текучести будут «впадины» и «складки», то гипотетически может существовать такая траектория нагружения, при которой снижение напряжений приведет к развитию пластической деформации, а это нарушает закон сохранения энергии (при разгрузке телом будет потрачено больше энергии, чем получено за счет совершения работы внешних сил при нагружении). Отметим, что для разупрочняющихся моделей постулат Друкера не выполняется.

Очевидно также, что поверхность текучести не может проходить через начало координат, так как это означает, что пластические деформации возникают при отсутствии напряжений. Важно учитывать, что данное условие применительно к дисперсным грунтам требует отдельного комментария. Действительно, в твердых телах (и в связных грунтах) за счет наличия жестких связей между элементами структуры любому пластическому деформированию должно предшествовать упругое. Однако для идеально сыпучих сред, не обладающих сцеплением, малейшее увеличение напряжений приводит к пластическому деформированию, что наблюдается в экспериментах и не противоречит физическому смыслу. Тем не менее при численном моделировании это приводит к возникновению пластических деформаций при начальном загружении модели и сразу порождает нелинейное решение.

Именно поэтому в ряде источников встречается рекомендация задавать минимальное значение удельного сцепления, не равным нулю, – в этом случае поверхность текучести не пересекает начало координат и устойчивость численного решения повышается.

Условия текучести и прочности для изотропного материала не должны зависеть от выбора направления осей в системе координат, то есть должны формулироваться в виде функций инвариантов тензора напряжений. Наиболее наглядно это видно на примере хорошо известного условия прочности Кулона – Мора. Закон Кулона сам по себе не может использоваться в расчетах пространственного напряженного состояния, так как связывает между собой нормальные и касательные напряжения на некой опасной площадке, положение которой неизвестно. В то же время закон Кулона – Мора (выраженный уже в главных напряжениях) не зависит от ориентации осей и позволяет оценить прочность на площадках, ориентированных под любым углом.

Теория пластичности предполагает, что всестороннее сжатие/растяжение является исключительно упругим и не должно влиять на положение поверхности текучести (ограничивающей исключительно девиаторное нагружение). Данное требование, как говорилось выше, характерно для сплошных тел, но не относится к дисперсным средам, где всестороннее сжатие может вызывать пластические деформации.

Помимо этих основных требований, есть и дополнительные. Так, например, для использования при численном моделировании желательно, чтобы поверхность текучести в любой точке была дифференцируема, то есть имела бы единственным образом направленную нормаль. Это необходимо, так как направление вектора приращения пластической деформации определяется с помощью касательной к поверхности текучести. Наличие на поверхности текучести складок и ребер приводит к двойственности оценки состояния тела, так как положение касательной плоскости не определено.

Поверхность текучести необязательно должна занимать фиксированное положение в пространстве. Это означает, что история изменения НДС будет вызывать изменение точки перехода от упругого деформирования к пластическому (размер «упругого ядра»). Например, вследствие развития и накопления пластических деформаций после разгрузки и повторного нагружения поверхность текучести будет находиться выше, то есть упругое ядро увеличит размер, произойдет упрочнение (hardening). И наоборот, если при разгрузке поверхность текучести будет уменьшаться вместе с напряжениями – произойдет разупрочнение (softening). Данные процессы позволяют учесть структурные изменения в материале при пластическом деформировании.

Упрочнение при сдвиге больше характерно для дисперсных грунтов с вязким разрушением, в которых развитие пластических деформаций в большинстве случаев приводит к уплотнению скелета и увеличению жесткости и прочности. Разупрочнение, наоборот, встречается в средах с хрупким разрушением, например в скальных грунтах, – накопление дефектов приводит к частичной или полной необратимой потере прочности при многократном нагружении. Также с помощью разупрочнения описывается поведение чувствительных грунтов, сопротивление которых сдвигу снижается вследствие тиксотропии.

Многие зарубежные источники связывают упрочнение и разупрочнение с состоянием переуплотнения. В недоуплотненных и нормально уплотненных грунтах обычно наблюдается достаточно высокая пористость, и при сдвиге происходит уплотнение скелета. При этом образуются новые контакты, и сопротивление дальнейшему сдвигу постепенно возрастает. В переуплотненных грунтах сдвиг вызывает постепенное разрушение контактов и снижение сопротивления сдвигу, за счет чего наблюдается разупрочнение. Данные утверждения можно рассматривать только в общем смысле, так как в природных грунтах возможны различные отклонения от этой закономерности.

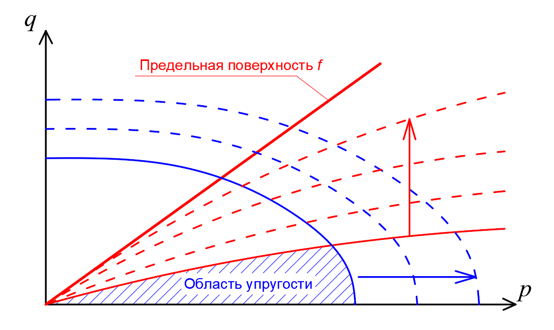
Рис. 2. Сдвиговое (красный цвет) и объемное (синий цвет) упрочнение в плоскости инвариантов p - q на примере модели Hardening Soil

Упрочнение может наблюдаться и при объемном сжатии – это означает, что дальняя точка шатровой поверхности текучести будет отодвигаться от начала координат. Эта важная особенность характерна для всех дисперсных сред: при первичном объемном сжатии в них наблюдаются пластические деформации объема, а при повторном - уже только упругие.

Различают изотропное и кинематическое упрочнение. При изотропном упрочнении поверхность текучести симметрично увеличивается относительно гидростатической оси. Для большинства грунтов характерно именно изотропное упрочнение.

При кинематическом упрочнении размер поверхности текучести не меняется, но ее положение в пространстве главных напряжений смещается, то есть предел упругости изменяется в различных направлениях по-разному. Это характерно для металлов при таких явлениях, как наклеп. Кинематическое упрочнение в дисперсных грунтах также имеет место (например, при переуплотнении глинистых грунтов и формировании анизотропной структуры), но слабо изучено. Тем не менее модели с кинематическим упрочнением используются, например, для расчетов динамической устойчивости грунтов.

Упрочнение (разупрочнение) описывается в каждой модели отдельной функцией – законом упрочнения. В зависимости от используемых в модели решений закон упрочнения может записываться по-разному, однако чаще всего он связывает размер поверхности текучести с уровнем достигнутых напряжений либо пластической деформации. Примеры отдельных законов упрочнения будут приведены в описании конкретных моделей во второй части книги.

Очевидной особенностью всех пластических тел является развитие течения в направлении действия напряжений, вызывающих это течение, – точно так же, как и жидкости текут в направлении градиента сил [3]. Это позволяет связать направление вектора приращения пластической деформации с вектором приращения напряжений.

В теории пластичности сплошного тела предполагается, что при пластическом течении объем тела остается постоянным (то есть объемные деформации равны нулю, объемная жесткость бесконечно велика, а коэффициент Пуассона стремится к 0,5). При этом для материалов, предел упругости которых не зависит от среднего напряжения (например, металлы), можно использовать условия прочности, в которых поверхность прочности параллельна гидростатической оси (например, Мизеса или Треска – Сен-Венана). Исходя из этого, при пластическом течении будут развиваться исключительно деформации сдвига, то есть вектор развития деформаций будет перпендикулярен поверхности текучести (рис. 3, а). Это утверждение носит название «ассоциированного закона пластического течения», так как вектор развития деформаций связан, «ассоциирован» с поверхностью текучести:

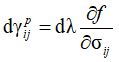
Если же применить ассоциированный закон пластического течения к материалам, предел упругости которых зависит от среднего напряжения (например, дискретным, для которых используются поверхности прочности, непараллельные гидростатической оси), то это приведет к появлению чрезмерно высокого значения объемной составляющей пластической деформации (из-за принятия перпендикулярности вектора деформаций) (рис. 3, б). В реальном эксперименте объемные деформации при сдвиге в данных телах действительно будут наблюдаться, однако их величина будет значительно меньше. Фактически наблюдаемый в эксперименте вектор развития пластических деформаций окажется не перпендикулярен поверхности текучести. В этом случае для оценки пластических деформаций используется еще одна поверхность, перпендикуляр к которой будет соответствовать вектору развития деформаций, – поверхность пластического потенциала. Она не совпадает с поверхностью текучести и описывается отдельной функцией напряжений. Производная от пластического потенциала используется в неассоциированном законе пластического течения.

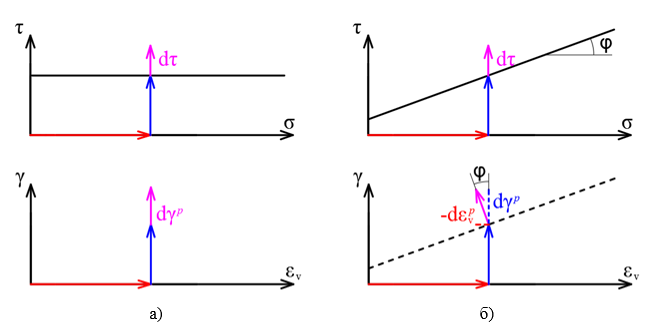
Рис. 3. Применение ассоциированного закона пластического течения для материалов, предел упругости которых не зависит от среднего напряжения (а) и материалов, предел упругости которых зависит от среднего напряжения (б)

В теорию пластического течения Д. Друкером и В. Прагером [4] было введено понятие пластического потенциала. Пластическим потенциалом называется такая функция напряжения g, частная производная от которой пропорциональна приращению пластической деформации:

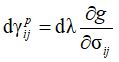
Для условия прочности Кулона – Мора потенциал пластичности g – функция, определяющая направление вектора приращений пластической деформации, – задается группой уравнений:

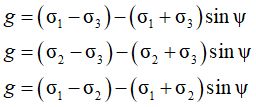
Угол наклона поверхности потенциала пластичности именуется углом дилатансии и обозначается ψ. В целом дилатансией называется свойство дисперсных грунтов изменять объем при сдвиге. Это явление обусловлено переупаковкой частиц при развитии сдвиговых деформаций, что приводит к разуплотнению при изначально плотной упаковке (дилатансии) или уплотнению при изначально рыхлой упаковке (контракции). Соответственно, данные процессы могут сменять друг друга при сложной траектории нагружения. Проявление дилатансии в дисперсных грунтах не позволяет использовать допущение теории пластичности об отсутствии объемных деформаций при пластическом течении.

Угол дилатансии обеспечивает учет изменения объема при развитии пластических деформаций сдвига (контракция при Δε_v < 0 и дилатансия при Δε_v > 0). В ассоциированном законе пластического течения угол дилатансии ψ равен углу внутреннего трения φ, поверхность текучести одновременно рассматривается как потенциальная поверхность (g = f) (рис. 3).

При 0 < ψ << φ используется неассоциированный закон течения - наблюдается дилатансия, происходит увеличение объема (рис. 4, а). При ψ = 0 объемные деформации при сдвиге будут отсутствовать, так как вектор деформаций будет лежать в девиаторной плоскости (рис. 4, б). При ψ < 0 в ходе сдвига объем будет уменьшаться – происходит контракция (рис. 4, в).

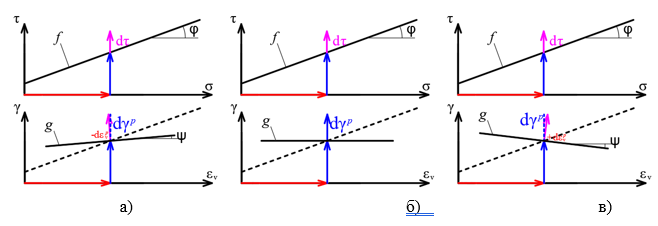
Рис. 4. Неассоциированный закон течения, направление вектора пластической деформации при различных значениях угла дилатансии: ψ > 0 – дилатансия (а); ψ = 0 – пластические объемные деформации отсутствуют (б); ψ < 0 – контракция (в); g – след поверхности пластического потенциала, f – след функции текучести.

Функция пластического потенциала является неотъемлемым атрибутом любой упругопластической модели. Она может быть подобна функции текучести или отличаться от нее. Некоторые программные комплексы предоставляют пользователю возможность независимого выбора формы поверхности пластического потенциала и поверхности текучести.

Для определения направления вектора пластической деформации требуется, чтобы поверхность текучести была дифференцируема в любой точке. В противном случае для напряженных состояний в точках на ребрах поверхности текучести, а также там, где две поверхности пересекают друг друга, возникают точки сингулярности, то есть в них функция не определена или имеет нерегулярное поведение. Это обстоятельство принципиально в первую очередь для численных расчетов, в которых будет наблюдаться ухудшение сходимости. Для описания функции в недифференцируемой точке используется правило Койтера (рис. 5).

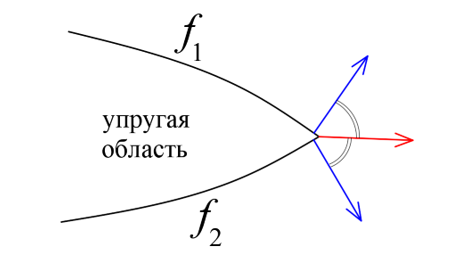
Рис. 5. Реализация правила Койтера в недифференцируемой точке пересечения двух поверхностей текучести. Красным показан результирующий вектор

Принимают, следуя Д. Прагеру [5] и В. Койтеру [6], что течение на ребре является линейной комбинацией течений слева и справа от ребра. Это означает, что вектор пластического течения будет направлен по биссектрисе угла, образованного двумя перпендикулярами к примыкающим поверхностям в ближайших дифференцируемых точках:

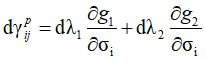
В современных моделях зачастую вводятся дополнительные промежуточные поверхности текучести, обеспечивающие сглаживание поверхности, в связи с чем правило Койтера применять не требуется.

Список литературы

1. Drucker D.C. A definition of a stable inelastic material // Journal of Applied Mechanics. —   1959. —   Т. 26. —   № 1. —   C. 101-195.

2. Hill R. General theory of uniqueness and stability in elastic-plastic solids // Journal of the Mechanics and Physics of Solids. —   1958. —   Т. 6. —   № 3. —   C. 236-249.

3. Schofield A.N., Wroth C.P. Critical State Soil Mechanics. — London: McGraw-Hill, 1968.

4. Drucker D.C., Prager W. Soil mechanics and plastic analysis or limit design // Journal of applied Mathematics. —   1952. —   № 10. —   C. 157-165.

5. Прагер В. Проблемы теории пластичности. — Москва: Физматлит, 1958. — 136 с.

6. Койтер В. Соотношения между напряжениями и деформациями // Механика. —   1960. —   Т. 2.