Описание и параметры моделей А.И. Боткина и Ю.К. Зарецкого

Вероятно, исторически первой моделью, использующей гиперболический закон деформирования, была так называемая «модель А.И. Боткина», основанная на аналитических решениях, опубликованных А.И. Боткиным в конце 30-х – начале 40-х годов XX века [1, 2]. Эти публикации предшествовали значительно более известным в зарубежной литературе работам R. Kondner [3, 4], кроме этого, содержали некоторые решения, позволяющие развить модель с применением положений теории пластичности. Предложенная А.И. Боткиным математическая модель, помимо удачной аппроксимации экспериментально наблюдаемых зависимостей, содержит еще и условие прочности в инвариантной форме. К сожалению, современному специалисту эта модель практически неизвестна и упоминается только в работах отдельных исследователей, например А.Н. Алехина [5]. В данном разделе описание модели приводится на основании публикаций этого автора.

По существу, модель А.И. Боткина является обобщением модели Гука, но с нелинейными значениями модулей объемного сжатия K и сдвига G. Выбор именно этих констант упругости, вместо более привычных модуля общей деформации E и коэффициента относительного поперечного расширения н, представляется значительно более обоснованным для дисперсных грунтов, так как их объемная и сдвиговая жесткость обусловлены принципиально разными механизмами. Объемное сжатие связано с уменьшением объема порового пространства, следовательно, с ростом средних напряжений объемная жесткость возрастает:

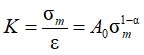
где A₀ – безразмерный параметр, определяющий величину объемной жесткости; σ_m – среднее напряжение; ε – средняя относительная деформация; α – безразмерный параметр степенной функции, близкий по смыслу параметру a в работах N. Janbu [6].

Сдвиговое деформирование сопровождается взаимным смещением частиц скелета и в пределе приводит к разрушению, поэтому по мере накопления дефектов структуры сдвиговая жесткость снижается. В модели А.И. Боткина для этого используется гиперболический закон:

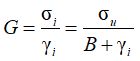
где B – безразмерный параметр, определяющий начальную сдвиговую жесткость; σ_i – интенсивность напряжений; σ_u – предельное значение интенсивности напряжений; γ_i – интенсивность деформаций сдвига.

Предельное напряжение σ_u определяется в соответствии с условием прочности Мизеса – Шлейхера – Боткина.

Следует отметить, что у различных авторов встречаются различные формы записи, не меняющие существа модели, в частности, вместо средних напряжений и деформаций могут использоваться первые инварианты тензора напряжений и деформаций соответственно; вместо интенсивности – вторые инварианты. Эти расхождения в формулировках приводят только к изменениям в величинах коэффициентов модели.

Традиционно математическая модель А.И. Боткина отображается в виде так называемого «паспорта прочности» - диаграммы, включающей в себя ряд зависимостей инвариантов напряжений и деформаций, а также предельную прямую (рис. 1). Это построение объединяет на одной координатной плоскости зависимость между напряжениями, инвариантами напряжений, объемными и сдвиговыми деформациями:

– I квадрант: траектория нагружения, зависимость интенсивности касательных напряжений от среднего напряжения, предельная прямая. Каждый единичный опыт трехосного сжатия отображается в виде траектории нагружения, по предельным точкам можно построить предельную прямую (либо огибающую, если используется нелинейное условие прочности);

– II квадрант: зависимость интенсивности деформаций сдвига от интенсивности касательных напряжений. Для каждого единичного опыта трехосного сжатия могут быть получены свои параметры нелинейного деформирования. Видно, как жесткость меняется с ростом среднего напряжения;

– III квадрант: зависимость интенсивности деформаций сдвига от объемных деформаций, дилатансия и контракция. В этом квадранте каждый опыт трехосного сжатия позволяет получить значение угла дилатансии. Хорошо видно, что с ростом средних напряжений за счет уплотнения скелета грунта дилатансия возрастает. Дальнейшее увеличение среднего напряжения будет, наоборот, приводить к снижению дилатансии, так как объемному расширению будет препятствовать действующее всестороннее давление;

– IV квадрант: зависимость объемных деформаций от среднего напряжения, дилатансия и контракция. В этом квадранте точка окончания консолидации в каждом единичном опыте – это точка на компрессионной кривой, по совокупности опытов ее можно построить полностью. При девиаторном нагружении каждый опыт представляется в виде дополнительного участка зависимости, отражающего дилатансию или контракцию.

Рис. 1. Паспорт прочности грунта (графическое представление модели А.И. Боткина). Цветом выделены зависимости, соответствующие одному опыту; черным показаны зависимости, полученные по совокупности опытов

Насколько известно авторам, в настоящее время модель А.И. Боткина в оригинальном виде не реализована в каких-либо распространенных численных программных комплексах. Тем не менее ее развитие представляется перспективным в связи с простотой и рациональностью используемых зависимостей.

Определение параметров модели А.И. Боткина, учитывая феноменологический характер используемых зависимостей, следут проводить путем подбора значений для достижения наилучшей аппроксимации экспериментальных кривых.

Применительно к крупнообломочным грунтам, используемым в качестве основания и материала гидротехнических сооружений, Ю.К. Зарецким гиперболический закон применялся для описания как объемного, так и сдвигового деформирования. Данная модель во многом напоминает модель А.И. Боткина, но обладает расширенными функциональными возможностями. Модель подробно описана в работах Ю.К. Зарецкого и его учеников [7, 8]. К сожалению, широкого применения модель не нашла, однако, по сведениям авторов, реализована в качестве пользовательской модели в ПК ANSYS и применяется единичными специалистами при проектировании земляных плотин.

В отличие от модели Duncan - Chang для описания жесткости использовался не линейный модуль деформации, а модули сдвига и объемного сжатия. Кроме того, использовались инвариантные величины компонентов НДС – интенсивность касательных напряжений и деформаций сдвига. В результате закон деформирования записывался следующим образом:

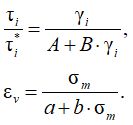
Коэффициенты А, B и a, b предполагалось определять непосредственно по результатам испытаний осесимметричного трехосного сжатия. Интересно отметить, что в данной модели не требуется введения дополнительного закона изменения сдвиговой жесткости от уровня средних напряжений - это происходит автоматически на основании (3), так как увеличение средних напряжений приводит к увеличению предельного значения интенсивности касательных напряжений τ_i*. По существу, кривые деформирования при различных уровнях средних напряжений будут подобны друг другу, как и в моделях, родственных Hardening Soil, но для описания этого требуется существенно более простая запись.

Поверхность прочности в модели описывается модифицированным условием прочности Мизеса – Шлейхера - Боткина и записывается в октаэдрических напряжениях. Поверхность текучести кусочно-линейная, что позволяет хорошо адаптировать модель к фактическим экспериментальным данным. Каждый из участков поверхности текучести соответствует своему виду нагружения: I – объемному растяжению; II – девиаторному нагружению; III - объемному сжатию с девиаторным нагружением; IV – объемному сжатию (рис. 2).

Участок I характеризует поведение материала в области растягивающих напряжений, и за его первую точку принимается «сопротивление отрыву» σ_{m, t}. В качестве упрощения участок I может объединяться с участком II в единую прямую линию, в этом случае поверхность текучести модели примет вид конуса, а начальной точкой линии служит виртуальная точка среднего напряжения, соответствующего давлению связности. Угол наклона этой прямой меняется от начальной величины φ₀ до предельной φ*_oct, текущее значение угла трения φ_oct равнозначно по смыслу мобилизованному углу трения φ_m или углу отклонения θ, но в других координатах – это параметр состояния модели. Отметим также, что Ю.К. Зарецкий в своей монографии «Лекции по современной механике грунтов» приводит также вариант этой модели для различных видов напряженного состояния – при изменении параметра Лоде меняется и форма поверхности текучести. В этом случае форма поверхности текучести в пространстве главных напряжений близка к неправильной шестиугольной пирамиде.

Участки III и IV формируют «шатровую» часть поверхности текучести. Параметром обратного наклона участка III является угол Ψ (не путать с углом дилатансии), начальное значение которого Ψ₀ определяется экспериментально. Пересечение этой прямой с осью абсцисс определяется суммой действующих средних напряжений и структурной прочности. Положение участка IV – вертикальной линии – описывается значением функции упрочнения P*, определяемым в зависимости от накопленной пластической объемной деформации.

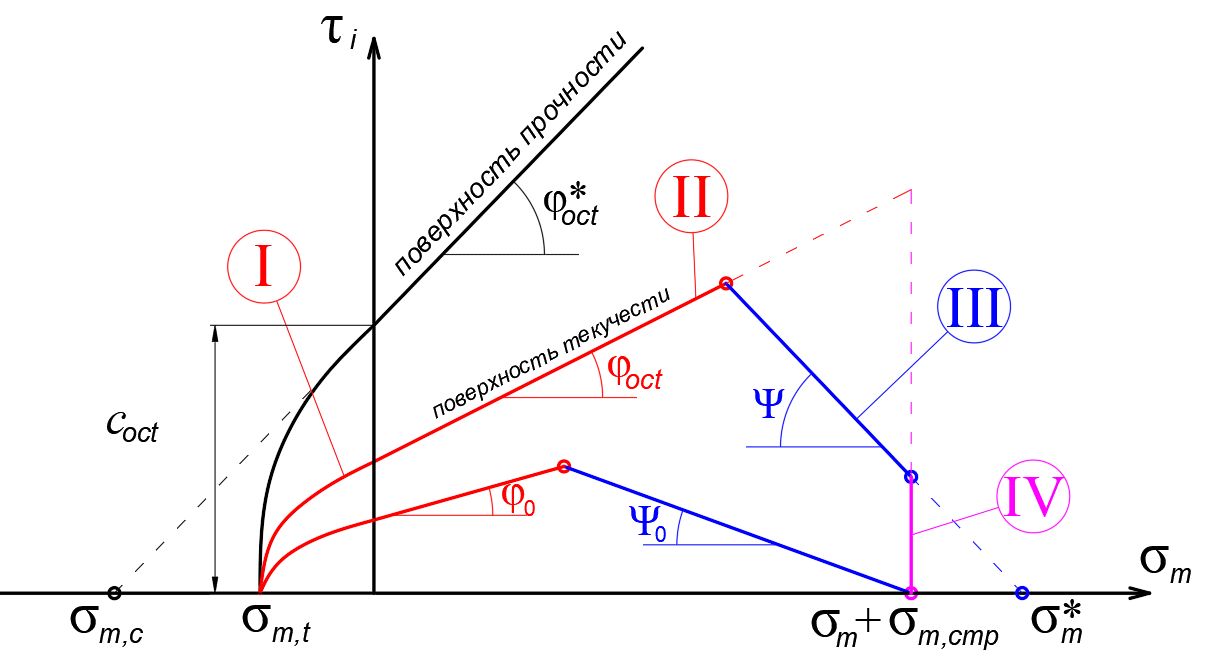
Рис. 2. Поверхности прочности и текучести модели Ю.К. Зарецкого в плоскости «средние напряжения σ – интенсивность касательных напряжений σ_i» [7]

Следует отметить, что выбор конкретных функций и точек раздела участков функции текучести неслучаен – каждый из них обоснован с точки зрения теории накопления и залечивания дефектов структуры дисперсного грунта. В частности, точка пересечения участков III и IV всегда принадлежит траектории CTC при трехосном сжатии в дренированном режиме, что позволяет легко определять ее в любой момент расчета. Участок II предполагает, что пластическая деформация сопровождается разрыхлением (дилатансией), вследствие чего постепенное накопление дефектов структуры не компенсируется залечиванием. Если же нагружение идет по участку III, то за счет уплотнения происходит залечивание накопленных дефектов и такое деформирование может долго не приводить к разрушению.

На рисунке 3 показано направление приращения вектора пластической деформации в различных точках поверхности текучести. Модель использует ассоциированный закон пластического течения. В случае, если нагружение проходит через сингулярную точку, для определения направления вектора течения используется правило Койтера.

Рис. 3. Направление вектора приращения пластической деформации в различных точках поверхности текучести (черный) и его компонент сдвига (красный) и объемного сжатия (синий) в модели Ю.К. Зарецкого [7]

Упрочнение в модели связывает каждую из функций текучести для соответствующих участков поверхности (4) с пластической объемной деформацией, при этом функция упрочнения (Φ, Ψ, P) для каждого участка своя (5). Для упрощения восприятия в выражениях ниже используется система обозначений, принятая ранее в данной монографии.

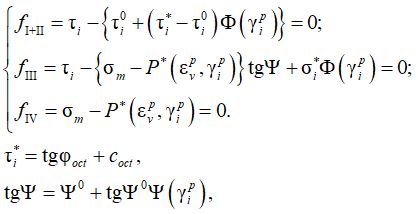
где γ_i^p – интенсивность пластической деформации сдвига; ε_v^p – пластическая объемная деформация; σ_m – среднее напряжение (нормальное октаэдрическое); τ_i, τ_i* - интенсивность касательных напряжений и ее предельное значение соответственно; φ_oct, c_oct – октаэдрические параметры прочности; Φ, Ψ, P – функции упрочнения.

где B – экспериментальный параметр; γ_i* - предельное значение интенсивности пластических деформаций; K^p – модуль объемной пластической деформации.

Максимально подробное описание модели с примером определения параметров на основании паспорта прочности приведено в учебном пособии В.В. Орехова [8].

К безусловным достоинствам модели Ю.К. Зарецкого следует отнести ее простоту и ясный физический смысл каждого параметра, ведь каждое входящее в модель выражение обосновано экспериментальными наблюдениями. В отличие от большинства современных моделей, эта модель может быть полностью определена на основании 3-6 опытов трехосного сжатия, что, собственно говоря, и сделало ее удобным инструментом для проектирования гидротехнических сооружений с применением крупнообломочных грунтов, для которых проведение многочисленных испытаний затруднено, а иногда и невозможно. Несмотря на кажущуюся сложность выражений (4) и (5), математическая постановка модели не требует сложных вычислений.

Таблица. Параметры модели Ю.К. Зарецкого и методы их определения

Список литературы

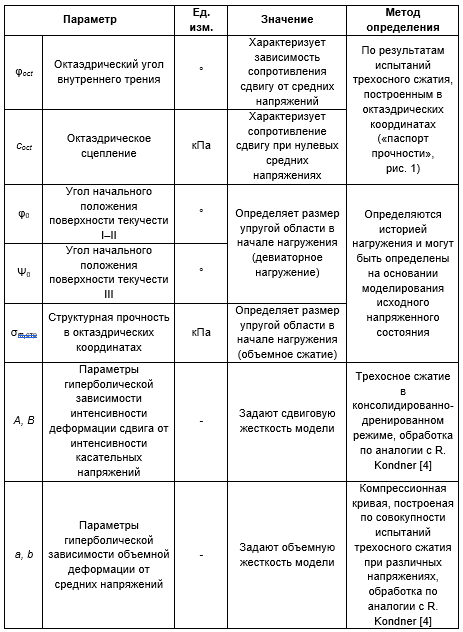
1. Боткин А.И. Исследование напряженного состояния в сыпучих и связных грунтах // Известия ВНИИГ. —   1939. —   № 24. —   C. 153-171.

2. Боткин А.И. О прочности сыпучих и хрупких материалов // Известия ВНИИГ. —   1940. —   Т. 26. —   C. 205-235.

3. Kondner R.L. Hyperbolic Stress-Strain Response: Cohesive Soils // Journal of the Soil Mechanics and Foundations Division, ASCE. —   1963. —   Т. 89. —   № SM1. —   C. 115-143.

4. Kondner R.L., Zelasko J.S. A hyperbolic stress strain formulation for sands // 2 Pan. Am. ICOSFE. — Brazil: 2 Pan. Am. ICOSFE, 1963. — Т. 1. — C. 289-324.

5. Алехин А.Н., Алехин А.А. Эффективный метод определения параметров нелинейной модели грунта из полевых испытаний // Вестник ПНИПУ. Строительство и архитектура. —   2017. —   Т. 8. —   № 4. —   C. 54-63.

6. Janbu N. Soil compressibility as determined by oedometer and triaxial tests // Proc. ECSMFE. — Wiesbaden, 1963. — Т. 1. — C. 19-25.

7. Зарецкий Ю.К. Лекции по современной механике грунтов. — Издательство Ростовского университета, 1989. — 608 с.

8. Орехов В.В. Методика расчетов многофазных, нелинейно деформируемых грунтовых оснований при статических и сейсмических воздействиях. — Москва: МГСУ, 2010. — 80 с.