Как работает программа Plaxis, или Немного о траекториях нагружения
 Федоренко Евгений Владимировичнаучный консультант компании НИП-Информатика, к.г.-м.н., г. Санкт-Петербургeugeniy.fedorenko@nipinfor.ru
Федоренко Евгений Владимировичнаучный консультант компании НИП-Информатика, к.г.-м.н., г. Санкт-Петербургeugeniy.fedorenko@nipinfor.ruОсновной принцип, по которому работают большинство геотехнических программных комплексов (Plaxis, Midas, RS, Z-soil, Гео5 МКЭ, FemModels и др.) заключается в использовании моделей грунта.
Исходные данные
В ходе эволюции математического описания поведения грунтов произошел качественный переход от простых моделей (линейно-упругая и Мор-Кулон) к так называемым усовершенствованным (англ. Constitutivity model). Эти модели представляют собой различные усовершенствования исходной модели CamClay – шатровой с нелинейным поведением при сжатии и увеличением жесткости в условиях компрессионного сжатия – SoftSoil, SoftSoilCreep, HardeningSoil, HardeningSoilSmall, GeneralHardeningSoil (и аналогичные модели с другими названиями в других программах). В основном эти виды моделей используют гиперболическую зависимость при сдвиге и степенную при сжатии.
В геотехнической литературе советского периода авторы периодически обращались к перспективным на то время возможностям численного моделирования, особенно к методу конечных элементов (МКЭ). Использование этого метода на практике требовало серьезных знаний и доступа к сложным ЭВМ. Об этом, например, говорит в «ГеоИнфо» А.Ф. Ким в статье «Ключевые вопросы в отрасли должны решать геотехники». Основным намерением ученых всегда оставалось стремление к совершенствованию математических моделей, описывающих поведение грунта, что прослеживается в работах Ю.К. Зарецкого, С.С. Вялова, А.Б. Фадеева, А.Г. Шашкина и др.
Однако исторически сложившиеся обстоятельства привели к более активному развитию теорий, принятых за рубежом. Особенно этому способствовало более активное развитие компьютерных технологий и появление различных программ (например, Plaxis в 70-х годах прошлого века). Основоположниками этого направления считаются К. Роскоу, А. Скемптон, К. Терцаги и др.
Формирование и развитие усовершенствованных моделей грунта происходило на протяжении длительного периода времени, а основой для этих моделей стала Механика критических состояний грунта (CSSM) о которой в отечественной литературе очень мало упоминаний (А.Б. Фадеев, В.Г. Федоровский, Н.Я. Денисов, перевод на русский язык статьи П. Мэйна). Наверное, можно выделить в механике грунтов отдельное направление, которое включает в себя и нелинейную механику, механику критических состояний и концепцию нормализованных параметров, а назвать это направление, на мой взгляд, можно «геомеханика». Понятие инженерная геомеханика определяет наличие нескольких зависимостей между поведением грунта при различных механических воздействиях, которые объединены в модель грунта, а исходными данными служат не отельные значения абстрактных показателей, а паспорта испытаний грунта в нескольких разных приборах.
Зарождением этого направления можно считать появление в 50-х годах прошлого века математической модели грунта CamClay (модель кембриджской глины) и модели для песков, которые позволили описывать поведение грунтов на более высоком уровне, по сравнению с линейно-упругими и упруго-пластическими моделями типа Linear Elastic и Morh-Columb.
В тоже время усовершенствованные модели грунтов, включенные в коммерческие версии различных геотехнических программ, представляют собой универсальное описание достаточно большого количества вариантов поведения грунтов, но, безусловно, не позволяют точно описывать реальное поведение всего многообразия грунтовых условий. Тем не менее, использование моделей грунта и численного моделирования обеспечивает решение как простых, так и сложных геотехнических задач с более полным анализом (в сравнении с ручным счетом).
Таким образом, с одной стороны, усовершенствованные модели значительно более полно и корректно описывают поведение грунтов по сравнению с ручным счетом, но с другой стороны, являются далеко несовершенными по сравнению с реальным поведением грунтов и для решения разных задач требуют соответствующего выбора той или иной модели. Например, для расчета грунтовых насыпей подходящим вариантом является SoftSoil или SoftSoilCreep; модель для котлованов – HardeningSoil, HardeningSoilSmall, GeneralHardeningSoil; для динамических расчетов есть специальные модели: PM4Sand, UBC3D-PLM, UBCSend и т.д.
Модель грунта так или иначе описывает два основных поведения грунта:
- объемное (изотропное или гидростатическое) сжатие;
- чистый сдвиг (девиаторное нагружение).
Качество описания зависит от вложенных в модель зависимостей и от вводимых исходных данных. Например, модель SoftSoil основана только на компрессионных испытаниях. Следовательно, поведение при сжатии будет хорошо соответствовать поведению образца, а поведение при сдвиге является математической интерпретацией, поскольку в эту модель не вводятся ни трехосные испытания, ни испытания на простой сдвиг. Т.е. к поведению этой модели при преобладании сдвиговых деформаций следует относиться внимательно. Модель HardeningSoil основана на компрессионных и трехосных испытаниях. Соответственно, она более правдоподобно будет описывать и объемные, и сдвиговые деформации, но, конечно, и она не лишена недостатков.
Траектории
Таким образом, введенное в модель поведение лабораторного образца при сжатии и сдвиге, например, в виде независимых модулей одометрического Eoed и трехосного Е50 обрабатывается в ходе моделирования путем построения траекторий нагружения. Стоит отметить, что есть отдельные модели, основанные на полевых испытаниях. Например, модель UBC3D-PLM основана на статическом зондировании SPT и предназначена для учета разжижения грунта при динамическом воздействии.
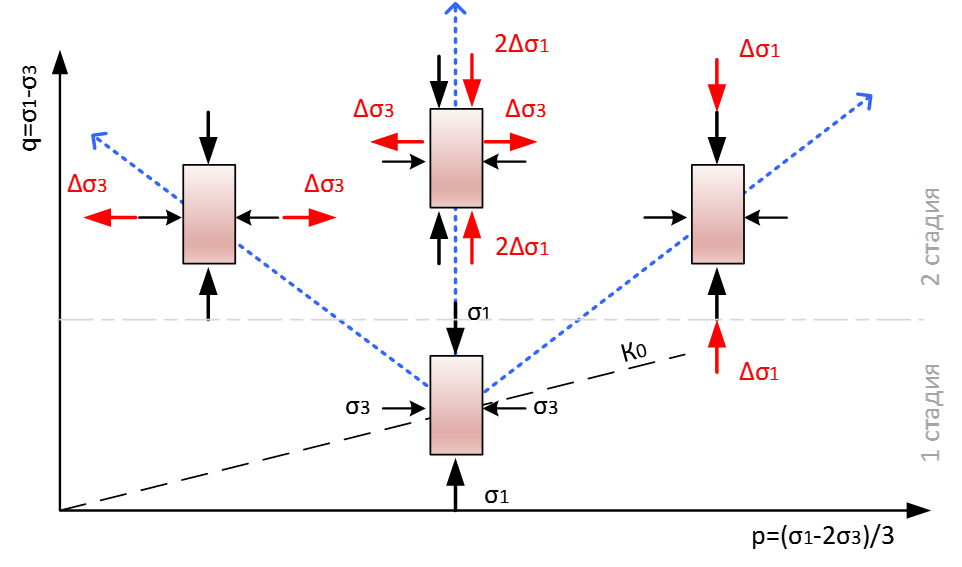
Рассмотрим основные виды траекторий дренированного сжатия для анизотропно нагруженного образца (К0 – консолидация). На рисунке 1 видно, что после первой стадии трехосных испытаний (анизотропное нагружение с вертикальным давлением, превышающим боковое) вторая стадия может происходить тремя путями:
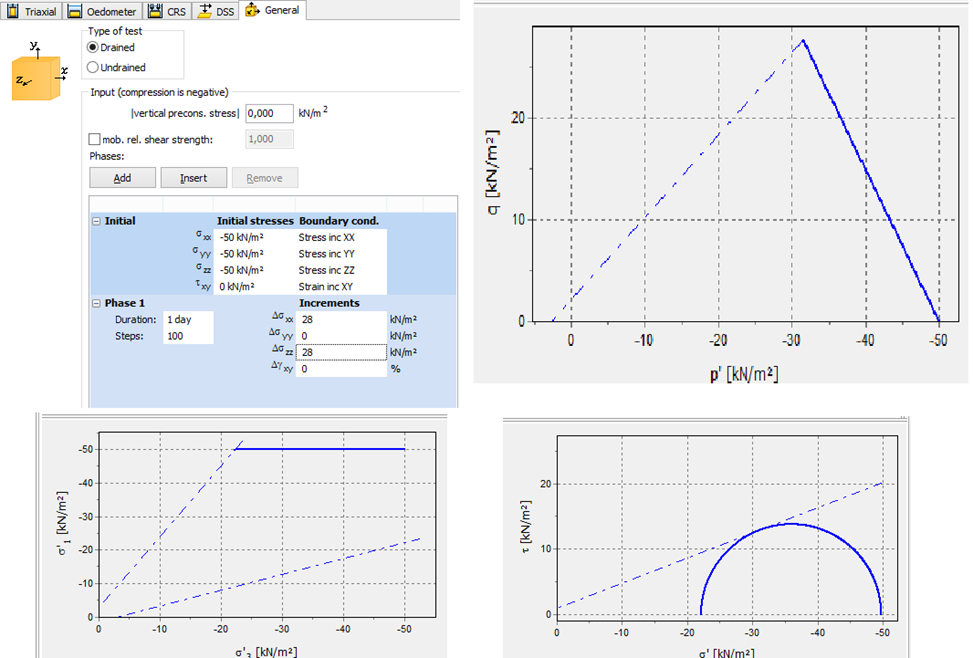
1) снижение бокового давления, при постоянном вертикальном – траектория отклоняется влево;
2) увеличение вертикального давления при одновременном снижении бокового так, чтобы соотношение между ними было постоянным (постоянные касательные напряжения) – вертикальное положение линии (увеличение вертикальной нагрузки равно удвоенному снижению горизонтальной);
3) увеличение только вертикального давления при неизменном боковом – отклонение траектории вправо.
А теперь проиллюстрируем сказанное испытаниями в виртуальной лаборатории SoilTest. Траектории напряжений удобнее смотреть на графике p-q координат.
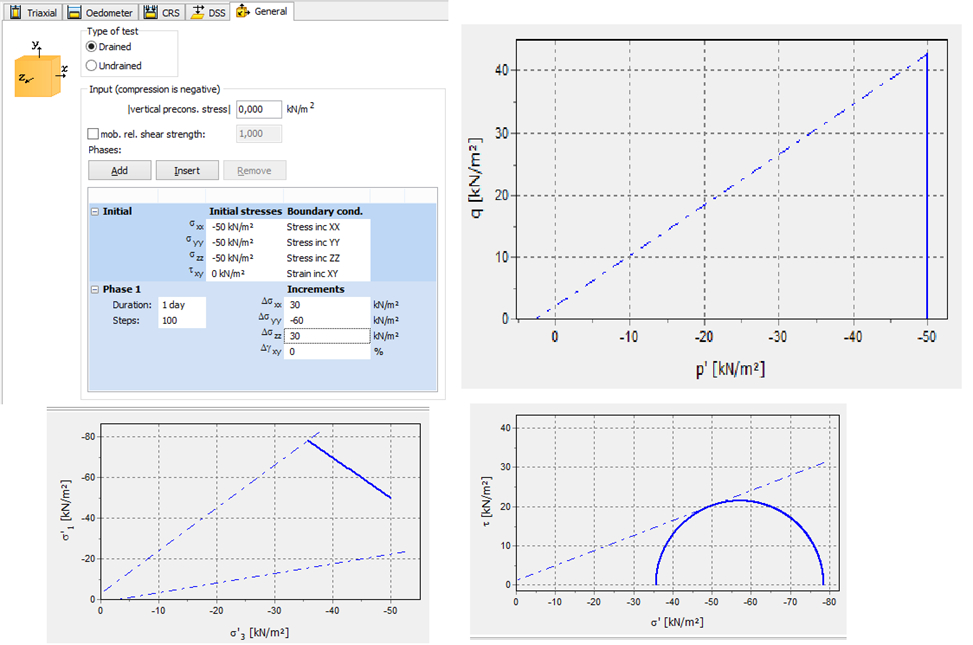
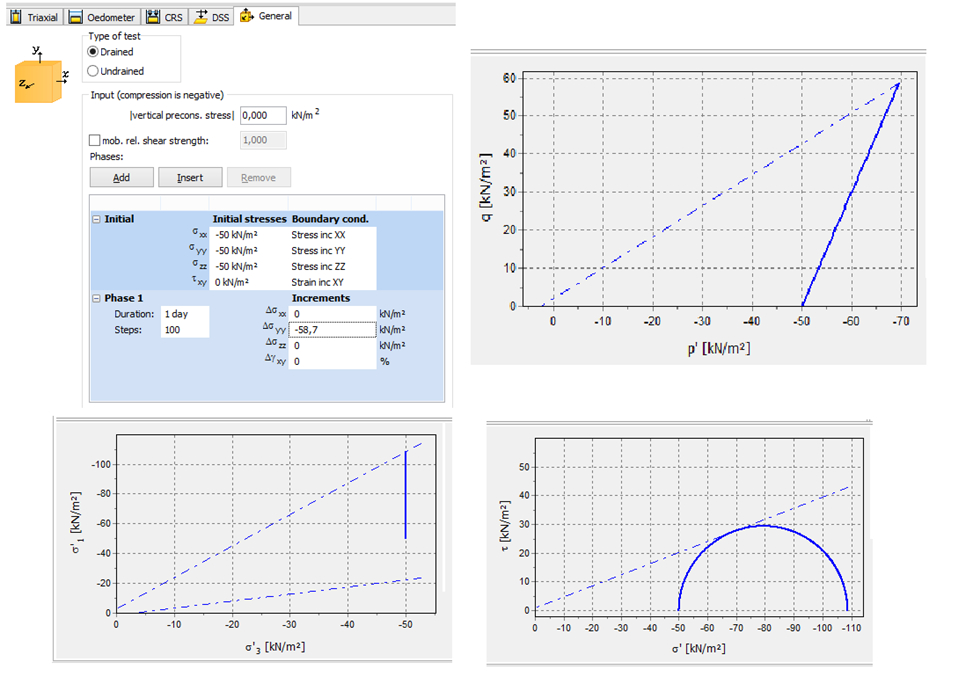
Понимание теории построения траекторий напряжений – необходимое знание для геотехника! Численные методы, в отличие от ручных и инженерных, не дают одного результата, а являются сложным инструментом для анализа нескольких различных параметров расчета.
Пример
Таким образом, при моделировании реальных объектов программа Plaxis делает построение сложных траекторий нагружения в каждой точке каждого конечного элемента и определяет напряженное состояние относительно введённого критерия прочности.
Посмотрим на конкретном примере: стадийное строительство насыпи и последующая откопка котлована. Построим траектории для точки А, расположенной вне зоны компрессионного сжатия насыпи, но в области потенциального смещения при возможных деформациях шпунтовой стенки.
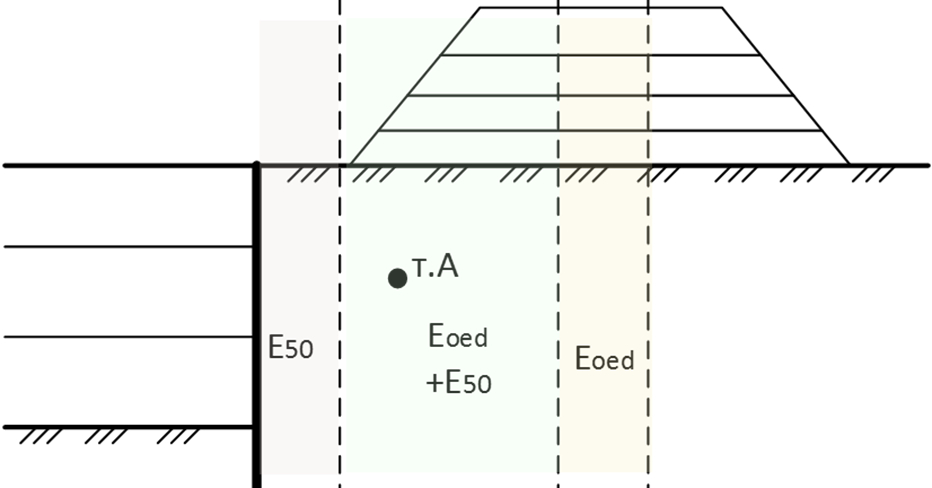
Определяя для каждого момента времени главные эффективные напряжения, получим следующую картину (рис. 6):
начальное напряженное состояние определятся бытовыми вертикальными и горизонтальными напряжениями (зеленый круг);
поэтапная отсыпка насыпи для точки А увеличивает вертикальные напряжения и незначительно – горизонтальные, что приводит к поэтапному смещению круга вправо с увеличением радиуса (серия синих кругов);
откопка котлована после завершения отсыпки насыпи приводит к уменьшению бокового давления при постоянном вертикальном, что проявляется в виде смещения кругов влево с увеличением их радиуса.
Соединяя точки «макушек» кругов получим линию траектории нагружения. Круг, при котором траектория пересечет линию разрушения (критерий прочности), будет определять появление пластической деформации в отдельной рассматриваемой точке (красные точки filure points). Совокупность точек определяет области пластических деформаций и положение поверхности скольжения.
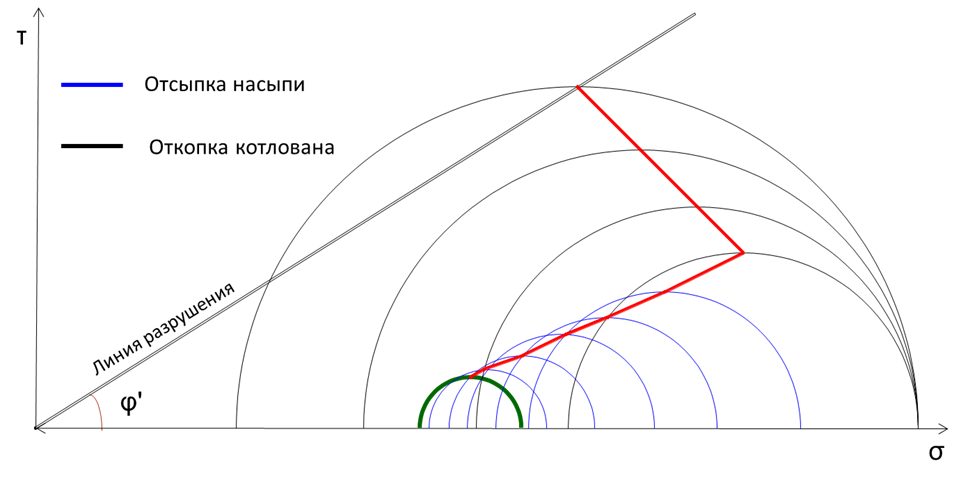
Так выглядит теория.
Теперь сделаем тоже самое путем построения графика траектории нагружения в p-q координатах посредством соответствующего редактора программы Plaxis (рис. 7).
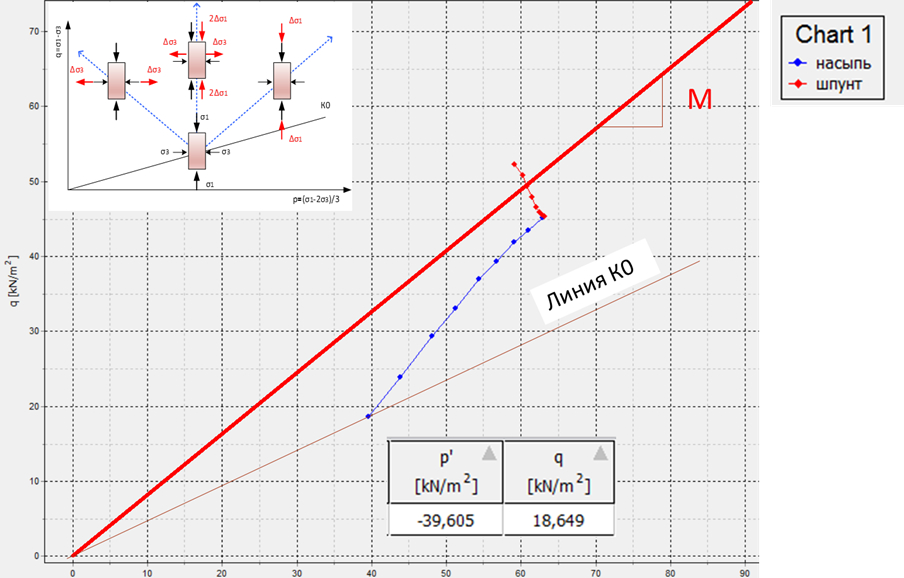
Очевидно, что даже в этом примере в разных точках траектории будут сильно отличаться.
Таким образом, численное моделирование представляет собой сложный процесс определения траекторий нагружения при различных воздействиях с использованием поведения моделей грунта и исходных данных из лабораторных испытаний. Другими словами, задавая простое поведение при сжатии и сдвиге в модель, мы можем получать любые сочетания этих поведений в виде траекторий нагружения при моделировании различных сооружений и процессов.
Для иллюстрации приведем график траекторий нагружения при отсыпке насыпи на водонасыщенные глинистые грунты. Здесь уже используются траектории недренированного нагружения (траектория при отсыпке насыпи отклоняется влево) (подробно это было разобрано здесь) и упрочнение грунта в процессе консолидации.
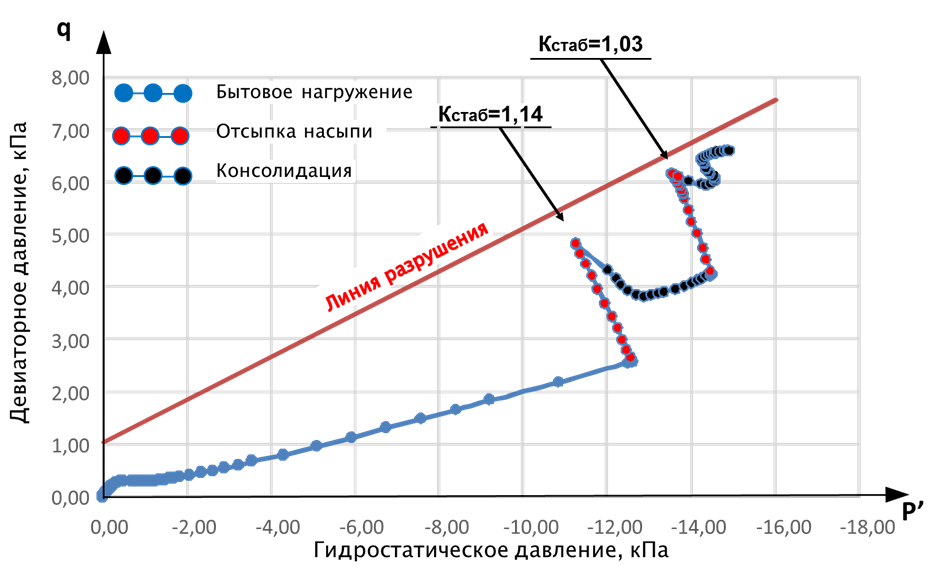
Основное преимущество применения моделей грунта, заключается в том, что при расчетах, например, осадки, учитываются отличия типа приложения нагрузки (фундамент ленточный, столбчатый, плитный и пр.) и вызванных ею пластических деформации. Традиционное использование модуля деформации не позволяет учесть образование и формирование зон пластических деформаций, ведь в штамповых испытаниях они имеют один характер, в компрессионных – другой, а в стабилометрических – третий.














