О программном средстве для практического применения геостатистики в геологии и геотехнике. Часть 3

О КОМПЛЕКСНОЙ СИСТЕМЕ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ДЛЯ ГЕОСТАТИСТИЧЕСКОГО МОДЕЛИРОВАНИЯ В СРЕДЕ PYTHON

GSTools является частью целого набора программных пакетов в системе GeoStat (GeoStat Framework). Они образуют комплексную платформу для геостатистического моделирования на основе языка программирования Python и доступны на сайте веб-сервиса GitHub по адресу github.com/Geostat-Framework. В своей работе [1] Мюллер с соавторами кратко рассказывают о некоторых из этих пакетов и о том, как они взаимодействуют с GSTools, расширяя и усиливая его возможности.

Пакет ogs5py

Программный пакет ogs5py [80] предоставляет API (Application Programming Interface – интерфейс, обеспечивающий взаимодействие программных приложений) на основе Python для конечноэлементного пакета OpenGeoSys 5. Последний используется для научного моделирования гидрогеологических процессов, таких как фильтрационные потоки подземных вод, где типичной проблемой является нехватка данных [81]. Примерами могут служить точечные измерения гидравлического напора в наблюдательных скважинах и кривые, построенные по результатам экспериментов с фильтрацией меченой воды для трассировки ее движения. Для определения коэффициента фильтрации K (коэффициента водопроницаемости K) на основе этих данных требуется система моделирования со стохастической генерацией полей на основе статистических параметров. Комбинированное использование GSTools и ogs5py позволяет пользователю интегрировать геостатистическое моделирование водоносного горизонта с гидрогеологическим моделированием. Пример моделирования испытаний методом опытной откачки подземных вод из скважины будет приведен позже.

Пакеты welltestpy и AnaFlow

Для установления характеристик водоносных горизонтов гидрогеологи обычно используют экономичные испытания методом откачки. Программный пакет welltestpy [82] предоставляет инструменты для обработки, построения графиков и анализа результатов испытаний на откачку. Это помогает практикам определять гидрогеологические параметры путем подбора концептуальной гидродинамической модели к опытным данным. Ряд примеров, иллюстрирующих эти возможности, также приведен в welltestpy.

Пакет AnaFlow [54] предоставляет широкий спектр аналитических формул для испытаний на откачку в различных условиях. Классическими примерами являются решения Тима (Thiem) и Тайса (Theis), в которых принимаются однородные свойства водоносного горизонта. Кроме того, AnaFlow предоставляет расширенные версии обоих этих решений, которые учитывают неоднородность водоносного горизонта и позволяют оценивать геостатистические параметры более высокого порядка, такие как дисперсия и длина корреляции [83, 84].

Пакет PyKrige

GSTools предоставляет интерфейс для автономного пакета PyKrige [85] с более специализированными приложениями для выполнения кригинга. После 10 лет независимого развития PyKrige был перенесен в набор программных средств в системе GeoStat Framework, и теперь его функциональность интегрирована с функциональностью других пакетов данного набора. Пока эти пакеты могут обмениваться между собой ковариационными моделями, но в будущем PyKrige станет инструментом кригинга, включая усовершенствованные методы, для всей платформы GeoStat Framework.

Разработка, хранение, поиск и установка

Пакет GSTools v1.3 совместим со всеми версиями Python начиная с v3.6, хотя предыдущие версии GSTools совместимы с более старыми версиями Python. Критически важные для производительности части, такие как оценка вариограммы, кригинг и рандомизация (описанные в данной статье ранее) реализованы на основе языка программирования Cython, который упрощает написание модулей кода С/С++ для Python, расширяя возможности последнего (код Cython преобразуется в код С/С++ для последующей компиляции и впоследствии может использоваться как расширение стандартного Python или как независимое приложение со встроенной библиотекой выполнения Cython) [86].

GSTools в основном зависит от среды SciPy – библиотеки Python с открытым исходным кодом, позволяющей управлять данными и визуализировать их с помощью высокоуровневых команд и предназначенной для решения научных и математических задач. Библиотека SciPy построена на базе NumPy (также библиотеки Python) [87, 88].

Для оптимизации усилий проектной команды используется GitHub – веб-сервис для хранения и совместной разработки IT-проектов. Пользователи также имеют возможность общаться там с разработчиками, задавая вопросы на дискуссионном форуме, поднимая проблемы или улучшая программы и коды с помощью отправки соответствующих запросов.

Все пакеты поставляются с подробной документацией через сайт-сервис readthedocs.org, содержащий ряд руководств, объясняющих функции программ, и полную документацию по API, созданную с использованием сервера Sphinx.

Система непрерывной интеграции обеспечивается с помощью вкладки GitHub Actions, где для обеспечения простой установки наиболее распространенных операционных систем (Windows, Linux, macOS) встроен современный формат распространения пакетов в среде Python – Python Wheel.

Каждый пакет, выпускаемый на GitHub, попадает в PyPI и conda-forge – каталоги и хранилища программного обеспечения на языке Python (pypi.org; conda-forge.org, [89]), которые помогают находить и устанавливать соответствующие программы и их комплексы.

С помощью GitHub Actions автоматически и непрерывно выполняется обширный набор модульных тестов.

Совместимость программного обеспечения

Чтобы интегрировать GStools в набор пакетов в среде Python, полезных для научных дисциплин (в так называемый научный стек пайтон – Scientific Python Stack), разработчики GStools [1] обеспечили набор интерфейсов для взаимодействия с другими пакетами, такими как рассмотренные ранее ogs5py, meshio, PyVista, а также pyevtk (github.com/pyscience-projects/pyevtk) для операций с сетками.

Поддерживаются и другие пакеты для геостатистики, такие как PyKrige (рассмотренный ранее) и SciKit-GStat [90]. Последний ориентирован на вариографию и может использоваться для более детальной оценки вариограмм. Для обоих этих пакетов предусмотрены интерфейсы для преобразования ковариационных моделей GStools в их аналоги в соответствующем пакете и наоборот.

С точки зрения Мюллера и др. [1], также стоит упомянуть о пакете Verde [91] – библиотеке Python для обработки и привязки пространственных данных к сетке. Некоторые из функций, предоставляемых там, могут быть легко объединены с возможностями инструментов GStools, такими как детрендирование входных данных (удаление тренда) при их предварительной обработке.

НЕКОТОРЫЕ ПРАКТИЧЕСКИЕ ПРИМЕРЫ, ИЛЛЮСТРИРУЮЩИЕ ВОЗМОЖНОСТИ GSTools

Регрессионный кригинг против универсального кригинга: определение температурного тренда в меридиональном направлении

Кригинг – это хорошо зарекомендовавший себя метод интерполяции, применяемый во многих естественнонаучных областях. Мюллер и др. [1] сравнивают два варианта включения вспомогательных переменных для вычисления весов кригинга:

1) с помощью регрессионного кригинга (РК), где тренд входных данных оценивается с помощью регрессии, а к остаткам (residuals – разностям между данными и модельными значениями) применяется простой кригинг;

2) с помощью универсального кригинга (УК), где в качестве внутреннего дрейфа используется модель тренда.

Эти методы различаются по использованию ковариационной модели. Линейный РК не включает информацию о пространственной корреляции, в то время как УК для вычисления весов кригинга использует функцию дрейфа. Часто считается, что оба метода дают математически равные результаты, но Мюллер и др. [1, 92] показывают, что между ними есть ощутимые различия.

В качестве базы данных для исследования на предмет линейного тренда в меридиональном направлении Мюллер и др. [1] использовали значения температуры, измеренные Немецкой метеорологической службой и взятые из такой библиотеки метеорологических служб на основе языка Python, как пакет Wetterdienst [93]. Они применяли устоявшуюся сферическую ковариационную модель в варианте Ядренко, подходящем для географических координат. Оценка вариограммы и результаты подбора модели показаны на рисунке 19.

Рис. 19. Оценка вариограммы температуры с использованием сферической ковариационной модели в варианте Ядренко. Масштаб исследованных расстояний составил примерно 0,9 (в радианах), а порог – около 13 [1]

На рисунках 20 и 21 показаны настройки таких оценивателей, как универсальный кригинг (включая функцию дрейфа) и регрессионный кригинг соответственно. РК требует предшествующего этапа удаления тренда (с помощью подбора регрессионной модели к данным и вычисления разницы между наблюдаемыми и модельными значениями). Результаты интерполяции, показанные на рисунке 22, указывают на то, что оба метода дают одинаково хорошие результаты.

Рис. 20. Настройка универсального кригинга с использованием функции дрейфа [1]

Рис. 21. Настройка регрессионного кригинга с использованием модели линейной регрессии [1]

Рис. 22. Значения температуры воздуха, измеренные в метеорологических будках на высоте 2 м над поверхностью земли (а); результаты интерполяции с помощью универсального кригинга с дрейфом в меридиональном направлении с юга на север (б); результаты интерполяции с помощью регрессионного кригинга с трендом в меридиональном направлении с юга на север (в) [1]

На рисунке 23 представлены оцененные средние тренды как для универсального, так и для регрессионного кригинга. Видно, что они являются совершенно разными. Результаты регрессионного кригинга указывают на рост средней температуры с увеличением широты, что кажется правдоподобным, учитывая понижение уровня земли от Альп на юге к Балтийскому морю на севере. Результаты же универсального кригинга показывают обратное: температура уменьшается с увеличением широты. Потенциальным объяснением здесь является общее снижение температуры при удалении от экватора. В то время как средний тренд для УК лучше соответствует профилю (сечению) по долготе 10° (см. рис. 23), средний тренд для РК лучше соответствует диаграмме рассеяния (как и ожидалось).

Рис. 23. Диаграмма рассеяния «широта – температура» вдоль восточной долготы 10 град.; средний тренд в направлении «юг – север» для регрессионного кригинга; средний дрейф в направлении «юг – север» для универсального кригинга; профили (сечения) соответствующих интерполяций по восточной долготе 10 град. с помощью регрессионного и универсального кригинга [1]

Моделирование фильтрации подземных вод в неоднородном водоносном горизонте

Мюллер и др. [1] указывают, что комбинация программных пакетов ogs5py и GSTools позволяет быстро настраивать и проводить моделирование движения подземных вод в неоднородном водоносном горизонте. Критическим этапом здесь является генерация пространственного распределения проводимости грунта T (водопроводимости, коэффициента водопроводимости), адаптированного к сетке для численного моделирования.

Далее Мюллер и др. [1] демонстрируют способность GSTools генерировать различные структуры взаимодействия и обсуждают их влияние на результаты моделирования на основе базы данных Мюллера и Зеха [94].

Модель движения подземных вод инициализируется с помощью класса OGS пакета ogs5py путем генерации простой сетки (рис. 24) и задания параметров модели и граничных условий. Пространственные случайные поля инициализируются с помощью генератора класса SRF пакета GSTools (рис. 25). Путем передачи подкласса model.msh, передаются детали сетки для генерации распределения значений в определенных местах сетки (даже для неструктурированных сеток). Подпрограмма transform.zinnharvey позволяет генерировать гауссовы системы, в которых средние значения поля не связаны, а области с низкой или высокой водопроницаемостью связаны, используя преобразование Зинна – Харви [76]. Здесь Мюллер и др. [1] обращают внимание на то, что длины корреляции перемасштабируются [95].

Рис. 24. Инициализация модели движения подземных вод с помощью класса OGS пакета ogs5py, начатая с генерации простой сетки [1]

Рис. 25. Генерация коррелированных логарифмически нормальных пространственных случайных полей (в классе SRF пакета GSTools), адаптированных к настройкам сетки численной модели для трех структур связности после преобразования Зинна – Харви [76] [1]

Смоделированные «шлейфы» движения подземных вод, меченых трассирующим индикатором (рис. 26), показывают особые эффекты связности. «Шлейф» остается относительно компактным для классических гауссовых полей, где средние значения связаны. Преобразованные поля приводят к гораздо менее компактным и даже прерывистым динамическим шлейфам, что в основном вызвано торможением или прерыванием фильтрационных потоков подземных вод в связанных областях с низким коэффициентом фильтрации K (низким коэффициентом водопроницаемости K) и преимущественными потоками в связанных областях с высокой водопроницаемостью.

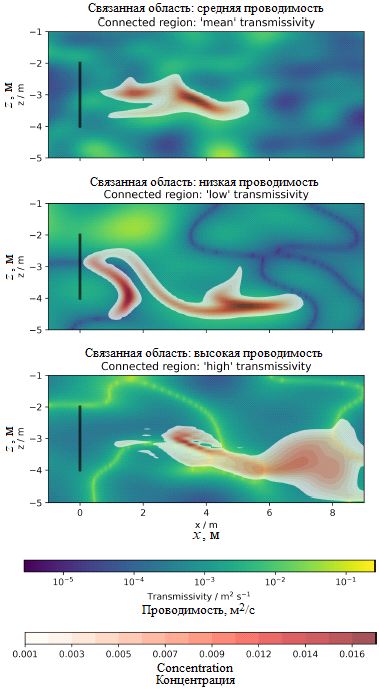
Рис. 26. Результаты моделирования «шлейфов» движения подземных вод, меченых трассирующим индикатором: пространственно-распределенные «шлейфы» концентрации через 15 суток с распределением проводимости T (водопроводимости, коэффициента водопроводимости) на заднем плане [1]

Моделирование опытной откачки

Объединение моделей потоков подземных вод, полученных в пакете программ ogs5py, со случайными полями, сгенерированными в пакете GSTools, позволяет проводить исследования методом Монте-Карло для оценки их среднего поведения в массиве. Зех и др. [84, 96] использовали такой рабочий процесс, чтобы доказать его применимость для моделирования опытных откачек из скважин при случайных значениях проводимости (водопроводимости, коэффициента водопроводимости) грунта. В предложенном ими варианте модель фильтрации подземных вод инициализируется с помощью класса OGS пакета ogs5py с настройкой параметров модели и граничных условий для генерации сходящегося к скважине фильтрационного потока при откачке. Формирование сетки и шаг по времени могут быть специально адаптированы к условиям неравномерного движения потока. Ансамбли гетерогенных полей проводимости генерируются с помощью класса SRF пакета GSTools, где воспроизводимость контролируется начальным (затравочным) значением и где нормальные поля преобразуются на месте с помощью класса normalizer.LogNormal пакета GSTools (рис. 27).

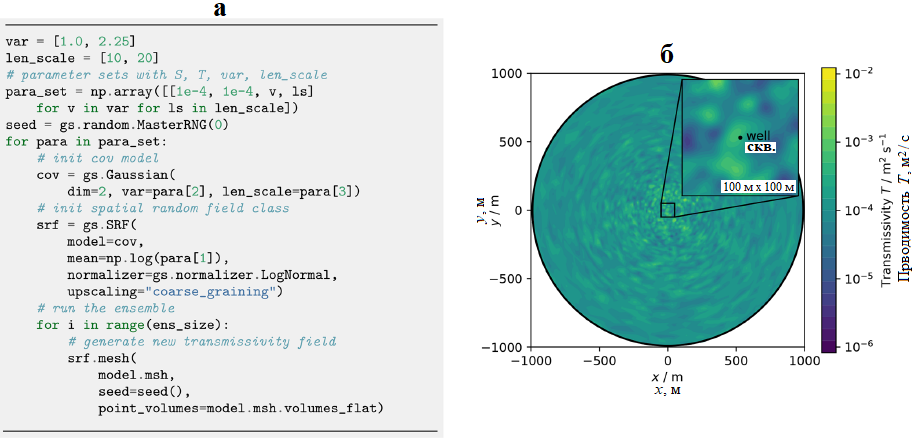
Рис. 27. Последовательность операций для генерации ансамбля полей проводимости T на заданной сетке (a) и одна из реализаций (б) [1]

Использование метода рандомизации (рассмотренного ранее) позволяет адаптировать случайные поля к нерегулярной сетке. Соответствующее увеличение масштаба дисперсии выполняется методом увеличения «зернистости» (уменьшения детализации описания при увеличении масштаба моделирования) для гауссовых вариограмм с использованием уравнения (26), приведенного во второй части.

Рассчитанные средние значения для ансамбля можно сравнить с аналитическими решениями (рис. 28), такими как решение Тейса для однородных сред или решение по эффективному понижению уровня и притоку в скважину [84], используя их реализации в пакетах welltestpy и AnaFlow.

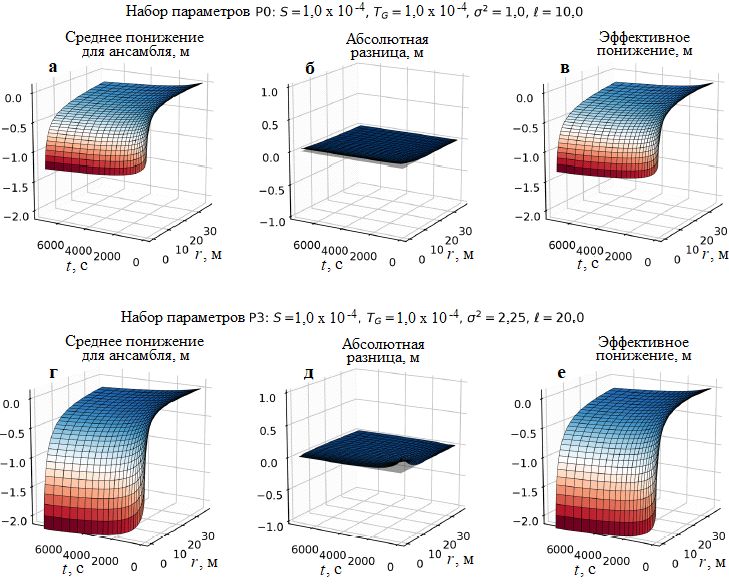
Рис. 28. Сравнение среднего понижения при откачке h(r,t) (а, г) с решением по эффективному напору hCG(r,t) (в, е соответственно) для двух наборов параметров. Исчезающе малая абсолютная разница между ними (б, д соответственно) показывает, что они практически полностью совпадают [1]

Геостатистические тренировочные исследования по водоносному горизонту

Мюллер и др. [1] демонстрируют, как оценивать вариограммы и как обусловливать (определять) пространственные случайные поля по наблюдениям, используя данные для виртуального аналога водоносного горизонта в районе немецкого города Хертен [97]. Этот аналог был сформирован по результатам обследования ряда обнажений гравийного карьера в долине Рейна на юге Германии. 2D-информация (включая гидравлическую, термическую и химическую) была интерполирована в набор 3D-данных. Файлы последовательности операций представлены в работе Шулера и Мюллера [11].

Определяются пространственные корреляции путем оценки вариограммы с помощью функции gstools.variogram. Сначала идентифицируется полная структура проводимости T. Данные по изучаемому аналогу водоносного горизонта приводятся в фациальной структуре (слоях грунта или их группах) с одним значением коэффициента фильтрации K на каждую фацию. Вычисляется проводимость T путем интегрирования коэффициента фильтрации K по вертикальной оси:

Полученное распределение проводимости T, которое показано на рисунке 29, далее принимается за истинное.

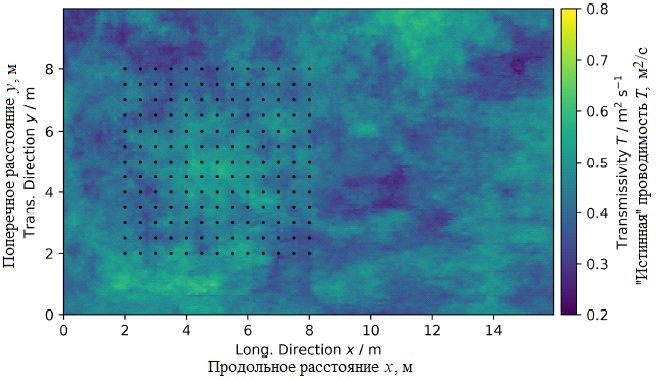
Рис. 29. Пространственное распределение проводимости T виртуального аналога водоносного горизонта города Хертен, принятое за истинное. Черные точки – места виртуальных наблюдений (опорные, или обусловленные, точки) [1]

Выбранные точки наблюдений в количестве 13x13, расположенные по прямоугольной сетке (см. рис. 29), охватывающей подобласть площадью около 42 м², используются для определения эмпирической вариограммы, показанной на рисунке 30. Затем к этим данным подбирается экспоненциальная ковариационная модель, которая с ними хорошо согласуется (с коэффициентом детерминации R² = 0,913).

Рис. 30. Оценка вариограммы (слева), а также полученная экспериментальная (точки) и подобранная модельная (кривая) вариограммы для виртуального аналога водоносного горизонта города Хертен [1]

Далее используется экспоненциальная ковариационная модель, подобранная к эмпирической вариограмме, и ординарный кригинг (Ordinary Kriging) для создания обусловленных пространственных случайных полей в классе CondSRF. На рисунке 31 показана одна из реализаций обусловленного пространственного случайного поля проводимости T и абсолютная разница между «истинной» (см. рис. 29) и обусловленной проводимостью. Разница возрастает по мере удаления от зоны наблюдений (то есть от опорной, или обусловленной, зоны). Эта тенденция еще лучше видна на срезе проводимости на уровне y=4 м, показанном на рисунке 32. Стандартное отклонение, рассчитанное на основе 20 реализаций обусловленных пространственных случайных полей, показывает, что отклонения от обусловленного поля значительно ниже вблизи точек наблюдений.

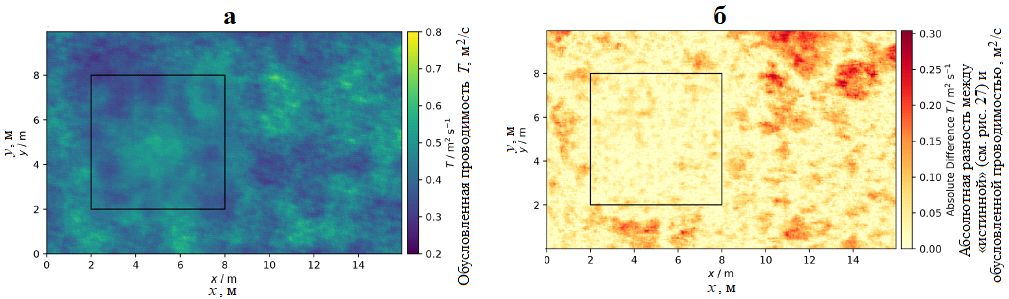
Рис. 31. Одна из реализаций обусловленного пространственного случайного поля проводимости T (a) и абсолютная разница между «истинной» (см. рис. 29) и обусловленной проводимостью, которая показывает увеличение разницы по мере удаления от обусловленной (опорной) зоны, обведенной прямоугольником (б) [1]

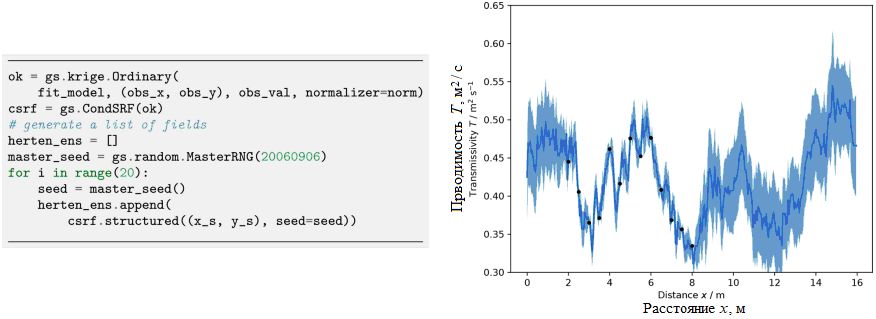
Рис. 32. Генерация ансамбля из 20 обусловленных реализаций и «срез» проводимости T(x) на уровне y=4 м. Жирная синяя линия – «истинная» проводимость (см. рис. 29): окрашенные голубым цветом области – диапазоны в 1 стандартное отклонение, рассчитанные на основе 20 реализаций обусловленных пространственных случайных полей; черные точки – точки наблюдений (опорные, или обусловленные) [1]

ЗАКЛЮЧЕНИЕ

Пакет программ GSTools на основе языка программирования Python предоставляет платформу для геостатистических приложений. Он похож на такие программные пакеты, как gstat на основе языка программирования R или на такие автономные пакеты, как TPROGS [98], GSLIB [26] и S-GeMS [99]. Однако, по мнению Мюллера и др. [1], такой всесторонний и готовый для использования геостатистический программный пакет в среде Python, как GSTools, имеет преимущества просто благодаря выбору языка программирования, который легко освоить и который широко используется в научном сообществе.

Мюллер и др. [1] подчеркивают, что отличительными особенностями GSTools являются возможность генерации в нем случайного поля и его универсальная ковариационная модель. Кроме того, он совместим и интегрирован с другими пакетами на основе Python, такими как PyKrige [85], ogs5py [80] и SciKit-GStat [90], а также предоставляет интерфейсы для пакетов meshio [78] и PyVista [79].

По адресу github.com/GeoStat-Examples можно найти примеры последовательности операций для некоторых задач, которые демонстрируют возможности GSTools и могут служить отправными точками для разработки практиками своих собственных решений геостатистических проблем, с которыми они сталкиваются.

Пакет программ GSTools разрабатывался в рамках системы GeoStat по адресу github.com/GeoStat-Framework/GSTools и доступен по адресу doi.org/10.5281/zenodo.5883346 [34].

GSTools распространяется по лицензии GNU LGPL v3.0.

Документация, которая включает краткое руководство по использованию, несколько подробных руководств и полный обзор по API, доступна по адресу gstools.readthedocs.io/.

Последовательность операций (рабочие процессы) можно найти в отдельных репозиториях по адресам:

• github.com/GeoStat-Examples/gstools-temperature-trend [92];
• github.com/GeoStat-Examples/gstools-connectivity-and-transport [96];
• github.com/GeoStat-Examples/gstools-pumping-test-ensemble [96];
• github.com/GeoStat-Examples/gstools-herten-example [58].

  ---

СПИСОК ЛИТЕРАТУРЫ (REFERENCES)

1. Muller S., Schuler L., Zech A., Hesse F. GSTools v1.3: a toolbox for geostatistical modelling in Python. Geosci. Model Dev. 2022, 15: 3161–3182. doi.org/10.5194/gmd-15-3161-2022. URL: researchgate.net/publication/355409492_GSTools_v13_A_toolbox_for_geostatistical_modelling_in_Python.
2. Krige D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. S. Afr. I. Min. Metall. 1951. 52: 119–139. 
3. Matheron G. Traite de geostatistique appliquee. Editions Technip, 962. 1. 333 .
4. Hohn M.: Geostatistics and Petroleum Geology, computer methods in the geosciences, 2 edn. Springer Netherlands, 1999. doi.org/10.1007/978-94-011-4425-4.
5. Kitanidis P. Introduction to Geostatistics: applications in Hydrogeology, 1st edn. Cambridge University Press, Cambridge, New York., 2008. ISBN 9780521587471.
6. Goovaerts P. Geostatistics in soil science: state-of-the-art and perspectives. Geoderma. 1999. 89: 1–45. doi.org/10.1016/S0016-7061(98)00078-0.
7. Cecinati F., Wani O., Rico-Ramirez M.A. Comparing approaches to deal with non-gaussianity of rainfall data in kriging-based radar-gauge rainfall merging. Water Resour. Res. 2017. 53: 8999–9018. doi.org/10.1002/2016WR020330.
8. Rossi R.E., Mulla D.J., Journel A.G., Franz E.H. Geostatistical tools for modeling and interpreting ecological spatial dependence. Ecol. Monogr. 1992. 62: 277–314. doi.org/10.2307/2937096.
9. Sales M.H., Souza C.M., Kyriakidis P.C., Roberts D.A., Vidal E. Improving spatial distribution estimation of forest biomass with geostatistics: a case study for Rondonia, Brazil. Ecol. Model. 2007. 205: 221–230. doi.org/10.1016/j.ecolmodel.2007.02.033.
10. Monestiez P., Petrenko A., Leredde Y., Ongari B. Geostatistical analysis of three dimensional current patterns in coastal oceanography: application to the gulf of lions (NW Mediterranean sea). In: geoENV IV – Geostatistics for environmental applications, edited by: Sanchez-Vila X., Carrera J., GomezHernandez J.J. Springer Netherlands, Dordrecht, 2004. 367–378. doi.org/10.1007/1-4020-2115-1_31.
11. Schuler L.. Muller, S. GeoStat – examples/gstoolsherten-example: v1.0. Zenodo. 2021. doi.org/10.5281/zenodo.5159658.
12. Kaputin Yu.E., Ezhov A.I., Henli S. Geostatistika v gorno-geologicheskoy praktike [Geostatistics in mining-and-geological practice]. 1995. 165 s. Apatity: KNTs RAN, 1995. 188 s. (in Russian) (Капутин Ю.Е., Ежов А.И., Хенли С. Геостатистика в горно-геологической практике. 1995. 165 с. Апатиты: КНЦ РАН, 1995. 188 с.).
13. Porotov G.S. Matematicheskiye metody modelirovaniya v geologii: uchebnik [Mathematical methods of modeling in Geology: a textbook]. SPb.: Sankt-Peterburgskiy gosudarstvenniy gorniy institut (tekhnicheskiy universitet), 2006. 223 s. (in Russian) (Поротов Г.С. Математические методы моделирования в геологии: учебник. СПб.: Санкт-Петербургский государственный горный институт (технический университет), 2006. 223 с.).
14. Demyanov V.V., Savelyeva E.A. Geostatistika: teoriya i praktika [Geostatistics: theory and practice] / pod red. R.V. Arutyunyana. M.: Nauka, 2010. 327 s. (in Russian) (Демьянов В.В., Савельева Е.А. Геостатистика: теория и практика / под ред. Р.В. Арутюняна. М.: Наука, 2010. 327 с.).
15. Pyrcz M.J., Deutsch C.V. Geostatistical reservoir modeling, 2 edn. Oxford University Press, Oxford, 2014. ISBN 978-0199731442.
16. Rubin Y. Applied Stochastic Hydrogeology, 1st edn. Oxford University Press, New York, 2003. ISBN 9780195138047. doi.org/10.1093/oso/9780195138047.001.0001.
17. Diggle P., Ribeiro P.J. Model-based Geostatistics, Springer Series in Statistics, 1st edn. Springer-Verlag, New York, 2007. doi.org/10.1007/978-0-387-48536-2.
18. Banerjee S., Carlin B.P., Gelfand A.E. Hierarchical modeling and analysis for spatial data, 2 edn. Chapman and Hall/CRC, Boca Raton, 2014.  doi.org/10.1201/b17115.
19. Zhang Y.-K., Zhang D. Forum: the state of Stochastic Hydrology. Stoch. Env. Res. Risk A. 2004. 18: 265. doi.org/10.1007/s00477-004-0190-8.
20. Rajaram H. Debates – Stochastic Subsurface Hydrology from theory to practice: Introduction. Water Resour. Res. 2016. 52: 9215–9217.  doi.org/10.1002/2016WR020066.
21. Neuman S.P. Stochastic groundwater models in practice. Stoch. Env. Res. Risk A. 2004. 18: 268–270. doi.org/10.1007/s00477-004-0192-6.
22. Winter C.L.: Stochastic Hydrology: practical alternatives exist. Stoch. Env. Res. Risk A. 2004. 18: 271–273. doi.org/10.1007/s00477-004-0198-0.
23. Cirpka O.A., Valocchi A.J. Debates – Stochastic Subsurface Hydrology from theory to practice: does stochastic subsurface hydrology help solving practical problems of contaminant hydrogeology? Water Resour. Res. 2016. 52: 9218–9227. doi.org/10.1002/2016WR019087.
24. Fiori A., Cvetkovic V., Dagan G., Attinger S., Bellin A., Dietrich P., Zech A., Teutsch G. Debates – Stochastic Subsurface Hydrology from theory to practice: The relevance of stochastic subsurface hydrology to practical problems of contaminant transport and remediation. What is characterization and stochastic theory good for? Water Resour. Res. 2016. 52: 9228–9234. doi.org/10.1002/2015WR017525.
25. Bellin A., Rubin Y. HYDRO_GEN: a spatially distributed random field generator for correlated properties. Stoch. Hydrol. Hydraul. 1996. 10: 253–278. doi.org/10.1007/BF01581869,
26. Deutsch C.V., Journel A.G.: GSLIB: geostatistical software library and user’s guide, Applied geostatistics series, 2. edn. Oxford University Press, 1997. ISBN 9780195100150.
27. Brouste A., Istas J., Lambert-Lacroix S. On fractional Gaussian random fields simulations. J. Stat. Softw. 2008. 23: 1–23. doi.org/10.18637/jss.v023.i01.
28. Rubin Y., Chen X., Murakami H., Hahn M. A Bayesian approach for inverse modeling, data assimilation, and conditional simulation of spatial random fields. Water Resour. Res. 2010. 46: W10523. doi.org/10.1029/2009WR008799.
29. Pebesma E.J. Multivariable geostatistics in S: the gstat package. Comput. Geosci. 2004. 30: 683–691. doi.org/10.1016/j.cageo.2004.03.012.
30. Savoy H., Hesse F., Rubin Y.: anchoredDistr: a package for the Bayesian inversion of geostatistical parameters with multi-type and multi-scale data. R Journal. 2017. 9: 6–17. doi.org/10.32614/RJ-2017-034.
31. Hesse F., Prykhodko V., Schluter S., Attinger S.: Generating random fields with a truncated power-law variogram: a comprarison of several numerical methods. Environ. Modell. Softw. 2014. 55: 32–48. doi.org/10.1016/j.envsoft.2014.01.013.
32. Vrugt J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Modell. Softw. 2016. 75: 273–316. doi.org/10.1016/j.envsoft.2015.08.013.
33. Rubin Y., Chang C.-F., Chen J., Cucchi K., Harken B., Hesse F., Savoy H. Stochastic hydrogeology’s biggest hurdles analyzed and its big blind spot. Hydrol. Earth Syst. Sci. 2018. 22: 5675–5695. doi.org/10.5194/hess-22-5675-2018.
34. Muller S., Schuler L. GeoStat – framework/GSTools: v1.3.5 “Pure Pink”. Zenodo. January 20, 2022. doi.org/10.5281/zenodo.5883346.
35. Embarak O. Data analysis and visualization using Python analyze data to create visualizations for BI systems, 1st edn. Apress, 2018, 394 р.
36. Rossum G., Dreyk F.L.Dzh., Otkidach D.S., i dr. Yazyk programmirovaniya Python [Python programming language]. 2001, 454 c. URL: script-coding.com/Python/Otkidach.html (Россум, Г., Ф.Л.Дж. Дрейк, Д.С. Откидач и др. Язык программирования Python. 2001, 454 c. URL: script-coding.com/Python/Otkidach.html).
37. Beazley D. Python. Essential Reference, 4th edn. Addison-Wesley, 2010. 860 p. (Бизли Д. Python. Подробный справочник (4-е издание). СПб.: Символ-Плюс, 2010. 864 с. (пер. с англ.)).
38. Buynachev S.K., Boklag N.Yu. Osnovy programmirovaniya na yazyke Python: uchebnoye posobiye [Basics of programming in Python: a tutorial]. Ekaterinburg: Izd-vo Ural'skogo un-ta, 2014. 91 c. (Буйначев С.К., Боклаг Н.Ю. Основы программирования на языке Python: учебное пособие. Екатеринбург: Изд-во Уральского ун-та, 2014. 91 c.).
39. Kovalevskiy E. Geological modelling on the base of Geostatistics. EAGE Student Lecture Tour (SLT), 2011–2012. URL: petroportal.ru/uploads/library/10_4b6fc13e7ef16f780697332a41680c31.pdf (in Russian) (Ковалевский Е. Геологическое моделирование на основе геостатистики. Студенческое лекционное турне EAGE, 2011–2012. URL: petroportal.ru/uploads/library/10_4b6fc13e7ef16f780697332a41680c31.pdf.)
40. Uzielli M., Lacasse S., Nadim F., Phoon K.K. Soil variability analysis for geotechnical practice. Proceedings of the 2nd international workshop on characterisation and engineering properties of natural soils. Singapore, 2006.
41. Isaaks E.H., Srivastava R.M. An Introduction to Applied Geostatistics. Oxford University Press, Inc. New York, 1989. 561 p.
42. Yan-lin S., Ai-ling Z.A., You-bin H., Ke-yan X. 3D geological modeling and its application under complex geological conditions. Procedia Engineering. 2011. 12: 41–46.
43. Kanevskiy M.F., Demyanov V.V., Savelyeva E.A., Chernov S.Yu., Timonin V.A. Elementarnoye vvedeniye v geostatistiku. Problemy okruzhayushchey sredy i prirodnyh resursov. Moskva, VINITI, 1999. 11 (in Russian) (Каневский М.Ф., Демьянов В.В., Савельева Е.А., Чернов С.Ю., Тимонин В.А. Элементарное введение в геостатистику // Проблемы окружающей среды и природных ресурсов. 1999. Москва: ВИНИТИ, 1999. № 11).
44. Bohling G. Introduction to geostatistics and variogram analysis. Kansas Geological Survey, 2005, 1: 1–20.
45. Armstrong M. Geostatistics (in 2 volumes). Kluwer Academic Publishers, 1989. 1027 p.
46. Phoon K.K., Kulhawy F.H. Characterization of geotechnical variability. Canadian Geotechnical Journal. 1999. 36: 612–624.
47. Webster R., Oliver M.A. Geostatistics for environmental scientists, 2d edn. John Wiley & Sons, 2007. ISBN 978-0-470-02858-2.
48. Di Federico V., Neuman S.P. Scaling of random fields by means of truncated power variograms and associated spectra. Water Resour. Res. 1997. 33: 1075–1085. doi.org/10.1029/97WR00299.
49. Wackernagel H. Multivariate Geostatistics: an introduction with applications, 3-d edn. Springer-Verlag, Berlin Heidelberg, 2003. ISBN 978-3-540-44142-7. doi.org/10.1007/978-3-662-05294-5.
50. Rasmussen C.E., Williams C.K. I. Gaussian processes for machine learning, 1st edn. The MIT Press, 2005. ISBN 9780262256834. doi.org/10.7551/mitpress/3206.001.0001.
51. Chiles J.-P., Delfiner P. Geostatistics: modeling spatial uncertainty, 2d edn. Wiley Series in Probability and Statistics (edited by Balding D.J., et al.). John Wiley & Sons, 2012. doi.org/10.1002/9781118136188.
52. Matern B. Spatial variation – stochastic models and their applications to some problems in forest survey sampling investigations. Reports of the Forest Research Institute of Sweden. 1960. 49: 1–144.
53. Wendland H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995. 4: 389–396. doi.org/10.1007/BF02123482.
54. Muller S., Hesse F., Attinger S., Zech A. The extended generalized radial flow model and effective conductivity for truncated power law variograms. Adv. Water Resour. 2021. 156: 104027. doi.org/10.1016/j.advwatres.2021.104027, 2021.
55. Abramowitz M., Stegun I.A. Handbook of mathematical functions, 10th edn. Dover Publications, New York, 1972. ISBN 978-0-486-61272-0.
56. Murray S.G., Poulin F.J.: hankel: a Python library for performing simple and accurate Hankel transformations, The Journal of Open Source Software. 2019. 4: 1397. doi.org/10.21105/joss.01397,
57. Ogata H. A numerical integration formula based on the Bessel functions. Publ. Res I. Math. Sci. 2005. 41: 949–970. doi.org/10.2977/prims/1145474602.
58. Rudin W. Fourier analysis on groups, 1st edn. WileyInterscience, John Wiley & Sons, 1990. ISBN 9780470744819. doi.org/10.1002/9781118165621.
59. Goldstein H. Classical mechanics, 2nd edn. Addison-Wesley, 1980. 672 p. ISBN 9780201029185.
60. Fiori S. A closed-form expression of the instantaneous rotational lurch index to evaluate its numerical approximation. Symmetry. 2019. 11 (10): 1208. doi.org/10.3390/sym11101208.
61. Lantuejoul C., Freulon X., Renard D. Spectral simulation of isotropic Gaussian random fields on a sphere. Math. Geosci. 2019. 51: 999–1020. doi.org/10.1007/s11004-019-09799-4.
62. Sturges H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926. 21: 65–66. doi.org/10.1080/01621459.1926.10502161.
63. Dagan G. Flow and transport in porous formations, 1st edn. Springer, Berlin, Heidelberg, 1989. doi.org/10.1007/978-3-642-75015-1.
64. Eliason S.R.: Maximum likelihood estimation: Logic and practice, 1st edn. Sage Publications. Thousand Oaks, CA, US, 1993. ISBN 9781506315904.
65. Box G.E.P., Cox D.R. An analysis of transformations. J. Roy. Stat. Soc B. 1964. 26: 211–243. doi.org/10.1111/j.2517-6161.1964.tb00553.x.
66. Yeo I., Johnson R.A. A new family of power transformations to improve normality or symmetry. Biometrika. 2000. 87: 954–959. doi.org/10.1093/biomet/87.4.954.
67. John J.A., Draper N.R. An alternative family of transformations. J. Roy. Stat. Soc. C-App. 1980. 29: 190–197. doi.org/10.2307/2986305.
68. Manly B.F.J. Exponential data transformations. J. Roy. Stat. Soc. D-Sta. 1976. 25: 37–42. doi.org/10.2307/2988129.
69. Laekemariam F., Kibret K., Mamo T., Shiferaw H. Accounting spatial variability of soil properties and mapping fertilizer types using geostatistics in southern Ethiopia. Communications in Soil Science and Plant Analysis. 2018. 49 (1): 124–137.
70. Mohammadi H., Riche R.L., Durrande N., Touboul E., Bay X. An analytic comparison of regularization methods for Gaussian processes [preprint]. 5 May 2017. arXiv:1602.00853.
71. Kraichnan R. Diffusion by a random velocity field. Phys. Fluids. 1970. 13: 22–31. doi.org/10.1063/1.1692799.
72. Foreman-Mackey D., Hogg D.W., Lang D., Goodman J. emcee: the MCMC hammer. Publ. Astron. Soc. Pac. 2013. 125: 306–312. doi.org/10.1086/670067.
73. Emery X. Testing the correctness of the sequential algorithm for simulating Gaussian random fields. Stoch. Env. Res. Risk A. 2004. 18: 401–413. doi.org/10.1007/s00477-004-0211-7.
74. Attinger S. Generalized coarse graining procedures for flow in porous media. Computat. Geosci. 2003. 7: 253–273.
75. Schuler L., Suciu N., Knabner P., Attinger S. A time dependent mixing model to close PDF equations for transport in heterogeneous aquifers. Adv. Water Resour. 2016. 96: 55–67. doi.org/10.1016/j.advwatres.2016.06.012.
76. Zinn B., Harvey C.F. When good statistical models of aquifer heterogeneity go bad: a comparison of flow, dispersion, and mass transfer in connected and multivariate Gaussian hydraulic conductivity fields. Water Resour. Res. 2003. 39: 1051. doi.org/10.1029/2001WR001146.
77. Cressie N., Wikle C.K. Statistics for spatio-temporal data. Wiley Series in Probability and Statistics. John Wiley & Sons, Hoboken, New Jersey: 2011. ISBN 978-0-471-69274-4.
78. Schlomer N., McBain G.D., Luu K. et al. nschloe/meshio: None. Zenodo. June 4, 2021. doi.org/10.5281/zenodo.4900671.
79. Sullivan C.B., Kaszynski A.A. PyVista: 3D plotting and mesh analysis through a streamlined interface for the Visualization Toolkit (VTK). Journal of Open Source Software. 2019. 4: 1450. doi.org/10.21105/joss.01450.
80. Muller S., Zech A., Hesse F. ogs5py: a Python – API for the OpenGeoSys 5 Scientific Modeling Package. Groundwater. 2020. 59: 117–122. doi.org/10.1111/gwat.13017.
81. Kolditz O., Bauer S., Bilke L., et al. OpenGeoSys: an open-source initiative for numerical simulation of thermo-hydro-mechanical/chemical (THM/C) processes in porous media. Environ. Earth Sci. 2012. 67: 589–599. doi.org/10.1007/s12665-012-1546-x.
82. Muller S., Leven C., Dietrich P., Attinger S., Zech A. How to find aquifer statistics utilizing pumping tests? Two field studies using welltestpy. Groundwater. 2021. 60: 137–144. doi.org/10.1111/gwat.13121.
83. Zech A., Schneider C.L., Attinger S. The extended Thiem’s solution – including the impact of heterogeneity. Water Resour. Res. 2012. 48: W10535. doi.org/10.1029/2012WR011852.
84. Zech A., Muller S., Mai J., Hesse F., Attinger S. Extending Theis’ solution: using transient pumping tests to estimate parameters of aquifer heterogeneity. Water Resour. Res. 2016. 52: 6156–6170. doi.org/10.1002/2015WR018509.
85. Murphy B., Muller S., Yurchak R. GeoStatFramework/PyKrige: v1.6.0. Zenodo. 2021. doi.org/10.5281/zenodo.4661732.
86. Behnel S., Bradshaw R., Citro C., Dalcin L., Seljebotn D.S., Smith K. Cython: the best of both worlds. Computing in Science Engineering. 2011. 13: 31–39. doi.org/10.1109/MCSE.2010.118.
87. Virtanen P., Gommers R., Oliphan T.E., et al. SciPy1.0: fundamental algorithms for scientific computing in Python. Nat. Methods. 2020. 17: 261–272. doi.org/10.1038/s41592-019-0686-2.
88. Harris C.R., Millman K.J., van der Walt S.J., et al. Array programming with NumPy. Nature. 2020. 585: 357–362. doi.org/10.1038/s41586-020-2649-2.
89. Conda-forge community: the conda-forge project: community based software distribution built on the conda package format and ecosystem. Zenodo. 2015. doi.org/10.5281/zenodo.4774217.
90. Malicke M. SciKit-GStat 1.0: a SciPy-flavored geostatistical variogram estimation toolbox written in Python. Geosci. Model Dev. 2022. 15: 2505–2532. doi.org/10.5194/gmd-15-2505-2022.
91. Uieda L. Verde: processing and gridding spatial data using Green’s functions. Journal of Open Source Software. 2018. 3: 957. doi.org/10.21105/joss.00957.
92. Muller S. GeoStat-Examples/gstools-temperature-trend: v1.0. Zenodo. August 4, 2021. doi.org/10.5281/zenodo.5159728.
93. Gutzmann B., Motl A., Lassahn D., Kamenshchikov I., Bachmann M., Schrammel M. earthobservations/wetterdienst: add units. May 4, 2021. Zenodo. doi.org/10.5281/zenodo.4737739.
94. Muller S., Zech A. GeoStat – Examples/gstoolsconnectivity-and-transport: v1.0. Zenodo. 2021. doi.org/10.5281/zenodo.5159578.
95. Gong R., Haslauer C.P., Chen Y., Luo J. Analytical relationship between Gaussian and transformed-Gaussian spatially distributed fields. Water Resour. Res. 2013. 49: 1735–1740. doi.org/10.1002/wrcr.20143, 2013.
96. Muller S., Zech A. GeoStat – Examples/gstoolspumping-test-ensemble: v1.0, Zenodo. 2021. doi.org/10.5281/zenodo.4891875.
97. Bayer P., Huggenberger P., Renard P., Comunian A. Three-dimensional high resolution fluvio-glacial aquifer analog. Part 1. Field study. J. Hydrol. 2011. 405: 1–9. doi.org/10.1016/j.jhydrol.2011.03.038.
98. Carle S. F. T-PROGS: transition probability geostatistical software, version 2.1. Tech. Rep. University of California, Davis, 1999. URL: gmsdocs.aquaveo.com/t-progs.pdf.
99. Remy N. S-GeMS: the Stanford geostatistical modeling software: a tool for new algorithms development. Geostatistics Banff 2004: Quantitative Geology and Geostatistics. 2005. 14: 865–871. doi.org/10.1007/978-1-4020-3610-1_89.