О программном средстве для практического применения геостатистики в геологии и геотехнике. Часть 2

КРИГИНГ, СЛУЧАЙНЫЕ ПОЛЯ И ОБУСЛОВЛЕННЫЕ СЛУЧАЙНЫЕ ПОЛЯ

Кригинг

Рассматриваемый пакет программ GSTools в своем подпакете gstools.krige имеет подпрограммы для выполнения кригинга – интерполяции методом, при котором интерполированные значения моделируются гауссовым процессом на основе предопределенных ковариационных моделей [49].

Используя интерполяцию данных методом кригинга, можно найти значения параметра в пространстве между его известными значениями. Термин «кригинг» был введен Г. Матероном по фамилии упоминавшегося в первой части статьи южноафриканского горного инженера Дэниела Криге (D. Krige). Этот термин служит для обозначения семейства алгоритмов линейной пространственной регрессии (для регрессионного анализа на основе гауссовых процессов) [14].

Кригинг позволяет учесть вес каждой точки, отображающей экспериментальные данные, в процессе вычисления значений интерполяционной функции в точках регулярной сетки. Это один из наиболее гибких и часто используемых методов, однако для множеств большого размера он работает медленно.

Основная проблема кригинга – необходимость подбора параметров вариограммы, от которых зависит результат интерполяции. На первом этапе вычислений по исходным данным подбирается выборочная (экспериментальная) вариограмма γ*(h) и строится график функции, где каждому интервалу значений h (то есть разности расстояний между парами точек, имеющей размерность в единицах карты – градусах) соответствует вариация (квадрат разности значений в этих точках). При этом h откладывается по оси x или y, а поле принимается изотропным.

Выборочную вариограмму нельзя напрямую использовать в уравнениях кригинга. Ее необходимо приблизить некоторой модельной функцией вариограммы γ(h) (см. таблицу 2), которая используется на втором этапе вычислений.

Данные должны быть нормально распределенными, чтобы влияние выбросов на оценку вариограммы и кригинг было сведено к минимуму. Поэтому вводимые данные оцениваются на предмет нормальности распределения с использованием функции плотности вероятности. Для нормализации распределения данных везде, где это необходимо, выполняется логарифмическое преобразование [6]. Перед кригингом оценивается несколько моделей вариограммы, чтобы выбрать наиболее подходящую для используемого набора данных. Модель наилучшего соответствия выбирается на основе адаптации модели вариограммы, которая точно соответствует экспериментальным значениям и демонстрирует минимальную ошибку (минимальную сумму средних квадратических ошибок) [69]. Согласно работе [13] наилучшим вариантом подобранной модельной функции можно считать тот, который дает наименьшую дисперсию отклонений эмпирических значений от теоретических.

Цель кригинга, как указывают Миллер и др. [1], – получение значений поля z в некоторой точке x₀, когда имеются опорные (обусловленные, определяющие) фиксированные значения z(x₁), ..., z(x_n) в заданных точках x₁, ..., x_n. Результирующее значение z₀ для x₀ вычисляется как средневзвешенное значение

где веса w=(w₁, ..., w_n), определяются конкретной процедурой кригинга.

В подпакете gstools.krige имеется несколько подпрограмм класса Krige – для разных методов кригинга:

1) простого (Simple), когда данные интерполируются с заданным средним значением для поля кригинга;

2) ординарного (Ordinary), когда среднее значение результирующего поля неизвестно и оценивается вместе с интерполяцией;

3) универсального (Universal), когда в дополнение к обычному кригингу подпрограмма может предоставить функции дрейфа f₁, ..., f_k;

4) с внешним дрейфом (ExtDrift), когда процедура подобна универсальному кригингу, но дрейф обеспечивается внешним (external) источником.

Преимуществом использования общего класса Krige является сочетание всех описанных функций, например использование универсального кригинга с функциональным дрейфом вместе с дополнительными внешними дрейфами. Типичным сценарием здесь является,  например, интерполяция температуры с принимаемым дрейфом с севера на юг (функциональным дрейфом) и линейной корреляцией с высотой (внешним дрейфом).

Поскольку во всех моделях вариограмм в GSTools принимается слабая стационарность, система кригинга всегда строится на соответствующей ковариационной функции:

В формуле (23) вектор 1 и его множитель Лагранжа µ приведены в скобках, поскольку их вид зависит от того, должна ли система быть несмещенной или нет (обычный это или простой кригинг). Здесь Мюллер и др. [1] обращают внимание на то, что количество функциональных дрейфов k и внешних дрейфов l может быть равно нулю в зависимости от того, заданы они или нет.

GSTools также предоставляет возможность учитывать дисперсии ошибок измерений  σ_i² для каждой опорной (обусловленной) точки путем корректирования ковариационной матрицы [49]:

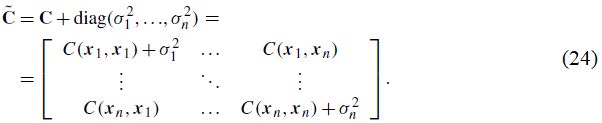
По умолчанию дисперсии ошибок измерений σ_i² установлены по эффекту самородка модели (model nugget). Чтобы получить численно стабильные результаты, решается система кригинга с помощью псевдообратной матрицы, преимущество которой заключается в том, что избыточные данные или множественные измерения в одном и том же месте усредняются в результирующем поле [70].

Последней отмеченной здесь Мюллером и др. [1] особенностью является возможность определения среднего значения [49] с помощью обычного кригинга или оценки среднего дрейфа на основе заданных функциональных и/или внешних условий дрейфа, как показано на рисунке 11. Пример кригинга c линейной интерполяцией показан на рисунке 12.

Рис. 11. Сравнение простого, ординарного и универсального кригинга. Все три подпрограммы имеют схожие настройки, но для простого кригинга требуется оценка среднего значения, а для универсального кригинга дополнительно нужны функции дрейфа. Команды построения графиков опущены [1]

Рис. 12. Простая настройка для линейного регрессионного кригинга. Хотя интерполяция совпадает с кусочно-линейной функцией, мы получаем информацию о дисперсиях ошибок между опорными (обусловленными) точками, как показано на графике [1]

Случайные поля

Основным элементом пакета программ GSTools, как указывают Мюллер и др. [1], является генератор пространственных случайных полей класса SRF (Spatial Random Field). Для реализации пространственного случайного поля необходима ковариационная модель. Предоставляются два способа генерации полей – структурированный и неструктурированный. В обоих случаях позиции (positions), в которых будет оцениваться поле, задаются с помощью аргумента (независимой переменной, параметра) pos. В структурированном случае pos содержит по одному кортежу (набору взаимосвязанных величин или записей) на измерение (dimension), каждый из которых определяет разбиение соответствующей оси, в результате чего получается прямолинейная сетка. Для неструктурированных сеток кортеж pos содержит координаты x, y, z для каждой точки оценки. Класс SRF позволяет управлять базовой генерацией псевдослучайных чисел с помощью начального значения для последующей генерации поля. Пример фрагмента программы приведен на рисунке 13.

Рис. 13. Генерация структурированного случайного поля по гауссовой вариограмме [1]

Генерация поля выполняется с помощью метода рандомизации [31, 70], который использует спектральную плотность (см. уравнение (6)) модели вариограммы для аппроксимации винеровского процесса в пространстве Фурье с помощью следующей формулы:

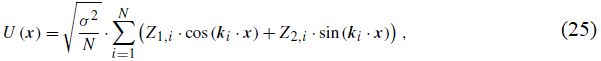
где N – число учитываемых суммируемых членов (мод) ряда Фурье при аппроксимации; Z_1,i, Z_2,i – взаимно независимые cлучайные величины, взятые из стандартного нормального распределения; k_i – взаимно независимые случайные выборки, которые извлекаются из спектральной плотности с помощью модуля emcee пакета Python для генерации выборки методами Монте-Карло по схеме марковских цепей [72].

Метод рандомизации используется по умолчанию в классе RandMeth. Подпрограммы RandMeth создают изотропные случайные поля. Соответствующая ковариация является радиально симметричной, и спектральная плотность может быть вычислена с помощью преобразования Ханкеля. Анизотропия реализуется путем масштабирования и поворота входных точек. Выполняемые процедуры позволяют пользователям генерировать случайное поле только на основе заданной функции корреляции, ковариации или вариограммы.

Ключевым преимуществом применения метода рандомизации является возможность беспроблемного расширения сгенерированного пространственного случайного поля, которое при этом сохраняет не только свои статистические свойства, но и свою фактическую реализацию.

Мюллер и др. [1] перечисляют следующие потенциальные области использования метода рандомизации.

1. Моделирование частиц, при котором случайные несжимаемые поля скоростей могут генерироваться точно в местах расположения отдельных частиц (что будет подробнее рассмотрено в статье позже). Это позволяет избежать ошибок интерполяции, возникающих из-за полей скоростей на основе сетки.

2. Если шлейфы (поля) концентраций моделируются в большой области, пространственное случайное поле может быть рассчитано по запросу только для зависящей от времени пространственной протяженности шлейфа.

3. Для высокопроизводительных вычислительных приложений генерация полей может быть напрямую связана с применением метода декомпозиции (разложения) всей исследуемой области на подобласти, в результате чего для каждой подобласти отдельно решается своя задача генерации пространственного случайного поля.

Мюллер и др. [1] называют также два основных класса методов, альтернативных методу рандомизации [31].

1. Разложив ковариационную функцию, можно очень быстро вычислить небольшие пространственные случайные поля. Но по мере увеличения размера поля вычислительные затраты быстро становятся неосуществимыми.

2. Довольно популярным является метод последовательного гауссова моделирования, с помощью которого также могут создаваться обусловленные пространственные случайные поля. Однако могут возникнуть численные проблемы, если лежащая в основе корреляционная функция является гладкой в начале координат. Кроме того, вычислительные затраты также становятся нецелесообразными или даже неподъемными для случайных полей с высоким разрешением [73].

Так же как и подпрограммы кригинга, генератор пространственных случайных полей класса SRF позволяет включать предопределенные тренды, нормализаторы и средние значения для большего разнообразия распределений. Особенностью этого класса является возможность выполнять масштабирование дисперсии для учета генерации случайных полей в ячейках сетки с определенным объемом. Таким образом, используется метод увеличения «зернистости» (уменьшения детализации описания при увеличении масштаба моделирования) [74], чтобы изменить масштаб дисперсии в уравнении (25) по каждой целевой точке на основе заданного размера фильтра λ:

Этот подход был выведен из уравнения потока грунтовых вод с принятием гауссовой ковариационной модели, поэтому для отличающихся сценариев его следует использовать с осторожностью. Пример будет приведен в данном обзоре позднее.

Обусловленные случайные поля

Мюллер и др. [1] указывают, что при наличии результатов точечных измерений целевой переменной их необходимо учитывать при создании случайных полей. Пакет программ GSTools предоставляет класс CondSRF, объединяющий кригинг и генерацию случайного поля, где сначала получается «кригированное» поле и дисперсия ошибок, а затем генерируется случайное поле с нулевым средним значением, где дисперсия в уравнении (25) заменяется на оцененную дисперсию ошибок. Эта процедура имеет преимущество перед классическим последовательным гауссовым моделированием [47], поскольку:

1) для генерации одного случайного поля используется метод рандомизации;

2) задачу кригинга нужно решить только один раз, а не последовательно.

На рисунке 14 показан пример ансамбля обусловленных случайных полей в одномерной задаче. Там, где доступны измерения целевых переменных, все реализации удовлетворяют им. Однако случайные поля ведут себя как необусловленные поля (то есть как ансамбль с идентичными параметрами, такими как среднее значение, дисперсия и длина корреляции), для которых нет доступных результатов точечных измерений (x>6). Такие характеристики, как дисперсия ансамбля, значительно изменяются с учетом распределения результатов измерений и заданных условий. Среднее по ансамблю и поле кригинга совпадают. Это доказывает, что поле кригинга является наилучшим линейным несмещенным предиктором для заданных данных.

Рис. 14. Пример ансамбля одномерных случайных полей, обусловленных пятью результатами измерений (пятью опорными, или обусловленными, точками). Команды для построения графиков опущены [1]

ДОПОЛНИТЕЛЬНЫЕ ФУНКЦИИ

Генерация несжимаемого векторного случайного поля

Первым, кто предложил метод рандомизации для изучения диффузии одиночных частиц в несжимаемом случайном поле скоростей, был Крайчнан [71]. Он придумал метод рандомизации, который включает в себя проектор (линейный оператор p, действующий в линейном пространстве, или оператор проецирования), обеспечивающий несжимаемость векторного поля.

Как показывают Мюллер и др. [1], используя метод рандомизации (см. формулу (25)) и добавляя проектор p(k_i) к каждому суммируемому члену (моде) ряда, можно получить:

На рисунке 15 представлен пример генерации структурированного несжимаемого случайного векторного поля с помощью экспоненциальной вариограммы.

Рис. 15. Генерация структурированного несжимаемого случайного векторного поля с помощью экспоненциальной вариограммы [1]

Такие особенности, как граничные условия, не могут быть смоделированы с помощью указанного метода, но его можно использовать, например, при моделировании движений в массиве водонасыщенного грунта [75] или для изучения турбулентности открытой воды [71].

Преобразования полей

Мюллер и др. [1] напоминают, что GSTools генерирует гауссовы случайные поля, в то время как реальные данные часто не соответствуют распределению Гаусса. Обычно эта проблема разрешается с помощью трансформации данных. Пакет GSTools обеспечивает выполнение ряда соответствующих преобразований (помимо степенных с помощью подмодуля нормализатора, о котором говорилось ранее), таких как:

1) binary (бинарное);

2) discrete (дискретное);

3) boxcox (Бокса – Кокса) [65];

4) zinnharvey (Зинна – Харви) [76];

5) normal_force_moments (моментов нормальных сил);

6) normal_to_lognormal (от нормального до логнормального);

7) normal_to_uniform (от нормального до равномерного);

8) normal_to_arcsin (от нормального до арксинусного);

9) normal_to_uquad (от нормального до U-квадратичного).

Для создания более сложных сценариев можно последовательно комбинировать разные преобразования (пример показан на рисунке 16). Здесь Мюллер и др. [1] обращают внимание на то, что (в отличие от работы нормализаторов) преобразования не могут быть адаптированы к заданным данным, поэтому выбор самого подходящего из них остается за пользователем.

Рис. 16. Пример логарифмически преобразованного бинарного поля с низкими значениями, которые соединяются путем последовательного применения преобразований zinnharvey (Зинна – Харви), binary (бинарного) и lognormal (логнормального) [1]

Пространственно-временное моделирование

Как указывают Мюллер и др. [1], пространственно-временное моделирование позволяет получить представление о зависящих от времени вероятностных процессах, таких, например, как температура воздуха, атмосферные осадки и соответствующая консолидация грунта, что имеет большое практическое значение. Пакет GSTools предоставляет метрическую пространственно-временную модель [77] для всех ковариационных моделей, дополняя пространственные измерения временным измерением, что приводит к корреляционной модели следующего вида:

Реализация этого в программном пакете GSTools позволяет напрямую включать пространственную анизотропию и вращение в пространственно-временную модель. GSTools также поддерживает использование произвольных пространственных измерений в пространственно-временных моделях. На рисунке 17 представлен пример генерации пространственно-временного случайного поля с одним пространственным измерением.

Рис. 17. Пример рабочего процесса генерации пространственно-временного случайного поля с одним пространственным измерением [1]

Работа с сетками

Чтобы улучшить обработку пространственных случайных полей в качестве входных данных, для решателей моделей на основе уравнений в частных производных (Partial Differential Equations, PDE), таких как метод конечных элементов, GSTools предоставляет интерфейсы для ряда других пакетов программ, таких как meshio [78], PyVista [79] и ogs5py [80]. При использовании meshio или PyVista сгенерированные поля будут немедленно сохранены в содержимом соответствующих сеток. Имеется два варианта создания поля в заданной сетке: либо по точкам (points="points"), либо по центроидам ячеек (points="centroids"), что важно в зависимости от спецификации переменной в численном алгоритме (математической модели). Пример приведен на рисунке 18.

Рис. 18. Генерация пространственных случайных полей на сетках конечных элементов по центроидам ячеек (левое изображение) или по точкам сетки (правое изображение). Команды построения изображений опущены [1]

-

В третьей части статьи, которая будет вскоре опубликована, будут кратко рассмотрены некоторые другие программные пакеты из их набора в среде Python, совместимость этих пакетов с GSTools, а также совместимость GSTools с предыдущими версиями Python. В конце будут приведены некоторые практические примеры и сделано общее заключение.

СПИСОК ЛИТЕРАТУРЫ (REFERENCES)

1. Muller S., Schuler L., Zech A., Hesse F. GSTools v1.3: a toolbox for geostatistical modelling in Python. Geosci. Model Dev. 2022, 15: 3161–3182. doi.org/10.5194/gmd-15-3161-2022. URL: researchgate.net/publication/355409492_GSTools_v13_A_toolbox_for_geostatistical_modelling_in_Python.
2. Krige D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. S. Afr. I. Min. Metall. 1951. 52: 119–139. 
3. Matheron G. Traite de geostatistique appliquee. Editions Technip, 962. 1. 333 .
4. Hohn M.: Geostatistics and Petroleum Geology, computer methods in the geosciences, 2 edn. Springer Netherlands, 1999. doi.org/10.1007/978-94-011-4425-4.
5. Kitanidis P. Introduction to Geostatistics: applications in Hydrogeology, 1st edn. Cambridge University Press, Cambridge, New York., 2008. ISBN 9780521587471.
6. Goovaerts P. Geostatistics in soil science: state-of-the-art and perspectives. Geoderma. 1999. 89: 1–45. doi.org/10.1016/S0016-7061(98)00078-0.
7. Cecinati F., Wani O., Rico-Ramirez M.A. Comparing approaches to deal with non-gaussianity of rainfall data in kriging-based radar-gauge rainfall merging. Water Resour. Res. 2017. 53: 8999–9018. doi.org/10.1002/2016WR020330.
8. Rossi R.E., Mulla D.J., Journel A.G., Franz E.H. Geostatistical tools for modeling and interpreting ecological spatial dependence. Ecol. Monogr. 1992. 62: 277–314. doi.org/10.2307/2937096.
9. Sales M.H., Souza C.M., Kyriakidis P.C., Roberts D.A., Vidal E. Improving spatial distribution estimation of forest biomass with geostatistics: a case study for Rondonia, Brazil. Ecol. Model. 2007. 205: 221–230. doi.org/10.1016/j.ecolmodel.2007.02.033.
10. Monestiez P., Petrenko A., Leredde Y., Ongari B. Geostatistical analysis of three dimensional current patterns in coastal oceanography: application to the gulf of lions (NW Mediterranean sea). In: geoENV IV – Geostatistics for environmental applications, edited by: Sanchez-Vila X., Carrera J., GomezHernandez J.J. Springer Netherlands, Dordrecht, 2004. 367–378. doi.org/10.1007/1-4020-2115-1_31.
11. Schuler L.. Muller, S. GeoStat – examples/gstoolsherten-example: v1.0. Zenodo. 2021. doi.org/10.5281/zenodo.5159658.
12. Kaputin Yu.E., Ezhov A.I., Henli S. Geostatistika v gorno-geologicheskoy praktike [Geostatistics in mining-and-geological practice]. 1995. 165 s. Apatity: KNTs RAN, 1995. 188 s. (in Russian) (Капутин Ю.Е., Ежов А.И., Хенли С. Геостатистика в горно-геологической практике. 1995. 165 с. Апатиты: КНЦ РАН, 1995. 188 с.).
13. Porotov G.S. Matematicheskiye metody modelirovaniya v geologii: uchebnik [Mathematical methods of modeling in Geology: a textbook]. SPb.: Sankt-Peterburgskiy gosudarstvenniy gorniy institut (tekhnicheskiy universitet), 2006. 223 s. (in Russian) (Поротов Г.С. Математические методы моделирования в геологии: учебник. СПб.: Санкт-Петербургский государственный горный институт (технический университет), 2006. 223 с.).
14. Demyanov V.V., Savelyeva E.A. Geostatistika: teoriya i praktika [Geostatistics: theory and practice] / pod red. R.V. Arutyunyana. M.: Nauka, 2010. 327 s. (in Russian) (Демьянов В.В., Савельева Е.А. Геостатистика: теория и практика / под ред. Р.В. Арутюняна. М.: Наука, 2010. 327 с.).
15. Pyrcz M.J., Deutsch C.V. Geostatistical reservoir modeling, 2 edn. Oxford University Press, Oxford, 2014. ISBN 978-0199731442.
16. Rubin Y. Applied Stochastic Hydrogeology, 1st edn. Oxford University Press, New York, 2003. ISBN 9780195138047. doi.org/10.1093/oso/9780195138047.001.0001.
17. Diggle P., Ribeiro P.J. Model-based Geostatistics, Springer Series in Statistics, 1st edn. Springer-Verlag, New York, 2007. doi.org/10.1007/978-0-387-48536-2.
18. Banerjee S., Carlin B.P., Gelfand A.E. Hierarchical modeling and analysis for spatial data, 2 edn. Chapman and Hall/CRC, Boca Raton, 2014.  doi.org/10.1201/b17115.
19. Zhang Y.-K., Zhang D. Forum: the state of Stochastic Hydrology. Stoch. Env. Res. Risk A. 2004. 18: 265. doi.org/10.1007/s00477-004-0190-8.
20. Rajaram H. Debates – Stochastic Subsurface Hydrology from theory to practice: Introduction. Water Resour. Res. 2016. 52: 9215–9217.  doi.org/10.1002/2016WR020066.
21. Neuman S.P. Stochastic groundwater models in practice. Stoch. Env. Res. Risk A. 2004. 18: 268–270. doi.org/10.1007/s00477-004-0192-6.
22. Winter C.L.: Stochastic Hydrology: practical alternatives exist. Stoch. Env. Res. Risk A. 2004. 18: 271–273. doi.org/10.1007/s00477-004-0198-0.
23. Cirpka O.A., Valocchi A.J. Debates – Stochastic Subsurface Hydrology from theory to practice: does stochastic subsurface hydrology help solving practical problems of contaminant hydrogeology? Water Resour. Res. 2016. 52: 9218–9227. doi.org/10.1002/2016WR019087.
24. Fiori A., Cvetkovic V., Dagan G., Attinger S., Bellin A., Dietrich P., Zech A., Teutsch G. Debates – Stochastic Subsurface Hydrology from theory to practice: The relevance of stochastic subsurface hydrology to practical problems of contaminant transport and remediation. What is characterization and stochastic theory good for? Water Resour. Res. 2016. 52: 9228–9234. doi.org/10.1002/2015WR017525.
25. Bellin A., Rubin Y. HYDRO_GEN: a spatially distributed random field generator for correlated properties. Stoch. Hydrol. Hydraul. 1996. 10: 253–278. doi.org/10.1007/BF01581869,
26. Deutsch C.V., Journel A.G.: GSLIB: geostatistical software library and user’s guide, Applied geostatistics series, 2. edn. Oxford University Press, 1997. ISBN 9780195100150.
27. Brouste A., Istas J., Lambert-Lacroix S. On fractional Gaussian random fields simulations. J. Stat. Softw. 2008. 23: 1–23. doi.org/10.18637/jss.v023.i01.
28. Rubin Y., Chen X., Murakami H., Hahn M. A Bayesian approach for inverse modeling, data assimilation, and conditional simulation of spatial random fields. Water Resour. Res. 2010. 46: W10523. doi.org/10.1029/2009WR008799.
29. Pebesma E.J. Multivariable geostatistics in S: the gstat package. Comput. Geosci. 2004. 30: 683–691. doi.org/10.1016/j.cageo.2004.03.012.
30. Savoy H., Hesse F., Rubin Y.: anchoredDistr: a package for the Bayesian inversion of geostatistical parameters with multi-type and multi-scale data. R Journal. 2017. 9: 6–17. doi.org/10.32614/RJ-2017-034.
31. Hesse F., Prykhodko V., Schluter S., Attinger S.: Generating random fields with a truncated power-law variogram: a comprarison of several numerical methods. Environ. Modell. Softw. 2014. 55: 32–48. doi.org/10.1016/j.envsoft.2014.01.013.
32. Vrugt J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Modell. Softw. 2016. 75: 273–316. doi.org/10.1016/j.envsoft.2015.08.013.
33. Rubin Y., Chang C.-F., Chen J., Cucchi K., Harken B., Hesse F., Savoy H. Stochastic hydrogeology’s biggest hurdles analyzed and its big blind spot. Hydrol. Earth Syst. Sci. 2018. 22: 5675–5695. doi.org/10.5194/hess-22-5675-2018.
34. Muller S., Schuler L. GeoStat – framework/GSTools: v1.3.5 “Pure Pink”. Zenodo. January 20, 2022. doi.org/10.5281/zenodo.5883346.
35. Embarak O. Data analysis and visualization using Python analyze data to create visualizations for BI systems, 1st edn. Apress, 2018, 394 р.
36. Rossum G., Dreyk F.L.Dzh., Otkidach D.S., i dr. Yazyk programmirovaniya Python [Python programming language]. 2001, 454 c. URL: script-coding.com/Python/Otkidach.html (Россум, Г., Ф.Л.Дж. Дрейк, Д.С. Откидач и др. Язык программирования Python. 2001, 454 c. URL: script-coding.com/Python/Otkidach.html).
37. Beazley D. Python. Essential Reference, 4th edn. Addison-Wesley, 2010. 860 p. (Бизли Д. Python. Подробный справочник (4-е издание). СПб.: Символ-Плюс, 2010. 864 с. (пер. с англ.)).
38. Buynachev S.K., Boklag N.Yu. Osnovy programmirovaniya na yazyke Python: uchebnoye posobiye [Basics of programming in Python: a tutorial]. Ekaterinburg: Izd-vo Ural'skogo un-ta, 2014. 91 c. (Буйначев С.К., Боклаг Н.Ю. Основы программирования на языке Python: учебное пособие. Екатеринбург: Изд-во Уральского ун-та, 2014. 91 c.).
39. Kovalevskiy E. Geological modelling on the base of Geostatistics. EAGE Student Lecture Tour (SLT), 2011–2012. URL: petroportal.ru/uploads/library/10_4b6fc13e7ef16f780697332a41680c31.pdf (in Russian) (Ковалевский Е. Геологическое моделирование на основе геостатистики. Студенческое лекционное турне EAGE, 2011–2012. URL: petroportal.ru/uploads/library/10_4b6fc13e7ef16f780697332a41680c31.pdf.)
40. Uzielli M., Lacasse S., Nadim F., Phoon K.K. Soil variability analysis for geotechnical practice. Proceedings of the 2nd international workshop on characterisation and engineering properties of natural soils. Singapore, 2006.
41. Isaaks E.H., Srivastava R.M. An Introduction to Applied Geostatistics. Oxford University Press, Inc. New York, 1989. 561 p.
42. Yan-lin S., Ai-ling Z.A., You-bin H., Ke-yan X. 3D geological modeling and its application under complex geological conditions. Procedia Engineering. 2011. 12: 41–46.
43. Kanevskiy M.F., Demyanov V.V., Savelyeva E.A., Chernov S.Yu., Timonin V.A. Elementarnoye vvedeniye v geostatistiku. Problemy okruzhayushchey sredy i prirodnyh resursov. Moskva, VINITI, 1999. 11 (in Russian) (Каневский М.Ф., Демьянов В.В., Савельева Е.А., Чернов С.Ю., Тимонин В.А. Элементарное введение в геостатистику // Проблемы окружающей среды и природных ресурсов. 1999. Москва: ВИНИТИ, 1999. № 11).
44. Bohling G. Introduction to geostatistics and variogram analysis. Kansas Geological Survey, 2005, 1: 1–20.
45. Armstrong M. Geostatistics (in 2 volumes). Kluwer Academic Publishers, 1989. 1027 p.
46. Phoon K.K., Kulhawy F.H. Characterization of geotechnical variability. Canadian Geotechnical Journal. 1999. 36: 612–624.
47. Webster R., Oliver M.A. Geostatistics for environmental scientists, 2d edn. John Wiley & Sons, 2007. ISBN 978-0-470-02858-2.
48. Di Federico V., Neuman S.P. Scaling of random fields by means of truncated power variograms and associated spectra. Water Resour. Res. 1997. 33: 1075–1085. doi.org/10.1029/97WR00299.
49. Wackernagel H. Multivariate Geostatistics: an introduction with applications, 3-d edn. Springer-Verlag, Berlin Heidelberg, 2003. ISBN 978-3-540-44142-7. doi.org/10.1007/978-3-662-05294-5.
50. Rasmussen C.E., Williams C.K. I. Gaussian processes for machine learning, 1st edn. The MIT Press, 2005. ISBN 9780262256834. doi.org/10.7551/mitpress/3206.001.0001.
51. Chiles J.-P., Delfiner P. Geostatistics: modeling spatial uncertainty, 2d edn. Wiley Series in Probability and Statistics (edited by Balding D.J., et al.). John Wiley & Sons, 2012. doi.org/10.1002/9781118136188.
52. Matern B. Spatial variation – stochastic models and their applications to some problems in forest survey sampling investigations. Reports of the Forest Research Institute of Sweden. 1960. 49: 1–144.
53. Wendland H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995. 4: 389–396. doi.org/10.1007/BF02123482.
54. Muller S., Hesse F., Attinger S., Zech A. The extended generalized radial flow model and effective conductivity for truncated power law variograms. Adv. Water Resour. 2021. 156: 104027. doi.org/10.1016/j.advwatres.2021.104027, 2021a.
55. Abramowitz M., Stegun I.A. Handbook of mathematical functions, 10th edn. Dover Publications, New York, 1972. ISBN 978-0-486-61272-0.
56. Murray S.G., Poulin F.J.: hankel: a Python library for performing simple and accurate Hankel transformations, The Journal of Open Source Software. 2019. 4: 1397. doi.org/10.21105/joss.01397,
57. Ogata H. A numerical integration formula based on the Bessel functions. Publ. Res I. Math. Sci. 2005. 41: 949–970. doi.org/10.2977/prims/1145474602.
58. Rudin W. Fourier analysis on groups, 1st edn. WileyInterscience, John Wiley & Sons, 1990. ISBN 9780470744819. doi.org/10.1002/9781118165621.
59. Goldstein H. Classical mechanics, 2nd edn. Addison-Wesley, 1980. 672 p. ISBN 9780201029185.
60. Fiori S. A closed-form expression of the instantaneous rotational lurch index to evaluate its numerical approximation. Symmetry. 2019. 11 (10): 1208. doi.org/10.3390/sym11101208.
61. Lantuejoul C., Freulon X., Renard D. Spectral simulation of isotropic Gaussian random fields on a sphere. Math. Geosci. 2019. 51: 999–1020. doi.org/10.1007/s11004-019-09799-4.
62. Sturges H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926. 21: 65–66. doi.org/10.1080/01621459.1926.10502161.
63. Dagan G. Flow and transport in porous formations, 1st edn. Springer, Berlin, Heidelberg, 1989. doi.org/10.1007/978-3-642-75015-1.
64. Eliason S.R.: Maximum likelihood estimation: Logic and practice, 1st edn. Sage Publications. Thousand Oaks, CA, US, 1993. ISBN 9781506315904.
65. Box G.E.P., Cox D.R. An analysis of transformations. J. Roy. Stat. Soc B. 1964. 26: 211–243. doi.org/10.1111/j.2517-6161.1964.tb00553.x.
66. Yeo I., Johnson R.A. A new family of power transformations to improve normality or symmetry. Biometrika. 2000. 87: 954–959. doi.org/10.1093/biomet/87.4.954.
67. John J.A., Draper N.R. An alternative family of transformations. J. Roy. Stat. Soc. C-App. 1980. 29: 190–197. doi.org/10.2307/2986305.
68. Manly B.F.J. Exponential data transformations. J. Roy. Stat. Soc. D-Sta. 1976. 25: 37–42. doi.org/10.2307/2988129.
69. Laekemariam F., Kibret K., Mamo T., Shiferaw H. Accounting spatial variability of soil properties and mapping fertilizer types using geostatistics in southern Ethiopia. Communications in Soil Science and Plant Analysis. 2018. 49 (1): 124–137.
70. Mohammadi H., Riche R.L., Durrande N., Touboul E., Bay X. An analytic comparison of regularization methods for Gaussian processes [preprint]. 5 May 2017. arXiv:1602.00853.
71. Kraichnan R. Diffusion by a random velocity field. Phys. Fluids. 1970. 13: 22–31. doi.org/10.1063/1.1692799.
72. Foreman-Mackey D., Hogg D.W., Lang D., Goodman J. emcee: the MCMC hammer. Publ. Astron. Soc. Pac. 2013. 125: 306–312. doi.org/10.1086/670067.
73. Emery X. Testing the correctness of the sequential algorithm for simulating Gaussian random fields. Stoch. Env. Res. Risk A. 2004. 18: 401–413. doi.org/10.1007/s00477-004-0211-7.
74. Attinger S. Generalized coarse graining procedures for flow in porous media. Computat. Geosci. 2003. 7: 253–273.
75. Schuler L., Suciu N., Knabner P., Attinger S. A time dependent mixing model to close PDF equations for transport in heterogeneous aquifers. Adv. Water Resour. 2016. 96: 55–67. doi.org/10.1016/j.advwatres.2016.06.012.
76. Zinn B., Harvey C.F. When good statistical models of aquifer heterogeneity go bad: a comparison of flow, dispersion, and mass transfer in connected and multivariate Gaussian hydraulic conductivity fields. Water Resour. Res. 2003. 39: 1051. doi.org/10.1029/2001WR001146.
77. Cressie N., Wikle C.K. Statistics for spatio-temporal data. Wiley Series in Probability and Statistics. John Wiley & Sons, Hoboken, New Jersey: 2011. ISBN 978-0-471-69274-4.
78. Schlomer N., McBain G.D., Luu K. et al. nschloe/meshio: None. Zenodo. June 4, 2021. doi.org/10.5281/zenodo.4900671.
79. Sullivan C.B., Kaszynski A.A. PyVista: 3D plotting and mesh analysis through a streamlined interface for the Visualization Toolkit (VTK). Journal of Open Source Software. 2019. 4: 1450. doi.org/10.21105/joss.01450.
80. Muller S., Zech A., Hesse F. ogs5py: a Python – API for the OpenGeoSys 5 Scientific Modeling Package. Groundwater. 2020. 59: 117–122. doi.org/10.1111/gwat.13017.