Описание камнепадов и инженерная защита от них: обзор. Часть 3

МОДЕЛИРОВАНИЕ ТРАЕКТОРИЙ КАМНЕПАДОВ

Важно описать движение падающего камня вниз по склону, то есть его траекторию. Это позволяет описать подверженность камнепадам участков на этом склоне или под ним или оценить опасность для них. Кроме того, информация о скорости движения камней, высоте их отскоков и пространственном распределении их траекторий является основой для правильного проектирования и проверки эффективности защитных мер.

Траектории камнепадов могут быть приблизительно описаны аналитическими методами. Если же необходим более подробный анализ и надо учитывать вероятностную информацию, рекомендуется использовать численные методы.

Поэтому в данной части делается попытка кратко рассказать о доступных в настоящее время моделях траекторий камнепадов. Для этого существующие многочисленные модели можно разделить на группы, во-первых, на основе размерности их пространства: двумерные (2D); квазитрехмерные (2,5D) и трехмерные (3D). Во-вторых, модели траекторий камнепадов можно классифицировать в соответствии с лежащими в их основе расчетными принципами.

Размерность пространства модели является необходимым предварительным условием для получения приемлемых результатов (с ошибкой 20% по Berger, Dorren, 2006) независимо от лежащей в основе этой модели процедуры расчетов, опыта ее применения, информации о ее чувствительности к заданию параметров, а также от того, как определять значения ее параметров в полевых условиях.

Типы моделей камнепадов

Двумерные модели траекторий камнепадов

Двумерные модели имитируют траектории камнепадов в пространственной области, определяемой двумя осями. К первому их типу относятся модели, в которых расчеты производятся вдоль определенного пользователем профиля склона (Azzoni et al., 1995), который определяется осью расстояний (x или y) и осью высоты (z). Такой профиль часто идет вдоль линии наиболее крутого спуска. Из таблицы 1 видно, что к этой группе относится большинство моделей траекторий камнепадов.

Таблица 1. Основные характеристики ряда существующих моделей траекторий камнепадов (по Guzzetti et al., 2002)

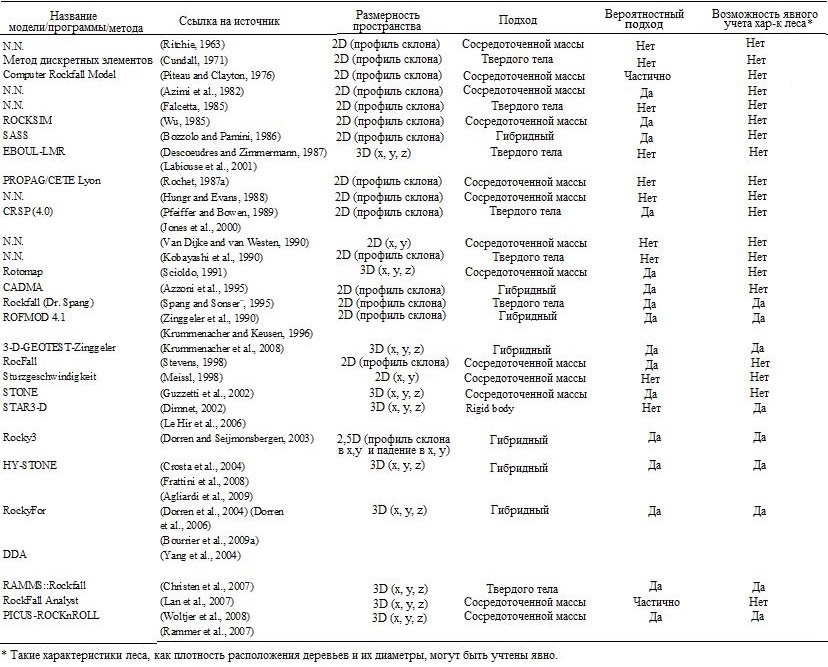
Во втором типе 2D-моделей траектории камнепадов рассчитываются в пространственной области, определяемой двумя осями расстояний (x и y), например на растровом изображении (на сетке) со значениями высот или на карте с изолиниями. В таких моделях обычно рассчитываются траектории камнепадов на основе топографо-гидрологических подходов, а также скорости и дальности выброса с использованием подхода скольжения камней (Van Dijke, VanWesten, 1990; Meissl, 1998). Но они не дают информации о высоте отскока.

Квазитрехмерные модели траекторий камнепадов

Вторая рассматриваемая группа – это квазитрехмерные (2,5D) модели траекторий камнепадов. Это просто 2D-модели, в которых при получении заранее определенных траекторий падения помогают геоинформационные системы (ГИС). Ключевой особенностью таких моделей является то, что направление траектории камнепада в области x, y не зависит от кинематики падающих камней и их траекторий в вертикальной плоскости. В этих моделях расчет горизонтального направления падения (в области x, y) может быть полностью отделен от расчетов кинематики камнепада, мест и высот отскоков. Это означает, что в них фактически выполняется два отдельных 2D-вычисления. С помощью первого определяется положение профиля склона в области x, y, а второе представляет собой двумерное моделирование камнепада вдоль ранее определенного профиля склона.

Примерами являются те модели, в которых рассчитывается кинематика камнепада вдоль профиля склона, соответствующего самому крутому спуску, определенному с использованием цифровых данных о местности, например в модели Rocky3 (Dorren, Seijmonsbergen, 2003).

Трехмерные модели траекторий камнепадов

Третья рассматриваемая группа – это модели, в которых вычисляются траектории камнепадов в трехмерном пространстве (x, y, z) на каждом этапе расчета. В них имеется  взаимозависимость между направлением траектории камнепада в области x, y, кинематикой падающего камня, местами и высотами отскоков и, если это включено, воздействием на деревья. Приведем примеры таких моделей (см. также Masuya et al., 1999):

• EBOUL-LMR (Descoeudres, Zimmermann, 1987);
• STONE (Guzzetti et al., 2002);
• Rotomap (Scioldo, 2006);
• DDA (Yang  et al., 2004);
• STAR3-D (Dimnet, 2002);
• HY-STONE (Crosta et al., 2004);
• Rockyfor3-D (Dorren et al., 2004);
• RAMMS:Rockfall (Christen et al., 2007);
• Rockfall-Analyst (Lan et al., 2007);
• PICUS-ROCKnROLL (Rammer et al., 2007; Woltjer et al., 2008).

Основное преимущество 3D-моделей заключается в том, что на результирующих картах четко отражаются воздействия рельефа на расхождение и схождение траекторий, а также исключительные или неожиданные траектории, то есть те, которые на первый взгляд менее ожидаемы в полевых условиях.

Недостатком трехмерных моделей является необходимость в картах с пространственно явными параметрами, получение которых требует гораздо больше временных затрат на полевые исследования, чем определение значений параметров для моделирования траекторий на основе профиля склона.

Подходы к расчетам

Вторая главная особенность, которая позволяет различать типы моделей траекторий камнепадов и которая тесно связана с расчетами отскоков, – это представление в них камней. Тут можно выделить три подхода.

1. Как показано в таблице 1, камень можно представить как сосредоточенную массу, то есть в виде одной безразмерной точки.

2. Либо его можно представить в виде твердого тела реальной геометрической формы (часто в виде сферы, куба, цилиндра или эллипсоида). Как правило, этот подход используется в детерминистских моделях.

3. При гибридном подходе для моделирования свободного падения камень представляют как сосредоточенную массу, а для моделирования его качения, удара и отскока его рассматривают как твердое тело определенной формы (Crosta et al., 2004; Frattini et al., 2008; Agliardi et al., 2009).

Для расчетов отскоков камней от поверхности склона и коэффициентов трения при их качении большинство моделей траекторий камнепадов используют нормальный и тангенциальный коэффициенты реституции, или восстановления при ударе (коэффициент реституции COR соответствует отношению конечной энергии к начальной после столкновения двух объектов. – Ред.) (подробнее – см. Guzzetti et al., 2002; Scioldo, 2006). В таких моделях для выбора значений параметров, используемых для расчетов фактических отскоков, обычно применяется вероятностный подход (см. таблицу 1). Это необходимо для учета большой изменчивости реальных значений этих параметров из-за рельефа местности, формы камней и их кинематики во время отскоков.

Одна из предложенных моделей отскока (Bourrier et al., 2009b) связала угол удара, поступательную скорость и скорость вращения до и после отскока на основе многомерных случайных (стохастических) функций, что дало многообещающие результаты для скалистых склонов. Существуют также модели, которые для расчетов отскоков используют вышеупомянутые детерминистские подходы. В этих моделях в основном используется метод дискретных элементов (Cundall, 1971) и, например, такие его разновидности, как дискретный деформационный анализ (Yang et al., 2004) и теория ударных воздействий (Dimnet, 2002).

Параболические свободные падения рассчитываются с помощью стандартных алгоритмов для равномерно ускоренного параболического движения, за исключением тех моделей, которые используют подход скольжения камней для расчетов скорости камнепада по всей его траектории.

Взаимодействие камней со склоном

Траектории падающих камней можно описать как результаты комбинаций четырех типов движения: свободного падения, качения, скольжения и отскоков (Ritchie, 1963; Lied, 1977; Descoeudres, 1997). Встречаемость каждого из этих типов сильно зависит от угла наклона поверхности грунта (Ritchie, 1963). На крутых склонах чаще всего наблюдается свободное падение, тогда как на средних по крутизне поверхностях движение камней представляет собой последовательность свободных падений и отскоков. На пологих склонах преобладающими видами движения являются качение или скольжение.

Для выполнения анализа траекторий камней существует довольно много моделирующих камнепады программ. Задача заключается не в моделировании свободного полета, а в моделировании взаимодействий между падающим камнем и поверхностью склона. Соответствующие модели обычно подразделяют на две основные категории – основанные на методе твердого тела и основанные на методе сосредоточенной массы (Giani, 1992; Hungr, Evans, 1988). В первом методе и его вариантах падающий камень рассматривается как твердое тело, имеющее свои собственные форму и объем, решаются фундаментальные уравнения динамики и учитываются все типы движения, включая вращение (Azzoni et al., 1995; Cundall, 1971; Descoeudres, Zimmermann, 1987; Falcetta, 1985). Во втором методе и его вариантах принимается, что камень либо не имеет массы, либо его масса сосредоточена в одной точке, и при этом не учитываются ни его форма, ни его вращательное движение (Guzzetti et al., 2002; Hoek, 1987; Hungr, Evans, 1988; Piteau, Clayton, 1977; Ritchie, 1963; Stevens, 1998).

Существуют и другие программы, которые можно рассматривать как гибридные. Они используют преимущества быстрого и легкого моделирования свободного полета для сосредоточенной массы, но учитывают геометрические и механические характеристики камня и склона для моделирования удара (Azimi, Desvarreux, 1977; Bozzolo, Pamini, 1986; Dorren et al., 2004; Jones et al., 2000; Kobayashi et al., 1990; Pfeiffer, Bowen, 1989; Rochet, 1987b; Crosta et al., 2004).

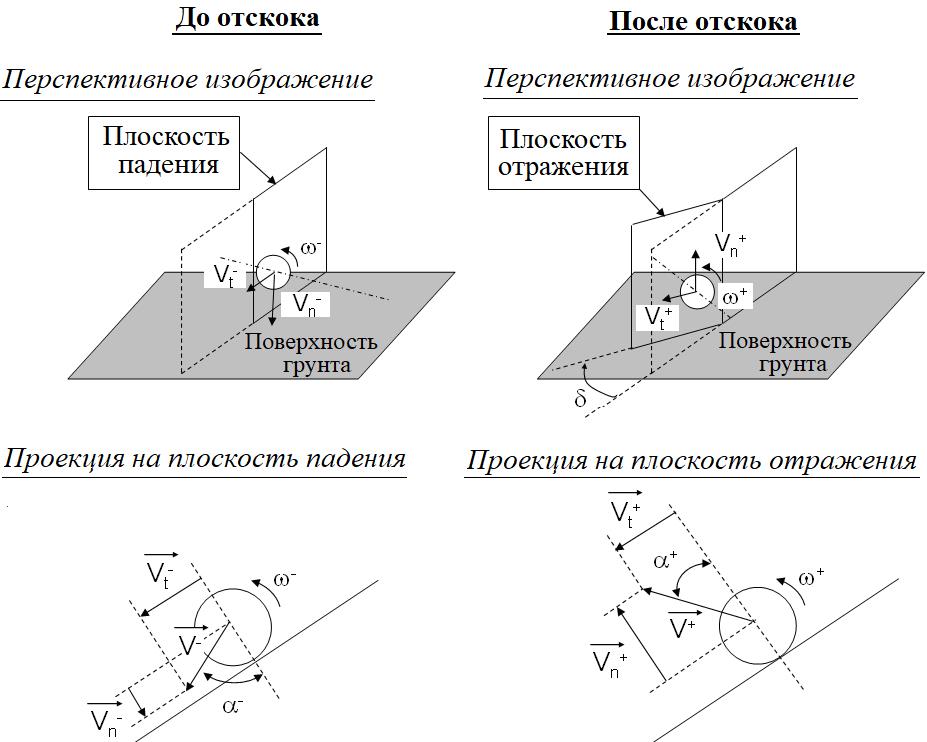
Если трехмерное моделирование камнепада основано на «псевдодвумерном» подходе (то есть выполняется квазитрехмерное моделирование – 2,5D), то тангенциальная (V_t^-) и нормальная (V_n^-) компоненты скорости камня относительно поверхности склона до удара позволяют определить плоскость, называемую плоскостью падения (рис. 6). Аналогично тангенциальная (V_t⁺) и нормальная (V_n⁺) составляющие скорости после отскока позволяют определить плоскость, называемую плоскостью отражения. Угол δ между этими двумя плоскостями называется углом отклонения. Нормальная (V_n⁺), тангенциальная (V_t⁺) и угловая (вращения, ω⁺) скорости после отскока вычисляются по нормальной (V_n^-), тангенциальной (V_t^-) и угловой (ω^-) скоростям до удара с использованием модели отскока, и определяется угол отклонения δ, что приводит к полному определению скорости камня после отскока.

Рис. 6. Определение скорости камня до и после отскока

Модели скольжения и качения

Скольжение в основном происходит на малых скоростях, когда камень только начинает двигаться или останавливается. Это не учитывается во многих моделях камнепадов, потому что не влечет за собой больших перемещений.

Качение в чистом виде происходит довольно редко, за исключением случаев на настолько слабых грунтах, что камни немного погружаются в них (Bozzolo, Pamini, 1986; Ritchie, 1963). Провести различие между режимами скольжения и качения иногда трудно, поскольку эти два типа движений могут комбинироваться (Descoeudres, 1997; Giani, 1992). На более жестких обнаженных грунтах из-за неровной поверхности склона и формы падающего камня «качение» скорее представляет собой последовательность небольших отскоков.

Поэтому в большинстве моделей камнепадов траектории камней моделируются как последовательности свободных падений и отскоков. Скольжение и качение рассматривают и учитывают лишь немногие авторы (например, Azzoni et al., 1995; Bozzolo, Pamini, 1986; Statham, 1979), и в их моделях вводится тангенциальный коэффициент демпфирования, связанный с трением качения и/или скольжения между камнем и склоном. Трение скольжения определяется с помощью нормальной составляющей веса камня по отношению к поверхности грунта в соответствии с законом Кулона. Для качения было дано довольно точное описание также с помощью закона Кулона с коэффициентом трения качения, который зависит от характеристик камня (его размера и формы) и склона (типа и размера элементов обломочного материала на его поверхности) (Statham, 1979).

Условие перехода между режимами отскоков и качения обсуждается в ряде публикаций, приведенных в списке литературы (Piteau, Clayton, 1977; Hungr, Evans, 1988; Giani, 1992). Переход от скольжения к качению хорошо определен в одной известной авторам работе (Bozzolo et al., 1988).

Вся траектория падающего со склона камня иногда моделируется как скольжение или качение тела некой массы по наклонной поверхности грунта со средним углом внутреннего трения, который считается репрезентативным для средних потерь энергии вдоль всего пути (Evans, Hungr, 1993; Govi, 1977; Hungr, Evans, 1988; Japan Road Association, 1983; Lied, 1977; Rapp, 1960; Toppe, 1987b). Этот метод (называемый методом угла тени, или методом конуса) обеспечивает быстрое и недорогое предварительное определение территорий, находящихся под угрозой камнепадов, как в локальном, так и в региональном масштабе (Jaboyedoff, Labiouse, 2003; Meissl, 2001).

Модели отскоков

Отскок происходит, когда падающий камень сталкивается с поверхностью склона. Высота и направление отскока зависят от нескольких параметров, характеризующих условия удара. Из четырех типов движения, которые происходят во время камнепада, тип отскоков является наименее изученным и наиболее трудным для прогнозирования.

Ряд моделей камнепадов представляет отскок в упрощенном виде с помощью одного или двух общих коэффициентов, уже упомянутых выше, которые называются коэффициентами реституции. Некоторые модели используют только один коэффициент реституции, количественно оценивая диссипацию энергии через потерю величины скорости (Kamijo et al., 2000; Paronuzzi, 1989; Spang, Rautenstrauch, 1988; Spang, Sonser, 1995) или через потерю кинетической энергии (например, Azzoni et al., 1995; Bozzolo, Pamini, 1986; Chau et al., 1999a; Urciuoli, 1988). В этом случае для полного определения вектора скорости после удара необходимо принять допущение относительно направления отскока, то есть угла α⁺ (см. рис. 6). Коэффициент R_V учитывают при составлении формулы с точки зрения потери скорости, а коэффициент R_E используют при составлении формулы с точки зрения кинетической энергии (в целом пренебрегая вращательной частью движений):

Однако наиболее распространенное определение отскока камня включает различение тангенциального (R_t) и нормального (R_n) коэффициентов реституции (Budetta, Santo, 1994; Evans, Hungr, 1993; Fornaro et al., 1990; Giani, 1992; Guzzetti et al., 2002; Hoek, 1987; Kobayashi et al., 1990; Pfeiffer, Bowen, 1989; Piteau, Clayton, 1976; Urciuoli, 1988; Ushiro et al., 2000; Wu, 1985):

Эти коэффициенты используются совместно и характеризуют уменьшение тангенциальной и нормальной составляющих скорости камня соответственно. Это позволяет полностью определить направление отскока, то есть угол α⁺ (см. рис. 6), и при этом не требуется никаких дополнительных допущений.

Альтернативный подход основан на теории удара (Fremond, 1995; Goldsmith, 1960; Stronge, 2000). В нем учитывается изменение момента количества движения камня во время фаз сжатия и восстановления (реституции) при ударе (Bozzolo et al., 1988; Descoeudres, Zimmermann, 1987; Dimnet, 2002; Dimnet, Fremond, 2000).

Согласно теории удара Ньютона коэффициенты реституции должны иметь постоянные значения независимо от энергии удара («упругого» столкновения) и его направления. Однако, поскольку это допущение не соответствует результатам наблюдений, было разработано несколько моделей для учета зависимости скорости камня после отскока от кинематических условий до удара (Bourrier et al., 2009b; Chau et al., 2002; Dorren et al., 2004; Heidenreich, 2004; Pfeiffer, Bowen, 1989). Эти модели можно рассматривать как результаты усовершенствования классических моделей, основанных на постоянных коэффициентах реституции.

Кроме того, были разработаны некоторые очень детальные модели взаимодействия между камнем и склоном (Azimi et al., 1982; Falcetta, 1985; Ushiro et al., 2000). В них различаются удары о поверхность твердых и слабых грунтов, учитывая для последних небольшое погружение камня в грунт, моделируемое как идеально-пластическое или идеально-упругопластическое поведение. Что касается фрагментации камней, которая может произойти при ударе о твердый грунт, то она редко учитывается (Azimi et al., 1982; Chau et al., 1998a; Fornaro et al., 1990), поскольку разработчики моделей обычно принимают, что неразрушаемые камни распространяются дальше, чем разрушаемые.

И наконец, помимо моделей твердого тела, в которых используются сочетания фундаментальных уравнений движения, только некоторые модели учитывают скорость вращения вдоль траектории камня. В этом случае обычно устанавливается взаимосвязь между поступательным движением и вращением при допущении, что камни отрываются от земли после удара в режиме качения. На поверхности контакта рассматриваются и учитываются условия либо «прилипания» («застревания» – sticking), либо скольжения (Chau et al., 2002; Kawahara, Muro, 1999; Ushiro et al., 2000).

Барьерный эффект деревьев

Существует лишь несколько моделей пространственных траекторий камнепадов, которые явно учитывают защитный эффект существующего лесного покрова (например, через пространственное распределение древостоев, плотность стояния деревьев, распределение их диаметров на уровне груди, их виды) (Dorren et al., 2006; Crosta et al., 2004; Krummenacher et al., 2008; Woltjer et al., 2008; Masuya et al., 2009 и др.). Эти модели могут помочь в определении оптимальных сочетаний и мест проведения технических и лесохозяйственных мероприятий на интересующем участке. Кроме того, они позволяют зонировать опасность камнепадов с учетом защитного действия лесов и без него.

В некоторых работах, опубликованных незадолго до настоящей статьи, неплохо описан эффект рассеивания энергии камней деревьями (Dorren, Berger, 2006; Jonsson, 2007 и др.). Но более старые данные серьезно занижали способность деревьев рассеивать энергию, то есть ранее считалось, что зрелые хвойные деревья рассеивают до 15 кДж вместо 200–500 кДж (Dorren et al., 2007).

Моделирование изменчивости

Детерминистский прогноз взаимодействия между камнем и поверхностью склона неуместен, потому что наше понимание таких явлений не является достаточным и многие параметры не охарактеризованы полностью. Неопределенности связаны с падающим камнем (его формой, размерами), топографией (наклоном, неровностями поверхности) и грунтами, слагающими обнажения (их прочностью и жесткостью). Как следствие, даже при тщательном полевом исследовании сбор данных не может быть исчерпывающим, поэтому прогноз отскока должен учитывать определенную изменчивость.

Из-за этого были предложены вероятностные модели отскоков (Agliardi, Crosta, 2003; Azzoni et al., 1995; Bourrier et al., 2009b; Dudt, Heidenreich, 2001; Guzzetti et al., 2002; Paronuzzi, 1989; Pfeiffer, Bowen, 1989; Wu, 1985).

Модель, правильно оценивающая изменчивость отскоков, должна разделять разные источники неопределенности (обусловленные случайностью характеристик или отсутствием данных) и количественно определять изменчивость, связанную с каждым из них по отдельности.

Изменчивость отскоков количественно оценивается несколькими статистическими законами, которые необходимо калибровать на основе статистического анализа результатов ударов.

Обратный анализ наблюдаемых событий или полевых экспериментов для этой цели невозможен, поскольку либо набор данных является неполным, либо воспроизводимые условия удара трудно достижимы. С другой стороны, можно использовать обширные лабораторные эксперименты или тщательно откалиброванное численное моделирование. Эти подходы уже использовались для крупнозернистых грунтов (Bourrier et al., 2009b). Задача такого подхода заключается в создании требуемых наборов данных, состоящих из результатов, полученных для разных свойств грунта и кинематических условий до отскока.

Важность параметров удара

Как показал анализ ряда различных определений коэффициентов реституции, используемых в компьютерных программах, отскок камня от поверхности склона все еще остается малоизученным явлением. В частности, моделирование с помощью постоянных коэффициентов реституции только в зависимости от грунта на поверхности склона не очень приемлемо, по крайней мере с научной точки зрения. Действительно, как упоминалось выше, отскок зависит также от нескольких параметров, связанных с камнем и его кинематикой до удара (таблица 2). Поэтому целесообразно выполнение экспериментальных исследований влияния этих параметров для достижения более глубокого понимания механизмов ударов, для получения математических выражений, связывающих коэффициенты реституции и эти параметры, а также для возможного определения надежных значений параметров, используемых в моделях отскоков.

Таблица 2. Принятые параметры, которые влияют на отскок камня от поверхности склона (Labiouse, Descoeudres, 1999)

Соответствующие экспериментальные исследования проводились как в полевых условиях (Azzoni, De Freitas, 1995; Azzoni et al., 1992; Berger, Dorren, 2006; Bozzolo et al., 1988; Broili, 1977; Evans, Hungr, 1993; Fornaro et al., 1990; Giacomini et al., 2009; Giani, 1992; Japanese highway public corporation, 1973; Kirkby, Statham, 1975; Kobayashi et al., 1990; Lied, 1977; Pfeiffer, Bowen, 1989; Ritchie, 1963; Statham, 1979; Statham, Francis, 1986; Teraoka et al., 2000; Urciuoli, 1996; Wu, 1985; Yoshida, 1998 и др.), так и в лаборатории (Azimi, Desvarreux, 1977; Azimi et al., 1982; Bourrier, 2008; Camponuovo, 1977; Chau et al., 1998a, 1999a, 2002, 1999b, 1998b; Heidenreich, 2004; Kamijo et al., 2000; Kawahara, Muro, 1999; Murata, Shibuya, 1997; Statham, 1979; Ujihira et al., 1993; Ushiro et al., 2000; Wong et al., 2000, 1999; Masuya et al., 2001). Эти эксперименты поспособствовали определению наиболее важных параметров удара камня о поверхность склона и количественной оценке их влияния на отскок.

Экспериментальные исследования показали зависимость отскока камня от геометрических параметров, в том числе от «шероховатости» склона (обычно характеризуемой отношением размера камня к среднему размеру элементов обломочного материала, покрывающего поверхность). Влиянием «шероховатости» склона на отскок обычно объясняют сортировку камней по размеру вниз по профилю (Kirkby, Statham, 1975; Statham, Francis, 1986). Действительно, когда размер падающего камня превышает средний размер частиц обломочного материала на поверхности склона, преобладающим типом его движения является качение – и он в итоге оказывается дальше (Bozzolo, Pamini, 1986; Evans, Hungr, 1993; Giani, 1992; Kirkby, Statham, 1975; Ritchie, 1963; Statham, Francis, 1986). Однако при слабых грунтах на склоне увеличение веса камня вызывает более сильную пластическую деформацию поверхности (образование большего «кратера»), а это несколько уменьшает дальность его продвижения. Что касается формы камней, то испытания, проведенные с использованием кубических блоков, показали, что конфигурация удара (например, гранью, ребром или углом) оказывает очень большое влияние на движение блока во время и после удара (Giani, 1992; Heidenreich, 2004).

Было обнаружено, что отскок существенно зависит от передачи энергии от падающего камня склону. Часть исходной (до столкновения) кинетической энергии камня уходит с ударной волной от точки его контакта со склоном (Bourrier et al., 2008; Giani, 1992). Происходит также диссипация энергии, которая связана с процессами трения и пластических деформаций в материале склона во время удара (Bourrier et al., 2008; Bozzolo, Pamini, 1986; Giani, 1992; Heidenreich, 2004), а также с фрагментацией камня и/или частиц грунта (Azimi et al., 1982; Fornaro et al., 1990; Giani, 1992). Величина диссипации энергии в основном определяется соотношением между размерами камня и частиц грунта на склоне (Bourrier et al., 2008; Statham, 1979), свойствами грунта (Azzoni et al., 1995, 1992), а также формой камня и ориентацией его падения (Chau et al., 1999a; Falcetta, 1985; Heidenreich, 2004). Упругая деформация материала поверхности склона также имеет место, но в общем случае ею можно пренебречь.

Указанные процессы потери энергии также сильно зависят от кинетической энергии камня до удара, которая связана с его массой m и скоростью (V^-) перед столкновением, то есть E_c=1/2*m*(V^-)². Влияние массы (Jones et al., 2000; Pfeiffer, Bowen, 1989; Ushiro et al., 2000) и скорости (Urciuoli, 1988; Ushiro et al., 2000) камня перед ударом различно из-за линейных и квадратичных зависимостей.

Еще одной очень важной особенностью, наблюдавшейся во многих экспериментах, является сильное влияние кинематических условий до отскока. В частности, эксперименты показали, что небольшие углы падения приводят к большему сбережению энергии камня (Bozzolo, Pamini, 1986; Chau et al., 2002; Heidenreich, 2004; Ushiro et al., 2000; Wu, 1985). Действительно, только небольшая часть кинетической энергии камня до удара связана с составляющей скорости, перпендикулярной поверхности грунта, и, следовательно, диссипация этой компоненты энергии в грунте меньше. С другой стороны, значительная часть кинетической энергии, относящейся к тангенциальной составляющей скорости, сохраняется камнем после удара, причем часть ее (до 30%) преобразуется в энергию вращения (Kawahara, Muro, 1999; Ushiro et al., 2000). Скорость вращения после отскока в значительной степени зависит от угла падения до удара и от типа грунта. Это определяется условиями взаимодействия на поверхности контакта, такими как «прилипание» («застревание» – sticking) или скольжение (Chau et al., 2002).

Большинство вышеупомянутых экспериментальных исследований оказалось недостаточным для полного понимания рассматриваемого явления или для его статистического и параметрического анализа. Поэтому также проводились систематические лабораторные эксперименты на моделях малого и среднего масштаба (Bourrier, 2008; Chau et al., 2002; Heidenreich, 2004). Их целью был анализ влияния на отскок параметров, связанных с грунтом, падающим камнем и его кинематикой. Имитирующие камни тела (в основном сферические) бросались на разные грунтовые материалы с разной степенью уплотнения либо в перпендикулярном направлении, либо под разными углами с использованием специальных метательных устройств. Ход всех опытов снимался с помощью высокоскоростных видеокамер.

Отметим, что в отличие от полевых экспериментов контролируемые лабораторные опыты дают точно измеренные и воспроизводимые результаты, которые действительны и в более широких областях. Поэтому выявленные с их помощью тенденции могут быть с уверенностью использованы для усовершенствования моделей отскока. Кроме того, результаты лабораторных экспериментов дают много информации, важной для калибровки численных моделей удара, которые, в свою очередь, могут быть использованы для изучения передачи энергии во время удара (Bourrier et al., 2008). Однако количественная интерпретация результатов лабораторных опытов не является простой, поскольку бывает трудно обеспечить соответствие требованиям подобия для всех параметров, участвующих в динамическом процессе (Bourrier, 2008; Camponuovo, 1977; Heidenreich, 2004).

Основные результаты этих экспериментов подтвердили общие тенденции, выявленные при предыдущих исследованиях. Относительно влияния характеристик грунта на поверхности склона было обнаружено, что на движение камня во время и после удара существенно влияет степень уплотнения этого грунта и в несколько меньшей степени – угол его внутреннего трения (Bourrier, 2008; Heidenreich, 2004). Что касается влияния кинематики камня до удара, то опыты подтвердили четкую зависимость коэффициентов реституции от его скорости и угла удара о поверхность. Влияние последнего, по-видимому, преобладает (Bourrier, 2008; Chau et al., 2002; Heidenreich, 2004). Кроме того, зависимость от массы и размера камня более заметна при перпендикулярном ударе, чем при меньших углах падения, потому что в первом случае передача энергии грунту больше (Bourrier, 2008; Heidenreich, 2004). Также было показано, что форма камня и его конфигурация при столкновении явно влияют на его движение после удара, особенно на скорость вращения. И наконец, большое количество экспериментальных результатов позволило (в частности, для крупнозернистых грунтов) количественно оценить большую изменчивость кинематики камня после отскока в зависимости и от формы поверхности, и от геометрической конфигурации частиц грунта в зоне удара (Bourrier et al., 2009б, 2008).

Результаты вышеупомянутых лабораторных опытов позволили определить наиболее важные геометрические и геотехнические параметры, влияющие на отскок, и получить формулы для коэффициентов реституции в зависимости от характеристик удара (Bourrier, 2008; Chau et al., 2002; Heidenreich, 2004). С практической точки зрения использование этих математических зависимостей в компьютерных программах должно привести к более хорошему прогнозированию отскока. Это может улучшить определение зон риска, особенно для участков, где еще не было камнепадов и/или не проводилось наблюдение за ними.

Однако с научной точки зрения пригодность коэффициентов реституции, выраженных для центров масс камней (см. формулы (3) и (4)), подвергается сомнению (Labiouse, Heidenreich, 2009). Действительно, при тщательном анализе видеозаписей, сделанных скоростными камерами, было обнаружено, что движение камня во время удара состоит из трех основных взаимозависимых составляющих – перпендикулярного перемещения (внедрения в грунт), тангенциального перемещения (скольжения) и вращения. Было бы обманчиво моделировать этот сложных механизм с помощью двух общих коэффициентов реституции, полученных для центра масс камня, как это принято в большинстве существующих программ для моделирования траекторий камнепадов. Смоделировать явление удара можно только с помощью методов твердого тела, которые принимают во внимание форму камня и полностью учитывают взаимодействие между ним и грунтом на поверхности контакта (включая образование «кратера»).

Заключительные замечания по взаимодействию камня и склона

Количество различных моделей отскока, используемых при моделировании камнепадов, подчеркивает, что взаимодействие камней и склонов изучено все еще плохо. Это сложное явление зависит не только от грунтовых условий (жесткости, прочности, «шероховатости», наклона поверхности склона), но и от характеристик камня (его веса, размера, формы, прочности), а также от его кинематики перед ударом (скорости, угла столкновения, конфигурации при ударе). Поэтому следует иметь в виду, что при использовании обычных моделей отскока способность той или иной модели камнепада давать реалистичные прогнозы обусловлена хорошей калибровкой ее параметров на основе наблюдений и измерений в процессе естественных или искусственных камнепадов на интересующем участке. В случаях, когда для конкретной территории такие данные отсутствуют, следует иметь в виду, что расчеты траекторий камней могут быть весьма ошибочными, если они выполняются с коэффициентами реституции, взятыми из публикаций либо оцененными на основе камнепадов или их обратного анализа на других склонах.

Для повышения надежности моделирования траекторий было проведено (или все еще проводится) несколько исследований по разработке моделей отскока, учитывающих влияние наиболее важных параметров удара. Затем эти параметры могут быть откалиброваны с помощью более объективно собранных полевых данных. Для этого, а также чтобы достичь более глубокого понимания механизмов, задействованных при ударе, и количественно оценить влияние наиболее важных геометрических и геотехнических параметров, было выполнено множество экспериментов как в полевых, так и в лабораторных условиях.

После тщательной калибровки с использованием экспериментальных данных численное моделирование может поспособствовать изучению передачи энергии во время удара и оценке влияния параметров за пределами диапазона протестированных значений. На основе этих исследований могут быть получены формулы для параметров моделей отскока в зависимости от характеристик удара.

Использование моделей отскока в программах для моделирования камнепадов должно обеспечить более точные прогнозы траекторий и энергий этих событий и, следовательно, улучшить выявление (оконтуривание) зон риска и проектирование защитных сооружений.

Калибровка модели отскока

Как правило, параметры отскока, используемые для расчета траектории камня, оцениваются на основе приблизительного описания грунта на склоне (скального, каменистого осыпного, рыхлого), иногда дополняемого информацией о его «шероховатости», степени уплотнения и о его растительном покрове. Но, как было отмечено несколькими авторами, которые наблюдали за естественными и/или искусственными камнепадами in situ (Azimi et al., 1982; Azzoni, De Freitas, 1995; Falcetta, 1985; Giani, 1992; Hungr, Evans, 1988 и др.), характеристики движения после удара обусловлены несколькими факторами, не относящимися к свойствам материала склона, а именно весом, размером и формой камня, а также его скоростью, углом столкновения и конфигурацией при ударе. Следовательно, коэффициенты реституции, характеризующие отскоки камней во время камнепадов, зависят не только от грунта на поверхности склона.

Поскольку наши знания о явлении отскока и о его моделировании являются неполными, а описания грунтов, слагающих склоны с поверхности, довольно субъективны, надежность результатов моделирования можно было бы улучшить. Это становится очевидным при сравнении результатов, полученных для конкретного участка с помощью различных моделей или даже с использованием одной и той же программы, но разными пользователями (Berger, Dorren, 2006; Labiouse, 2004; Labiouse et al., 2001). Ограничения прогнозов также очевидны, когда значения параметров модели, взятые из литературы или полученные в результате испытаний in situ или обратного анализа природных явлений для конкретных склонов, не дают удовлетворительных результатов при использовании для других склонов.

Для достижения высокой надежности прогнозирования траекторий камнепадов параметры программы должны быть тщательно откалиброваны на интересующем участке. С этой целью во время сбора полевых данных особое внимание следует уделять получению информации о траекториях предыдущих камнепадов по таким признакам, как «шрамы» на скалах, следы воздействий на склоны, повреждения растительности и зоны аккумуляции. При условии, что численная модель хорошо откалибрована с учетом результатов таких полевых наблюдений, уверенность в правильности моделирования траекторий будет значительно выше.

Сбор и анализ полевых данных

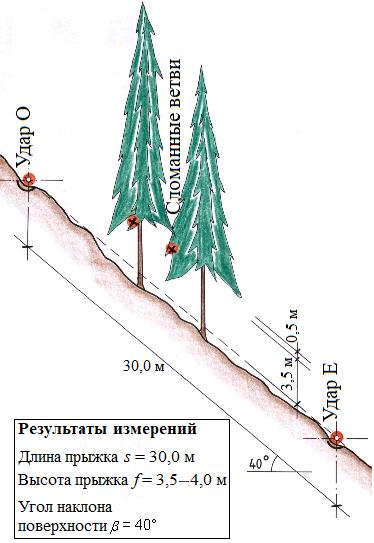
Для полного обратного анализа траектории камня должны быть известны высотные отметки начала его движения и остановки. Кроме того, необходимо нанести на карту горизонтальную проекцию траектории, чтобы получить длину этой проекции. Надо также выявить как можно больше следующих друг за другом ударных «кратеров», наклонные расстояния s между ними и угол наклона поверхности грунта. Также следует зарегистрировать линии движения камня над землей, позволяющие определить высоту отскоков. Однако эти линии обычно относятся к центру тяжести камня, тогда как пути его движения по поверхности грунта относятся к его нижнему краю. Это следует учитывать в случаях небольших высот отскоков в сочетании с очень крупными камнями. В редких случаях можно измерить даже максимальную высоту прыжка f, измеренную по вертикали на расстоянии s/2 от места отскока, если наклон склона существенно не меняется (рис. 7). Однако в большинстве случаев высота прыжка f должна оцениваться в зависимости от длины прыжка s вдоль наклонной поверхности. Наблюдения показывают, что для характерных скачков справедливы следующие соотношения:

f/s = 1/6 для высоких отскоков;

f/s = 1/8 для обычных средних отскоков;

f/s = 1/12 для мелких отскоков.

Рис. 7. Схематическое изображение пути движения камня и его проекция на наклонную плоскость

Если следы на земле не могут быть отнесены к отдельным прыжкам из-за нескольких перекрывающихся траекторий камней, то следует зарегистрировать профиль склона вдоль потенциальной траектории. Это может позволить смоделировать перемещения камня позднее.

По полевым данным можно определить «воздушные параболы» одиночных прыжков с соответствующими скоростями. На рисунке 7 верхний ударный «кратер» O соответствует началу такой параболы, а другому ее концу соответствует нижний «кратер» E. Начальную скорость отскока (отрыва от земли) обозначим v_O, а ее горизонтальную и вертикальную составляющие – соответственно v_Оx и v_Оz. Скорость следующего удара обозначим v_E, а ее горизонтальную и вертикальную составляющие – соответственно v_Ex и v_Ez.

Высота прыжка f определяется в середине его наклонной длины s (рис. 8). Горизонтальная (x) и вертикальная (z) проекции длины прыжка s при угле наклона поверхности грунта β находятся по формулам:

Рис. 8. «Воздушная парабола», описываемая камнем при скачке, с векторами скоростей

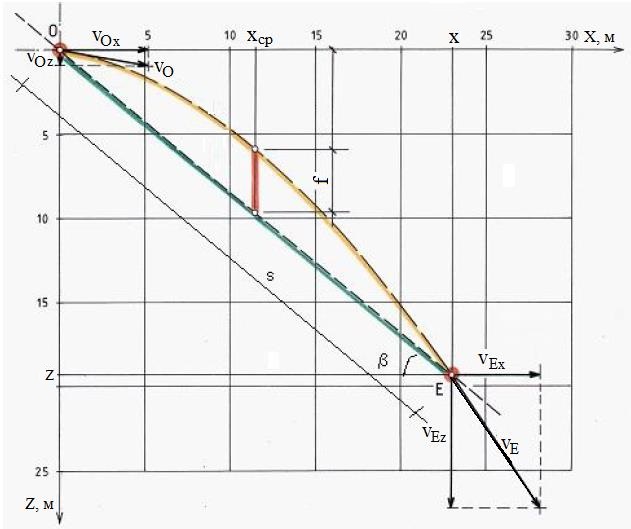
Горизонтальная и вертикальная составляющие скорости отрыва камня соответственно:

В результате получаем формулу для общей скорости отрыва:

Здесь g обозначает гравитационную постоянную, равную 9,81 м/с², а вертикальному направлению вверх соответствует положительный знак.

Соответственно, скорость удара:

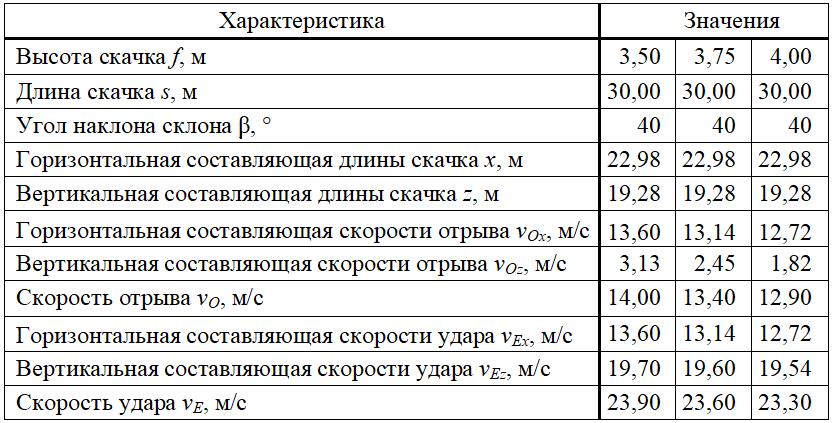
В качестве примера можно привести ряд измеренных значений (см. рис. 7), который приведет к скоростям, показанным в таблице 3. Различные принятые высоты прыжка от 3,5 до 4,0 м приведут к схожим скоростям отрыва и удара.

Таблица 3. Начальная и конечная скорости движения камня по параболической траектории для различных значений высоты скачка (см. рис. 7)

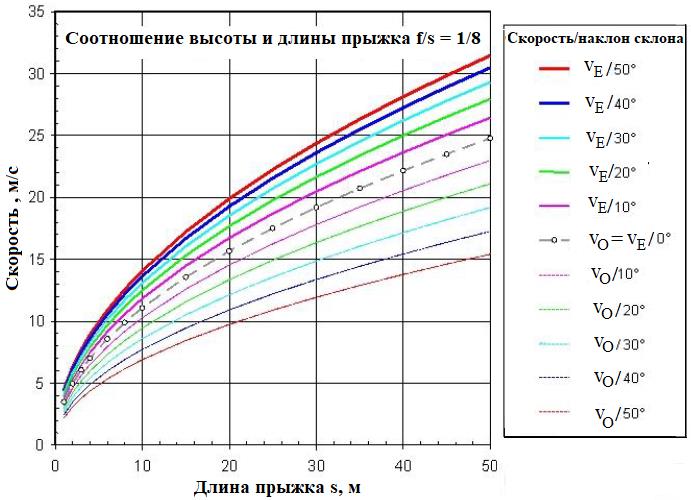
Определение начальной (v_O) и конечной (v_E) скоростей можно упростить и ускорить, используя диаграмму, которая зависит от длины скачка s и угла наклона поверхности грунта β, если принять соотношение высоты и длины прыжка f/s = 1/8 (рис. 9). Такие графики можно легко построить и для любого другого отношения f/s.

Рис. 9. Графики скоростей отрыва и удара при соотношении высоты и длины прыжка f/s = 1/8 в качестве инструмента для быстрого анализа траектории камня при камнепаде в полевых условиях

-

В следующей части статьи, которая будет опубликована через неделю, речь пойдет о мерах защиты от камнепадов.

Список литературы, использованной авторами переведенного обзора [1], можно посмотреть в конце оригинальной статьи по ссылке nhess.copernicus.org/articles/11/2617/2011/nhess-11-2617-2011.pdf.

Источник

1. Volkwein A., Schellenberg K., Labiouse V., Agliardi F., Berger F., Bourrier F., Dorren L. K. A., Gerber W., Jaboyedoff M. Rockfall characterisation and structural protection – a review // Natural Hazards and Earth System Sciences. European Geosciences Union, Copernicus Publications, 2011. Vol. 11. P. 2617–2651. URL: nhess.copernicus.org/articles/11/2617/2011/.