Ранжирование итальянской железнодорожной сети по подверженности камнепадам и чувствительности к ним

ВВЕДЕНИЕ

Подверженность камнепадам участков вдоль транспортного коридора является постоянной темой в исследованиях оползневых процессов. Выводы, основанные на количественных исследованиях, актуальны для практических целей, поскольку они предоставляют ключевую информацию для снижения рисков и могут помочь в быстрой оценке возможных критических для транспортной сети мест, в планировании и проектировании защитных барьеров в таких местах.

Карта подверженности камнепадам не содержит информации ни о величине таких возможных событий, ни об их ожидаемой частоте. Стремление к такому полному описанию (то есть составление карты опасностей или рисков) потребовало бы знаний о процессах, ведущих к мобилизации отдельных блоков или массивов скальных пород в локальном масштабе.

К входным данным для составления карты подверженности камнепадам меньше требований, хотя собрать их для большой площади все же не так просто. Минимальными требованиями здесь являются: информация о местах начала камнепадов, о лежащей в основе этого топографии и наличие модели для описания транзита каменного материала. В большинстве исследований камнепадов, имеющихся к моменту публикации данной статьи, использовались физически обоснованные модели, поскольку они дают более точное описание всего процесса, но есть и немного примеров статистических моделей подверженности камнепадам (Frattini et al., 2008).

Существуют феноменологические (более простые) способы соотнесения источников камнепадов с местами их остановки, например с использованием эмпирического угла так называемого сектора тени (максимальной поражаемой зоны) с вершиной в точке начала камнепада (Evans, Hungr, 1993). Здесь авторами настоящей статьи [1] было решено использовать модель STONE, разработанную ранее Гуццетти и др. (Guzzetti et al., 2002). Для этой модели требуются: цифровая модель рельефа (ЦМР), заранее определенные места источников камнепадов и численные параметры, описывающие реституцию (восстановление) энергии при отскоках в местах ударов камней о поверхность склона. Авторы работы [1] использовали количество траекторий на ячейку сетки в модели для расчетов подверженности территорий камнепадам.

Для достижения поставленных целей авторы данного исследования [1] сделали следующее:

1) применили новый метод установления зон источников камнепадов для определения их траекторий (Alvioli et al., 2020b), основанный на экспертном картировании выборки зон источников и на статистическом обобщении по всей исследуемой территории;

2) выполнили вероятностное моделирование для подсчета траекторий с использованием модели STONE, которую в конечном итоге классифицировали как карту подверженности камнепадам национальной железнодорожной сети Италии;

3) выполнили анализ с помощью регулярных сеток в рамках теории графов, пытаясь определить влияние возможных событий на функциональность сети в целом.

Подтвердить эти результаты помогла национальная инвентаризация оползней, для которой использовалось и используется более 70 000 камнепадных полигонов.

ИСТОРИЯ ВОПРОСА

Физически обоснованное моделирование камнепадов

Камнепады имеют следующие стадии:

1) отрыв скального материала от поверхности склона (обычно крутого), как правило, путем скольжения, обрушения или падения;

2) последующее движение камней вниз по склону с различной динамикой.

Эти явления могут достаточно широко варьировать, причем двумя крайними случаями являются независимое падение отдельных скальных фрагментов без взаимодействия друг с другом и поток массы камней с взаимодействием или без взаимодействия с поверхностью склона (Bourrier et al., 2013). Явления, которые не подпадают строго под эти два предельных случая, содержат элементы обоих, и их труднее всего моделировать.

В данной работе [1] авторы не использовали физически обоснованную модель процесса отрыва. Насколько им было известно к моменту написания статьи [1], не существует модели, которая полностью бы охватывала весь многосторонний механизм инициирования камнепада (Collins, Stock, 2016; Matasci et al., 2018). Одной из возможностей избежать подробного описания этой стадии было бы прямое картирование по результатам наблюдений за скальными склонами, например с помощью лазерных сканеров (Jaboyedoff et al., 2012; Riquelme et al., 2014; Li et al., 2019), фотограмметрии (Buyer et al., 2020) и аналогичных подходов в сочетании с использованием беспилотных летательных аппаратов (Perez-Rey et al., 2019; Santangelo et al., 2019; Giordan et al., 2020). Такие измерения и алгоритмы могут предоставить подробную информацию о трещиноватости и/или нарушениях сплошности скальных грунтов, ориентации блоков и распределении трещин, что даст возможность сделать выводы о местоположении возможных зон отрыва каменного материала (Turanboy et al., 2018; Menegoni et al., 2021; Mavrouli, Corominas, 2020).

Описанные выше методы выявления потенциальных источников камнепадов применимы только на небольших площадях и, возможно, на отдельных склонах.

Еще один подход, который может быть очень эффективным и применяться к относительно большим территориям, представляет собой экспертное картирование возможных зон источников с помощью дешифрирования фотоснимков (аэрофотоснимков, космических снимков и др.) (Santangelo et al., 2019, 2020).

В своей работе [1] авторы стремились к оценке очень большой площади, поэтому ни один из этих методов не мог быть ими применен. Для достижения поставленных ими целей многообещающим мог бы быть такой метод многомерного статистического анализа, как регрессионный анализ (Rossi et al., 2021), но он не был использован, поскольку авторы исследования [1] выбрали метод, основанный на данных (Alvioli et al., 2020b), который будет описан позже.

Авторы статьи [1] имели дело только с отдельными падающими камнями, движущимися по независимым траекториям. Их можно описать с помощью баллистической динамики во время свободного падения, а также отскоков или качения по поверхности. В частности, в использованной авторами модели STONE принимается наличие «точечных» камней, перемещающихся только под действием силы тяжести и ограничений, обусловленных топографией и геологией. Компьютерная программа STONE трехмерно моделирует три возможных типа движения камня вдоль его траектории за ряд временных шагов до тех пор, пока движение не прекратится из-за исчерпания начальной кинетической энергии за счет трения.

Типы движения масс скальных фрагментов с траекториями, отличными от баллистических, то есть прерываемыми соударениями с поверхностью и отскоками или качением, не рассматривались в этой работе [1], поскольку для них требуются модели, подходящие для описания снежных и каменных лавин и каменных потоков, в то время как в модели STONE не учитываются взаимодействия между камнями и их фрагментация. Недавно Матас и др. (Matas et al., 2020) и Руис-Каррулла и др. (Ruiz-Carulla et al., 2020) подробно изучили механизм фрагментации больших скальных обломков и валунов, непосредственно наблюдая за их обломками после ударов о поверхность склона. Данные об угловом распределении этих обломков помогли откалибровать параметры модели RockGIS (Matas et al., 2017), реализующей фрактальную модель массы фрагментов, отсутствующую в STONE.

Чтобы выйти за рамки оценки пространственной подверженности, следует учитывать величину и периодичность возможных камнепадов (Guzzetti et al., 2003, 2004) на рассматриваемом участке. Их величина может варьировать в широком диапазоне объемов – от кубических дециметров до миллионов кубических метров (Hungr et al., 1999). Мельзнер и др. (Melzner et al., 2020) также исследовали частотно-размерные распределения, обнаружив зависимость от метода, используемого для картирования камнепадов, и, как и Короминас и др. (Corominas et al., 2018), рекомендовали проявлять осторожность при рассмотрении больших территорий. Авторы настоящей статьи [1] не рассматривали  величины камнепадов, так как модель STONE не учитывает их напрямую.

Авторы работы [1] также не учитывали конкретные триггеры. В действительности камнепады могут быть спровоцированы разными явлениями, чаще всего интенсивными дождевыми осадками и сейсмической активностью, но при этом на их возникновение влияют самые разные факторы (Macciotta et al., 2015). Статические факторы – это крутой склон и его строение, а динамические факторы – это термические деформации и/или циклы замерзания-оттаивания скальных грунтов. Существуют исследования корреляций между камнепадами и дождями, например с помощью вероятностных порогов атмосферных осадков (Melillo et al., 2020), и исследования связи между камнепадами и дождями, периодами заморозков и сильными колебаниями температуры (Delonca et al., 2014). Авторы работы [1] не включили в использованный ими метод описание, зависящее от триггера или времени, поскольку оно также выходит за рамки модели STONE.

Анализ железнодорожной сети в рамках теории графов

Теория графов – это математическое представление попарных взаимосвязей в совокупности объектов. Существует целая наука о графах с примерами в широком спектре теоретических и прикладных исследований (Chartrand et al., 1993). Одной из основных областей применения теории графов является представление физически существующей сети. Литература по науке о сетях и/или графах обширна и посвящена множеству явлений. Примерами физических сетей являются биологические и социальные сети, электросети, телекоммуникации, транспортные сети и даже «всемирная паутина» (Barthelemy, 2011). Исследования, связанные с транспортными сетями, часто охватывают городские условия, включая взаимозависимые и/или мультимодальные сети различных транспортных средств, а также коммуникационные сети (Alvioli, 2020).

В литературе также встречаются описания исследований эффектов от разрушения ряда вершин (узлов) или ребер. В работе Маттссона и Дженелиуса (Mattsson, Jenelius, 2015) имеется обзор устойчивости транспортных сетей. Несколько общих результатов, полученных ими, заключаются в том, что избыточность в сложной сети недостаточна для устойчивости к нарушениям и разрушениям, в то время как устойчивость намного выше для сетей, обладающих масштабной инвариантностью (Albert et al., 2000), как и для «всемирной паутины» (Cohen et al., 2000). С другой стороны, безмасштабные сети подвержены нарушениям при удалении нескольких соответствующих вершин. Особенностью сетей, важной для их устойчивости, является наличие петель (Katifori et al., 2010) и уязвимых мест (Bassolas et al., 2020).

В этой работе [1] используются основные понятия теории графов, полезные для понимания значимости конкретного ребра во всем графе. Сетью здесь называется набор физических связей (перегонов, или звеньев, железных дорог) и узлов (станций или пересечений путей), а графом – эквивалентное представление сети с помощью ребер и вершин. Элементы физической сети связаны с определенными географическими позициями, в то время как соответствующий ей граф представляет собой абстракцию, которая сохраняет только топологию физической сети и (необязательно) еще несколько величин.

Далее в работе [1] также говорится о центральности по промежуточности (степени посредничества) для вершин и ребер (Freeman, 1978, Lu, Zhang, 2013) - мере их значимости для функционирования всей соответствующей физической сети. Степень посредничества вершины/ребра определяется количеством кратчайших путей, проходящих через эту вершину/ребро, из общего множества кратчайших путей, соединяющих любые две пары вершин в графе (путей "все ко всем"). Центральность по промежуточности вершин/ребер зависит и от весов ребер в графе. Поскольку граф, рассматриваемый в статье [1], связан с физической сетью, вес ребер оценивается по фактической длине железнодорожных сегментов.

Авторы исследования [1] разработали новый (простой) показатель центральности по промежуточности, предназначенный для количественной оценки воздействия на сеть в результате удаления одного ребра, что имитирует прерывание функционирования соответствующего сегмента железной дороги из-за какого-либо внешнего события. Этот новый показатель позволяет проводить комбинированную классификацию участков железных дорог, основанную одновременно на их степени посредничества (значимости) и на подверженности камнепадам. В статье [1] авторы называют такую новую классификацию сети "ранжированной по подверженности и чувствительности к камнепадам". Схожий подход, а именно оценка рисков сети, сочетающая определение подверженности связующих сегментов отказам и их важности, был предложен Кэтсом и др. (Cats et al., 2016) для мультимодальной сети общественного транспорта в Нидерландах.

Доступные данные

В представленном исследовании [1] использовались как уже имеющиеся материалы, так и вновь построенные карты (последние включали общенациональную карту склоновых систем и карту выборок зон источников камнепадов). Перечислим и кратко опишем такие фрагменты информации.

1. Необходимая для всей последовательности обработки информации цифровая модель рельефа TINITALY с самым высоким разрешением, бесплатно доступная для всей Италии (Tarquini et al., 2007). Ячейки ее сетки соответствуют размерам 10 м x 10 м в системе координат EPSG:32633. На рисунке 1, а показана карта рельефа, основанная на модели EU-DEM  («Склоновые единицы на ЦМР») с разрешением 25 м (ее использование в данной работе [1] ограничено этой цифрой).

2. Материалы общенациональной инвентаризации камнепадов. Итальянская база данных по оползням (IFFI) (Trigila et al., 2010; ISPRA, 2018) содержит более 620 000 оползневых полигонов, из которых 70 576 относятся к камнепадным, а 4051 расположены в непосредственной близости от железнодорожных путей. Последние и использовались в данной работе [1] (камнепадными полигонами авторы статьи [1] называют территории, охватывающие зоны источников, движения и отложения камнепадов).

3. Мелкомасштабная (масштаба 1:100 000) литологическая карта Италии (Fongo, 2018; Bucci et al., 2021). На рисунке 1, б показана карта с 19-ю литологическими классами (расшифрованными в таблице 1).

4. Кадастровая карта Италии с отображением рельефа (Guzzetti, Reichenbach, 1994).

5. Общенациональная карта склоновых единиц (склоновых систем) (Alvioli et al., 2020a), в том числе опубликованная 21 августа 2018 года в отчете об исследовании P-05-1 (Unita territoriali di riferimento – «Территориальные единицы») проекта RFI-SERVICE Научно-исследовательского института гидрогеологической защиты Национального исследовательского совета Италии (IRPI-CNR). Карта содержит более 300 000 полигонов склоновых систем различных форм и размеров.

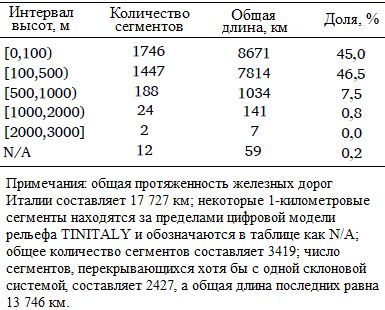
6. Векторная карта (векторный слой) железнодорожной сети. В таблице 2 показано распределение по высоте различных звеньев сети, а на рисунке 1, в отражены склоновые системы вдоль железнодорожных путей. На этом рисунке также показаны железнодорожные трассы на равнинных участках, где склоновые единицы не определены.

7. Карта выборки потенциальных источников камнепадов в пределах Италии на основе экспертной интерпретации снимков, взятых на сервисе Google Earth.

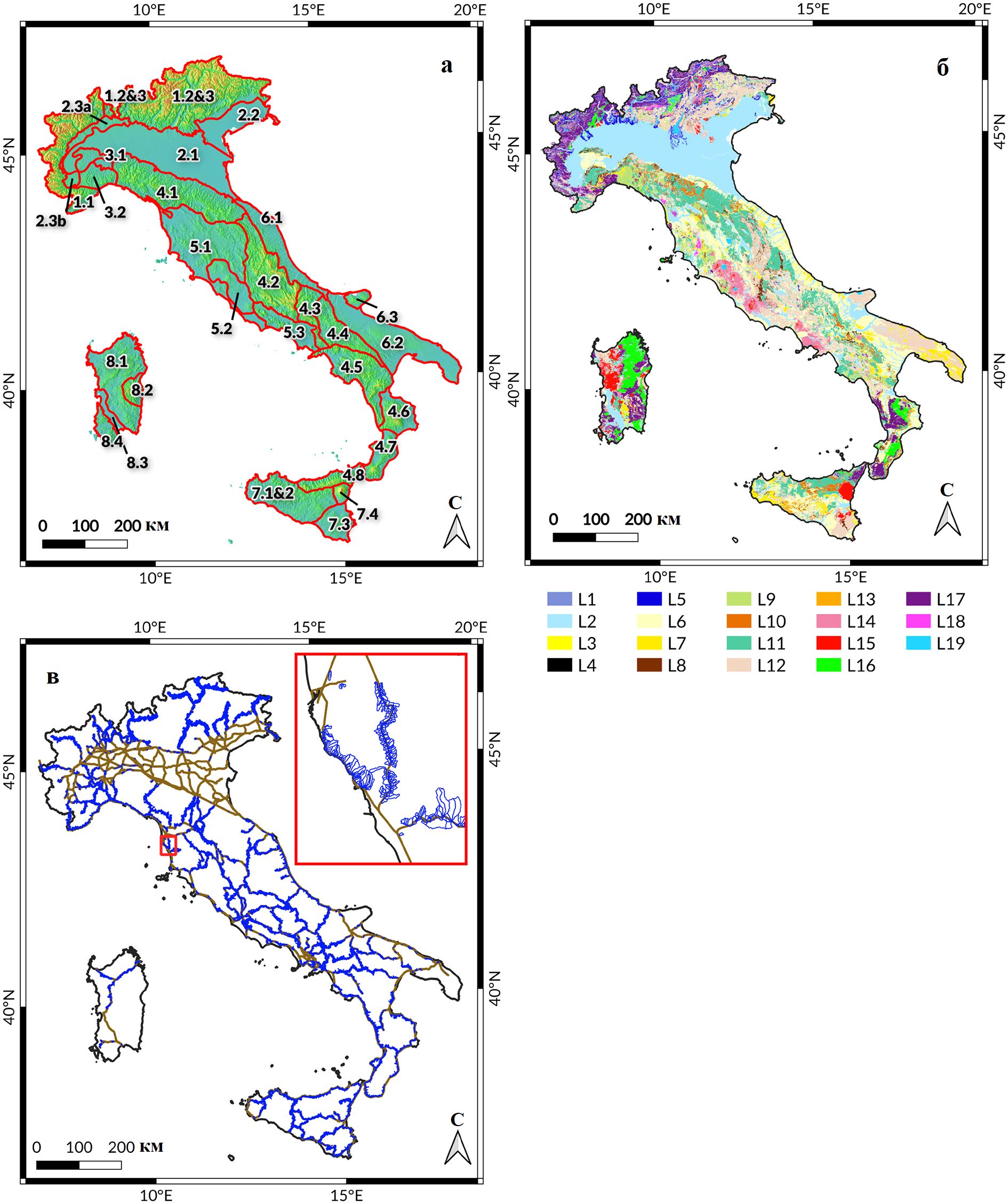
Рис. 1. Карты, использованные в работе [1]: a – карта рельефа, основанная на модели  EU-DEM («Склоновые единицы на ЦМР») с разрешением 25 м, на которой красными линиями показаны также границы 29 топографических единиц Италии, которые впервые выделили Гуццетти и Райхенбах (Guzzetti, Reichenbach, 1994), с красными линиями, наложенными на затененный рельеф, рассчитанный по EU-DEM с разрешением 25 м (по Alvioli et al, 2020а); цифровые обозначения этих топографических единиц расшифрованы в таблицах 3 и 4, а их названия будут перечислены в статье позже; карта представлена в системе координат EPSG:4326, высоты – в EPSG:3035; б – литологическая карта (буквенно-цифровые обозначения литологических классов расшифрованы в таблице 1 (по Fongo, 2018; Bucci et al., 2021)); в – принятые в этой работе [1] пространственные буферы вдоль сети железных дорог Италии, состоящие из подмножества склоновых систем (по Alvioli et al., 2020a), пересекающих буферные зоны шириной 1 км с каждой стороны железнодорожных путей, показанных коричневым цветом; склоновые системы выделены синим цветом; общее количество выбранных склоновых систем составляет 32 200 из более чем 330 000 полигонов на планиметрической площади 25 400 км² (см. таблицу 3)

Таблица 1. Значения параметров, используемых в модели STONE

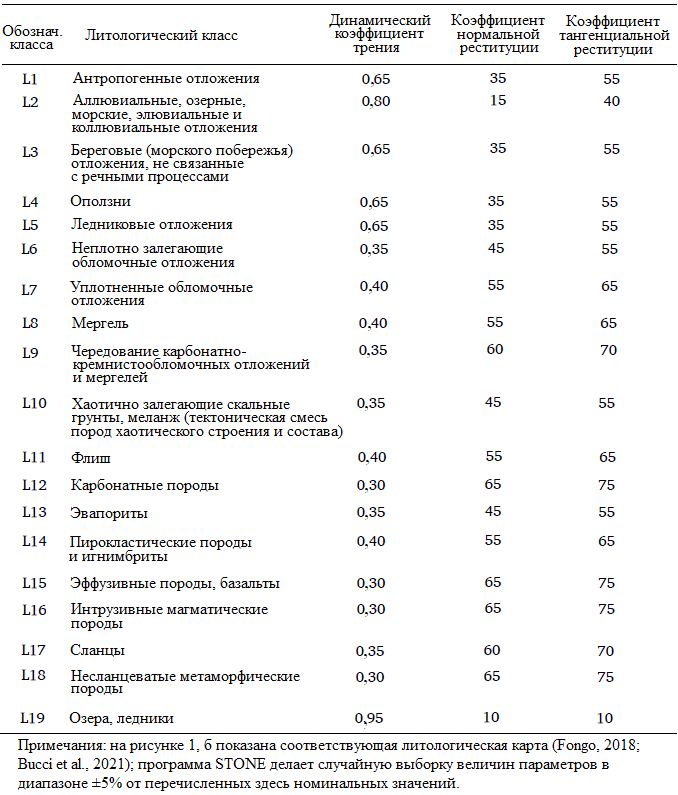
Таблица 2. Распределение сети железных дорог по интервалам высот

МЕТОДЫ РАБОТЫ

Выполнение общенациональной оценки подверженности камнепадам участков железнодорожной сети требовало тщательного планирования. Длинные цепочки действий (от выбора данных до подготовки окончательной карты) на самом деле склонны к распространению ошибок, возникших на ранних стадиях, непредсказуемым образом. Выбор STONE в качестве программного обеспечения для моделирования камнепадов (Guzzetti et al., 2002; Agliardi, Crosta, 2003) был продиктован необходимостью найти компромисс между четко определенной взаимосвязью источников с траекториями движения камнепадов и общей потребностью в вычислениях.

Чтобы создать карту подверженности камнепадам на основе результатов моделирования в STONE, авторы работы [1] предприняли следующие шаги (рис. 2):

1) подготовка данных;

2) выбор возможных зон источников, что, вероятно, является наиболее важной входной информацией для моделирования;

3) выполнение программы;

4) сбор и классификация результатов анализа подверженности камнепадам сегментов железных дорог с точки зрения свойств железнодорожной сети.

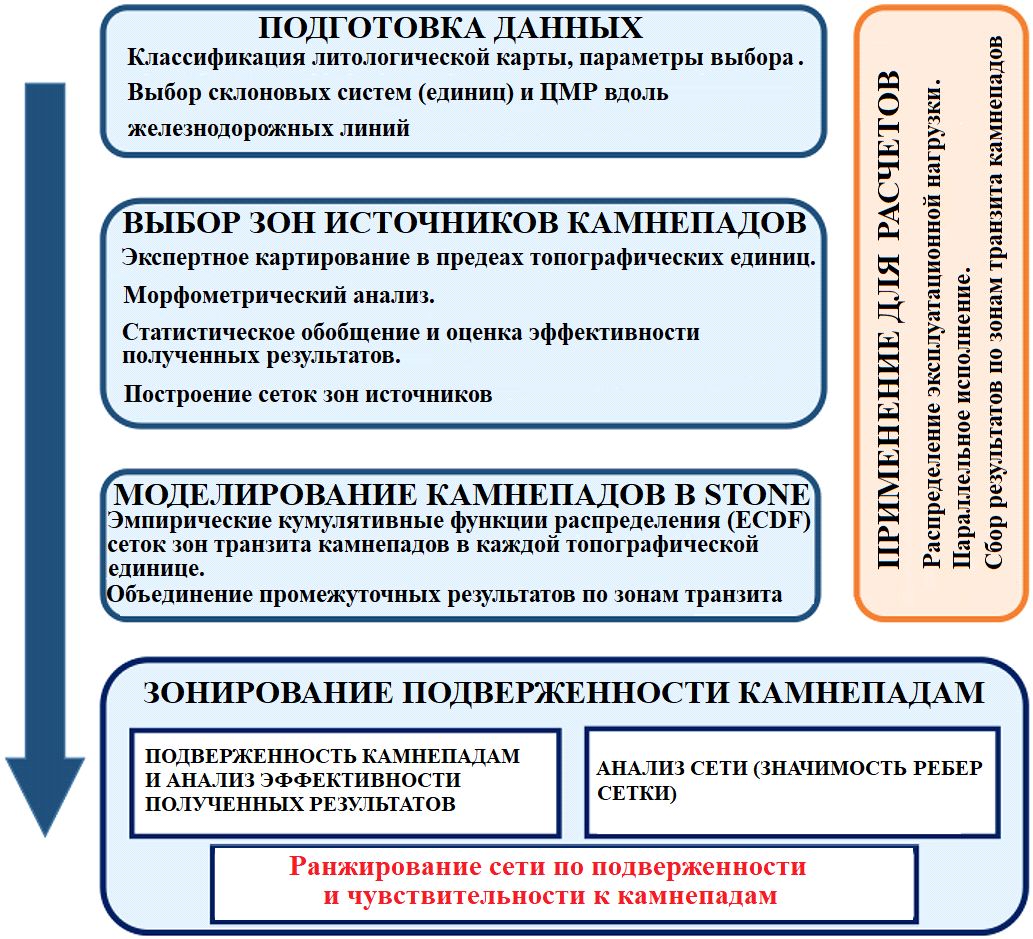
Рис. 2. Блок-схема процедуры, использованной в данной работе [1] для получения карты ранжирования сети по подверженности и чувствительности к камнепадам

Подготовка данных

Авторы работы [1] приняли подразделение на топографические единицы (ТЕ), которое ранее выполнили Гуццетти и Райхенбах (Guzzetti, Reichenbach, 1994), но немного модифицированное для разграничения склоновых единиц (Alvioli et al., 2020a). Исходное подразделение содержало 30 ТЕ, полученных путем количественного анализа и визуальной интерпретации морфометрических переменных, полученных по цифровой модели рельефа. В модифицированной версии авторы статьи [1] пренебрегли топографическими единицами, которые были намного меньше окружающих, а одну из исходных разделили на две. В итоге было получено 29 ТЕ (см. рис. 1, а). Применение топографических единиц было продиктовано потребностью в выделении сходных типов рельефа, позволяющих использовать для численного моделирования одни и те же параметры грунта в каждой ТЕ.

Использование топографических доменов также позволило определить потенциальные источники камнепадов с помощью статистического обобщения, предложенного в этой работе [1] и выполнявшегося отдельно для каждой из 29 топографических единиц, соответствующих 29 различным типам рельефа. Литологическая карта Италии в масштабе 1:100 000 предоставила необходимую информацию для определения разных наборов входных параметров для программы STONE для различных литологических классов. Эти параметры определяют поведение камней во время качения или ударов о поверхность грунта и отскоков вдоль смоделированных траекторий их движения. Окончательные значения параметров были получены с использованием результатов предыдущих исследований.

Было принято гораздо более мелкое деление территории для тех склоновых единиц, которые пересекались железнодорожными путями. Использование склоновых единиц было, с одной стороны, вполне естественным выбором, поскольку они являются картографическими единицами, хорошо подходящими для изучения оползней (Alvioli et al., 2016; Camilo et al., 2017; Schlogel et al., 2018; Bornaetxea et al., 2018; Tanyas et al., 2019a, 2019b; Jacobs et al., 2020; Amato et al., 2020; Chen et al., 2020; Li, Lan, 2020), а с другой стороны, это было решением технической проблемы определения значимых участков для параллельного выполнения моделирования.

Более конкретно, авторы приняли склоновые единицы вместо геометрической буферной зоны по бокам железнодорожной трассы, потому что траектории камнепадов, инициированные в данной склоновой единице, будут ею же и ограничены с достаточной степенью уверенности. Использованный здесь набор склоновых единиц был специально рассчитан и оптимизирован для всей Италии (Alvioli et al., 2020a) как для этой работы [1], так и для ряда дополнительных работ по выбору зон источников потоков обломочного материала (Marchesini et al., 2020) и участков, подверженных оползням дисперсных грунтов (еще не опубликовано) вдоль сети железных дорог. Набор склоновых единиц, выбранный для этой работы, показан на рисунке 1 в. Общая площадь выбранных полигонов составляет 25 400 км².

Авторы статьи [1] подготовили все данные, разбив исследуемые области на подобласти и проведя для последних параллельные расчеты. В частности, для каждой группы склоновых единиц было подготовлено независимое моделирование в STONE. Этот шаг требует выбора соответствующей части цифровой модели рельефа, зон источников камнепадов и сеток, содержащих численные значения параметров, необходимых для STONE (см. таблицу 1).

Выявление зон источников камнепадов

Определение потенциальных источников камнепадов является ключевым этапом физически обоснованного моделирования зон транзита камней (поскольку источники существенно влияют на движение).

Детальное изучение мест расположения потенциальных источников камнепадов требует экспертного анализа крутых склонов в районе исследования (Guzzetti et al., 2004; Santangelo et al., 2019, 2020), что обычно является трудоемкой и дорогостоящей процедурой. Это делает выявление потенциальных источников ограничивающим фактором для систематичных исследований камнепадов на больших территориях. Картирование всех потенциальных источников с помощью интерпретации аэрофотоснимков по всей сети железных дорог Италии было бы невозможно в разумные сроки. Более того, после обнаружения на ЦМР потенциального источника надо определить вероятность того, что это место может стать началом камнепада.

Простой способ выбора зон источников для STONE заключается в установлении порогового угла наклона поверхности, при превышении которого любая ячейка сетки действует как потенциальный источник камнепада (Guzzetti et al., 2003). Другие критерии основаны либо на сочетании геоморфологического анализа и анализа закартированных источников (Agliardi, Crosta, 2003), либо на сочетании анализа пороговых углов наклона поверхности и геоморфологического анализа (Sarro et al., 2020), либо на многофакторном статистическом анализе (Rossi et al., 2021).

Авторы работы [1] определили места расположения источников камнепадов и величины вероятности разрушения для большой площади по TINITALY – цифровой модели рельефа Италии с разрешением 10 м (Tarquini et al., 2007), для чего выполнили следующие этапы работ:

1а) выбор буферной зоны шириной 1 км с каждой стороны от трассы железнодорожного пути;

2а) выбор подмножества склоновых единиц, пересекающихся с буферной зоной, из всего их набора, включающего в Италии около 330 000 склоновых единиц по расчетам Альвьоли и др. (Alvioli et al., 2020а);

3а) экспертное картирование зон потенциальных источников камнепадов в пределах выбранных склоновых единиц для выборки мест, которые были сочтены репрезентативными по условиям, способным спровоцировать камнепады в отдельной топографической единице (Guzzetti, Reichenbach, 1994);

4а) разработка процедуры, основанной на данных, для идентификации зон источников в разных ячейках сетки среди закартированных зон (рис. 3, а) в пределах одной и той же топографической единицы с использованием статистического обобщения;

5а) визуальный анализ карты источников камнепадов, полученной в результате выполнения пункта 4а, и включение в нее дополнительных источников, выявленных экспертным путем.

Выбор склоновых единиц, пересекающихся с 1-километровой буферной зоной с каждой стороны от трассы железнодорожного пути (см. выше пункт 1а), гарантирует, что в моделировании будут учтены все потенциальные источники, в которых могут возникнуть камнепады, способные навредить железнодорожной сети (в этой работе [1] не учитываются какие-либо антропогенные смещения грунтовых масс вблизи железнодорожных путей).

Экспертное картирование было выполнено на основе изображений, полученных на сервисе Google Earth™, которые были выбраны потому, что они одновременно предоставляют и морфологическую (по высотам), и оптическую информацию, в результате чего получаются 2,5D изображения. Они менее точны, чем стереоскопические оптические изображения, но их преимуществами являются полнота и свободный доступ к ним в национальном масштабе. Это гораздо лучше, чем использование 2D изображений из геоинформационных систем (ГИС), также находящихся в свободном доступе, но не содержащих морфологической информации. Инструмент редактирования в векторном формате позволяет непосредственно выполнять картирование на интерпретированных изображениях и экспортировать полученные полигоны.

Чтобы нанести на карту зоны потенциальных источников камнепадов, геоморфологи решили, что они соответствуют субвертикальным скальным склонам, под которыми видны осыпи или отложения камнепадов. Обычно они кажутся не покрытыми растительностью, даже если в некоторых местах высокая растительность может скрывать потенциальные участки отрыва каменного материала от поверхности. Для каждой топографической единицы геоморфологи нанесли на карту все зоны потенциальных источников камнепадов в пределах каждой склоновой единицы в значительном подмножестве склоновых единиц, которые считались репрезентативными для основных структурно-литологических и морфологических условий.

В работе [1] использовалась информация об источниках, нанесенных на карту экспертами, для расчета вероятности того, что та или иная ячейка сетки является источником, следующим образом. Для топографической единицы выбирались склоновые единицы, содержащие нанесенные на карту полигоны. Были рассчитаны гистограммы распределения значений угла наклона поверхности в ячейках внутри полигонов и в пределах всей склоновой единицы. Для каждого столбика гистограммы шириной 2 град. (интервала увеличения наклона поверхности величиной 2 град.) бралось отношение двух гистограмм – значений углов наклона в пределах зон источников к их значениям в пределах целых склоновых единиц. В каждом указанном интервале значения числителя были меньше значений знаменателя (количество ячеек из зон источников, попавших в каждый 2-градусный интервал, было меньше или равно числу ячеек из целой склоновой единицы в том же интервале). Поскольку авторы статьи [1] позаботились о том, чтобы разграничить все зоны возможных источников камнепадов в пределах каждой из рассматриваемых склоновых единиц, они были уверены, что это отношение представляет собой вероятность того, что та или иная ячейка с углом наклона поверхности, характерным для соответствующего интервала величиной 2 град., является источником камнепадов в этой конкретной склоновой единице. Таким образом, имелась точка вероятности для каждого 2-градусного интервала наклона. Рассмотрев все выбранные склоновые единицы в данной топографической единице, авторы работы [1] в итоге получили набор вероятностей, показанных зелеными точками на рисунке 3, для топографической единицы 1.2&1.3 (см. рис. 1, а), выбранной в качестве иллюстративного примера.

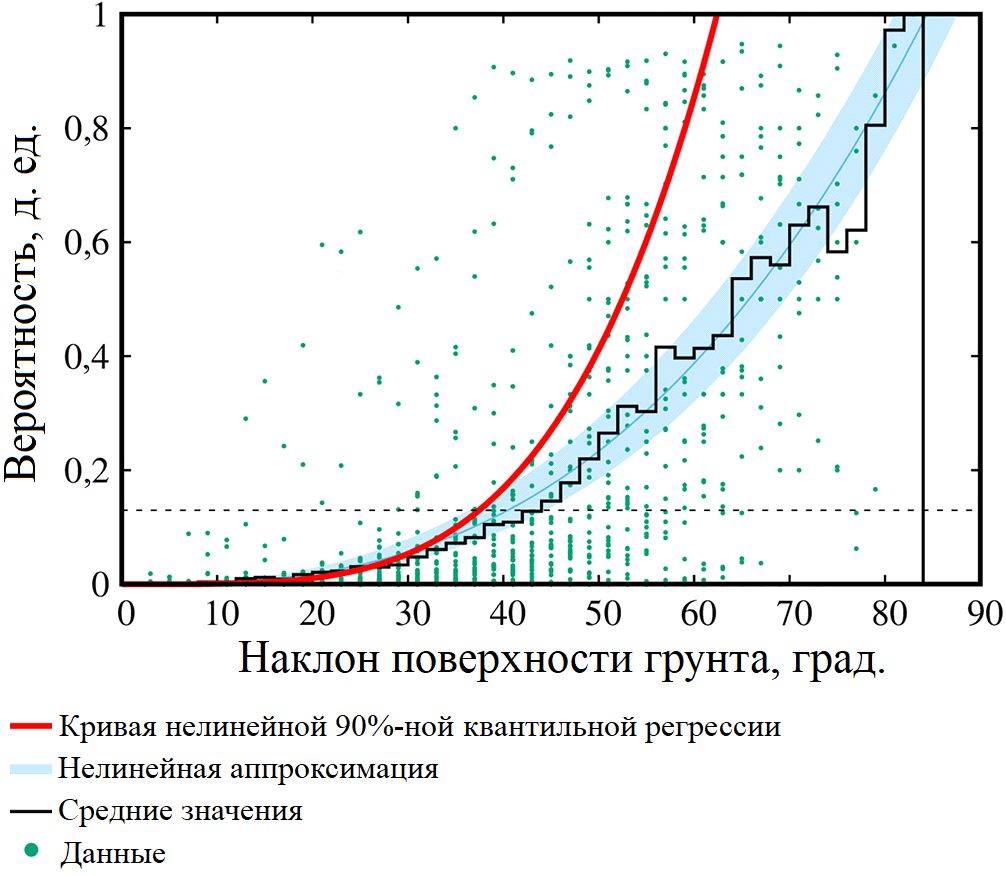
Рис. 3. Пример результата статистической оценки вероятности того, что ячейка сетки с данным уклоном представляет собой зону источника камнепадов. Данные (зеленые точки) и численные модели (кривые) соответствуют топографической единице 1.2&1.3 (см. рис. 1, а). Принятой моделью является кривая нелинейной 90%-ной квантильной регрессии, соответствующая уравнению (2), которая показана красным цветом. Горизонтальная линия представляет собой предел, ниже которого вероятность устанавливается равной нулю

Целью этой процедуры было получение зависимостей «вероятность – наклон», которые можно было бы распространить на все множество выбранных склоновых единиц в каждой топографической единице. На рисунке 3 зеленые точки соответствуют вероятностям из экспертного картирования, а кривые представляют три возможных подхода к определению функциональной зависимости между вероятностью и наклоном. Черная гистограмма показывает простые средние значения наблюденных значений вероятности для каждого 2-градусного интервала наклона. Синяя кривая представляет собой нелинейную аппроксимацию значений вероятности, оцененных по наблюденным данным, которую описывает следующая функция:

где S – наклон поверхности в градусах; a, b – параметры аппроксимации.

Голубая полоса вокруг синей кривой аппроксимации на рисунке 3 представляет собой зону между минимальной и максимальной кривыми, полученными с использованием параметров аппроксимации a±σ_a и b±σ_b (где σ_a, σ_b – стандартные отклонения, полученные путем минимизации методом наименьших квадратов). Эта полоса показана для иллюстрации качества аппроксимации. Красным цветом на рисунке 3 показана кривая нелинейной квантильной регрессии для 90-го процентиля (квантиля), которая описывается следующей функцией, содержащей один параметр c:

Уравнение (2) описывает кривую, делящую наблюдаемую выборку таким образом, что 10% зеленых точек на рисунке 3 оказываются выше этой кривой.

Было решено использовать метод квантильной регрессии (формулу (2)), чтобы назначить вероятность того, что та или иная ячейка сетки представляет собой зону источника камнепадов (см. пункт 4а в списке этапов работ, приведенном ранее). С точки зрения авторов работы [1], это максимизирует информацию, извлеченную из наблюденных данных, по отношению к среднему значению и аппроксимации по уравнению (1). Кроме того, авторы использовали функцию с фиксированным показателем степени для (S/90), равным 4, поскольку при использовании параметрического показателя степени b, как в уравнении (1), полученные кривые систематически занижали вероятность присутствия источника камнепадов при больших наклонах поверхности. Принятая процедура обеспечивает индивидуальную кривую P_QR(S) для каждой топографической единицы, полученную с помощью экспертного картирования зон потенциальных источников камнепадов и нелинейной квантильной регрессии вероятностей, наблюденных в одной и той же топографической единице.

В каждой топографической единице «поячеечные» (cell-by-cell) значения вероятности, полученные из уравнения (2), были напрямую связаны с количеством смоделированных траекторий при рассмотрении ячейки как начальной точки падения камня. Авторы работы [1] ввели более низкую пороговую вероятность, при которой ячейка не рассматривалась как источник. Этот порог представляет собой минимум между значением P_QR для карты зон источников, охватывающей не менее 80% источников, нанесенных на карту с помощью визуальной интерпретации, и значением P_QR=10%. Авторы моделировали для каждой ячейки-источника ряд траекторий, соответствующих численному значению P_QR в процентах (например, ячейка с вероятностью X% вызвала бы инициацию X смоделированных траекторий). Это позволяет использовать возможности STONE для моделирования различных количеств падающих камней на основе вероятности того, что данная ячейка является источником. Этот метод увеличивает степень рандомизации (случайности) в моделях (вместе со случайным выбором значений входных параметров в пределах заданного процента вокруг среднего значения).

В конце концов, авторы статьи [1] оценили степень соответствия между моделью и реальностью, используя частоту совпадений (hit rate), то есть долю достоверных результатов моделирования, определяемую формулой HR=TP/(TP+FN), где TP – количество достоверных результатов (true positives), FN – число ложных результатов (false negatives). С учетом того, что TP+FN=P (где P – общее количество попыток сделать прогноз), значение HR – это доля случаев, когда прогноз был удачным, от общего числа попыток.

Моделирование траекторий камнепадов с помощью STONE

После выбора зон источников были предприняты следующие шаги для расчета подверженности территорий камнепадам в пределах полигональной буферной зоны вокруг всей сети итальянских железных дорог с использованием программы STONE и цифровой модели рельефа с разрешением 10 м, использованной для определения источников камнепадов:

1б) присвоение значений коэффициентов динамического трения, коэффициентов нормальной и тангенциальной реституции, необходимых для работы в программе STONE (этот шаг был выполнен путем экспертного присвоения значений коэффициентов, взятых из литературы для каждого литологического класса);

2б) подготовка сеток данных, необходимых для работы STONE в пределах каждой топографической единицы, с последующим разделением на прямоугольные домены, содержащие смежные полигоны склоновых единиц, выбранные на этапе 2а, описанном в предыдущем подразделе);

3б) создание актуальных моделей с помощью STONE (в работе [1] параллельно были выполнены имитации, распределенные в 921 подобластях, описанных в пункте 2б);

4б) сбор данных по различным растровым картам, содержащим информацию о количестве траекторий падающих камней на ячейку сетки (counter – «счетчик»), в каждой из подобластей каждой из 29 топографических единиц;

5б) преобразование (классификация) «карты-счетчика» в вероятностную карту.

Для работы в программе STONE необходимы значения коэффициентов динамического трения, тангенциальной и нормальной реституции (см. пункт 1б). Они были выбраны следующим образом. Была рассмотрена литологическая карта масштаба 1:100 000, полученная из цифровой (электронной) карты в векторном формате. Исходная карта Итальянской геологической службы (ISPRA) (Tacchia, 2004; Battaglini et al., 2012) содержала более 5000 уникальных описаний геологических формаций (Fongo, 2018; Bucci et al., 2021). Исходное уникальное описание было разделено (классифицировано) на 19 литологических классов с использованием экспертных критериев и примерно 400 листов геологической карты (цифровых фотографий из того же источника) в более крупном масштабе. Значения вышеуказанных коэффициентов для работы в программе STONE были получены с использованием предыдущих оценок для аналогичных литологических условий, приведенных в литературе (Guzzetti et al., 2002, 2003, 2004; Agliardi, Crosta, 2003; Santangelo et al., 2019). Выбранные значения коэффициентов перечислены в таблице 1.

Шаги 2б, 3б и 4б были выполнены для 921 подобласти, выделенной путем отдельного рассмотрения для групп смежных склоновых единиц, на основе:

1) цифровой модели рельефа исследуемой подобласти;

2) сетки, содержащей положения зон источников камнепадов с указанием количества траекторий камней, которые необходимо смоделировать;

3) трех сеток, содержащих значения коэффициентов динамического трения, нормальной и тангенциальной реституции для каждой ячейки сетки ЦМР.

Программа STONE создает в качестве выходных данных три сетки, содержащие для каждой ячейки:

а) подсчет количества траекторий, которые пересекли ячейку во время моделирования;

б) максимальную высоту траекторий относительно местной высотной отметки;

в) максимальную скорость моделируемого движения камней.

В принципе, эти три сетки можно использовать совместно для оценки опасности камнепадов в каждой ячейке. На самом деле, для заданных зон источников пункт (а) можно интерпретировать как относительную вероятность того, что та или иная траектория пересечет каждую ячейку сетки, а пункты (б) и (в) можно совместно рассматривать как показатель величины ожидаемых камнепадов в каждой ячейке. Вместо этого для оценки частоты камнепадов (во времени) требуется дополнительная информация (Guzzetti et al., 2003, 2004). В этой работе [1] авторы использовали только выходные данные из пункта (а) – в качестве оценки относительной пространственной вероятности камнепадов.

Чтобы преобразовать количество траекторий на ячейку в показатель вероятности (см. шаг 5б), авторы статьи [1] использовали следующее обоснование. Они рассмотрели реестр национальной инвентаризации оползней Италии IFFI (ISPRA, 2018; Trigila et al., 2010) и «извлекли» полигоны, помеченные как «камнепады» или как «большие территории, содержащие камнепады». Далее были рассчитаны эмпирические кумулятивные функции распределения (ECDF) количеств траекторий в пределах ячеек сетки, принадлежащих полигонам, извлеченным из вышеуказанного реестра. Значимыми считались только те ячейки, о которых было известно, что они действительно содержат камнепад/камнепады. Авторы работы [1]  использовали ECDF (в интервале [0, 1]) для подчета траекторий с ненулевым значением для картирования всех ячеек сетки, что позволило выполнить вероятностную интерпретацию, необходимую для создания карты подверженности камнепадам.

Использование ECDF вместо простого нормирования количеств траекторий имеет два преимущества. Во-первых, это позволяет приписать меньшую значимость ячейкам с небольшим числом траекторий, учитывая огромную дисперсию их количеств в сетках на выходе. Во-вторых, применение ECDF делает результаты независимыми от абсолютных количеств смоделированных траекторий на исходную ячейку сетки и делает значимыми только относительные величины в соответствии с методом присвоения этих чисел, использованным авторами статьи [1] (см. подраздел «Выявление зон источников камнепадов»). Отдельно для каждой из 29 топографических единиц (см. рис. 1, а; таблицу 1) было выполнено преобразование подсчитанной вероятности в относительную. На рисунке 4 показаны примеры ECDF, полученные для четырех топографических единиц.

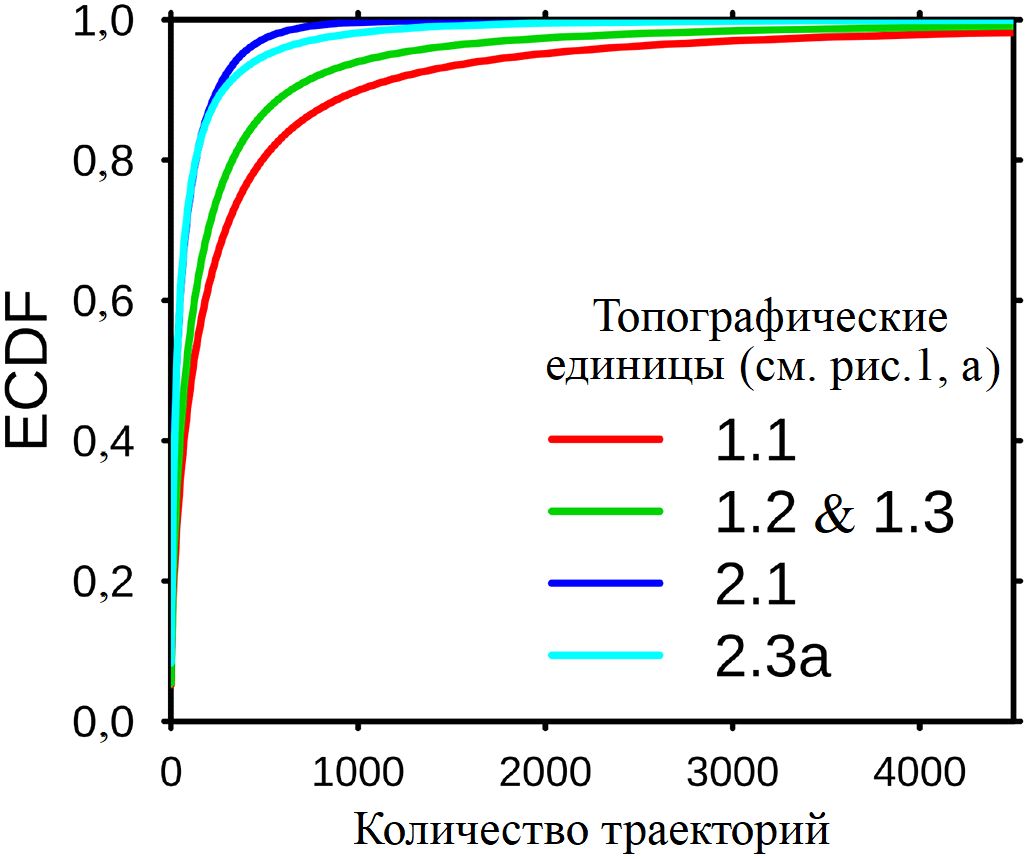
Рис. 4. Примеры эмпирических кумулятивных функций распределения (ECDF), полученных для четырех топографических единиц [1]

Анализ железнодорожной сети в рамках теории графов

Железнодорожную сеть можно рассматривать как набор раздельных пунктов (узлов, пересечений) и связывающих смежные пункты перегонов (звеньев), не имеющих пересечений. От узлов может отходить несколько звеньев. Этот набор представляет собой географическую сеть. Ее описание можно дополнительно уподобить графу, вершины которого являются узлами сети, а ребра – ее звеньями.

Авторы статьи [1] выполнили простой предварительный анализ графа, соответствующего железнодорожной сети Италии, рассчитав центральность по промежуточности (степень посредничества) для всех вершин и ребер. Такой анализ описывает топологию графа и является отправной точкой для обсуждения чувствительности железнодорожной сети к камнепадам в связи с интенсивностью ее работы. Его графическое представление показано на рисунке 5, где вершины соединены прямыми линиями – ребрами графа. Цвета точек и ребер соответствуют низкой средней или высокой степени посредничества. А толщина ребер примерно пропорциональна физическому расстоянию между узлами, которые они соединяют. Известно, что центральность ребер по промежуточности во взвешенном графе является одной из наиболее важных переменных в сетях (Barthelemy, 2011), поэтому авторы работы [1] использовали ее в последующем анализе.

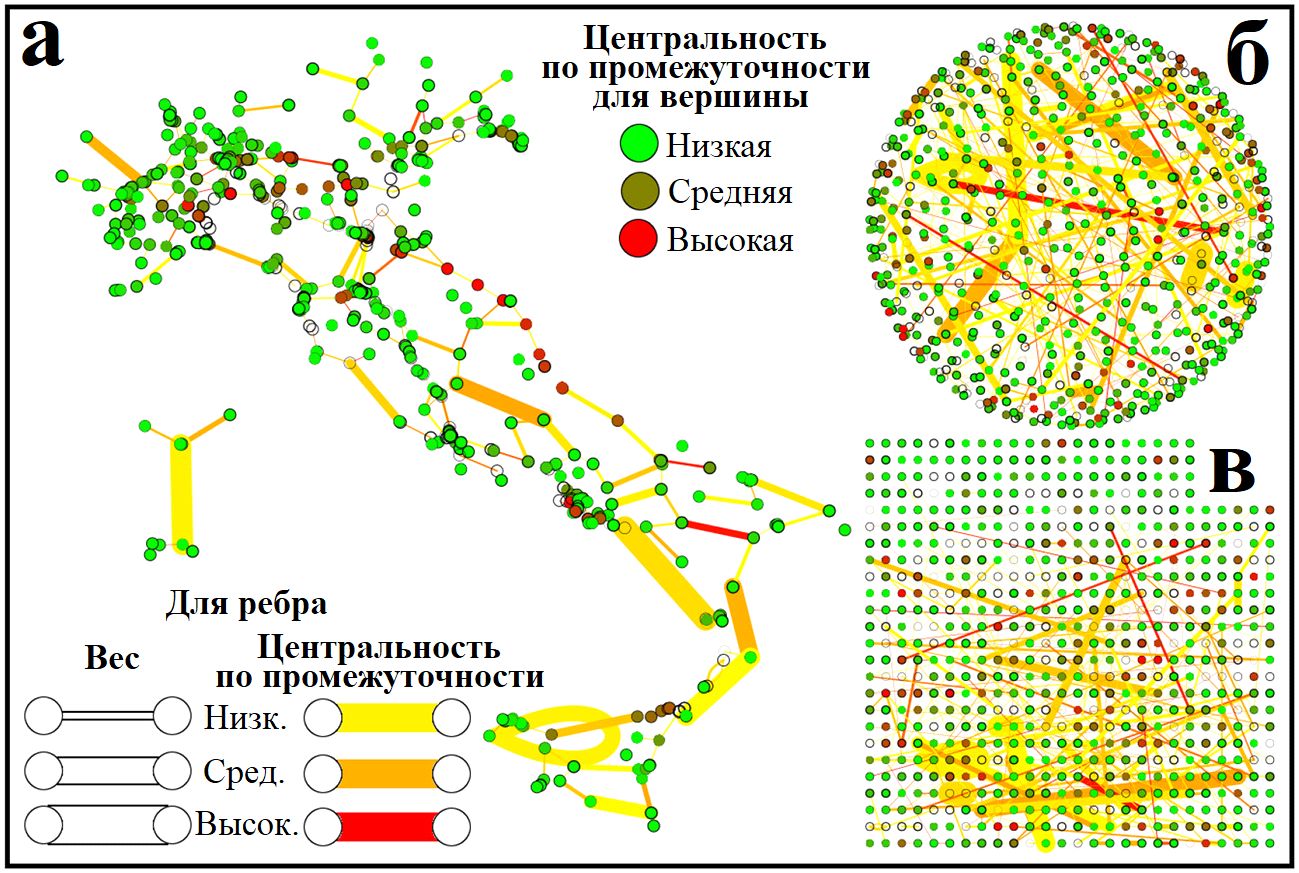
Рис. 5. Три представления железнодорожной сети Италии в виде графов с одинаковой информативностью: а – пространственное распределение вершин (кружков) соответствует их географическому положению, звенья (перегоны) сети условно представлены в виде прямых линий (ребер), соединяющих вершины; б, в – два альтернативных представления одного и того же графа: б – узлы равномерно распределены по поверхности сферы; в – узлы расположены по квадратной сетке (видно, что узлы в большинстве своем являются скорее периферийными). Разных представлений одного и того же графа, в принципе, может быть сколько угодно, но при этом какое-либо конкретное представление может помочь выделить какие-то особые аспекты

Чтобы в рамках теории графов понять влияние возможных камнепадов на перебои в работе железнодорожной сети, авторы статьи [1] провели два отдельных анализа. Во-первых, было рассмотрено влияние на граф (и, соответственно, на реальную сеть) удаления из сети одного за другим ребер (то есть железнодорожных перегонов, состоящих из переменного числа 1-километровых сегментов). Во-вторых, совместно с этим было рассмотрено подразделение (классификация) перегонов железной дороги на классы по их подверженности камнепадам и по их значимости в эквивалентном графе.

При удалении одного ребра из графа для всех оставшихся ребер немного изменяются величины их центральности по промежуточности. Для каждого ребра в графе была рассчитана полная вариация (изменение) между исходным графом и графом, полученным при удалении одного ребра, и ее значение присваивалось в качестве атрибута удаленному ребру в исходном графе. Авторы статьи [1] "перебрали" таким образом весь набор ребер, получив в итоге их новое ранжирование в соответствии с их вновь вычисленными атрибутами. Эти атрибуты использовались в качестве дополнительных показателей для комбинированной классификации железнодорожной сети, основанной как на подверженности, так и на чувствительности к камнепадам.

Вычислительная реализация

Моделирование для большой территории с помощью STONE имеет следующее ограничение. Эта программа серийно вычисляет заданное пользователем число траекторий. Несмотря на то что каждый расчет выполняется относительно быстро, большое количество траекторий, необходимых для этого исследования, сделало бы невозможным выполнение всех вычислений за один этап. Для решения этой проблемы авторы работы [1] приняли простую стратегию, разделив изучаемые области на множество подобластей (на группы смежных склоновых единиц) и параллельно запустив в работу несколько экземпляров STONE (см. подраздел «Моделирование траекторий камнепадов с помощью STONE»).

Для каждой подобласти автоматически были подготовлены растровые сетки с помощью геоинформационной системы для обработки пространственной информации GRASS (Geographic Resources Analysis Support System) (Neteler, Mitasova, 2007; Casagrande et al., 2007). Авторы данной статьи [1] использовали многоядерный процессор, имеющий 48 вычислительных ядер и 330 ГБ оперативной памяти, для параллельного выполнения ГИС-операций, необходимых для подготовки сеток, выполнения самой программы и сбора 921 субрезультата (см. соответственно пункты 2б, 3б и 4б в подразделе «Моделирование траекторий камнепадов с помощью STONE»). Общее время выполнения каждого полного «прогона» составило около двух дней при использовании схемы «главный – подчиненный», или «ведущий – ведомый» (схемы взаимодействия в вычислительных комплексах, информационных и телекоммуникационных системах, в которой одно главное (ведущее) устройство, процесс или их группа осуществляет однонаправленное управление подчиненным (ведомым) устройством, процессом или их группой. – Ред.). Такая схема могла наилучшим образом сбалансировать рабочую нагрузку.

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

Результаты определения зон источников камнепадов

Процедура, описанная в подразделе «Выявление зон источников камнепадов», применялась к каждой из топографических единиц, принятых в этой работе в качестве однородных доменов для моделирования с помощью STONE. На рисунке 6 показаны зависимости вероятностей камнепадов от наклона поверхности почти для всех топографических единиц (графики для топографической единицы 1.2&1.3 были показаны на рисунке 3). После оценки зон источников и связанных с ними вероятностей камнепадов авторы работы [1] визуально проверили отсутствие явных ошибок для территорий вдоль всех железнодорожных линий. Систематически проверялись результаты статистической классификации источников вдоль всей железнодорожной сети с помощью экспертного визуального анализа. В нескольких выбранных местах, в которых, как сочли опытные геоморфологи, инфраструктура потенциально подвержена явному риску, были оконтурены дополнительные зоны источников. В таблице 3 для каждой топографической единицы указаны: общая площадь, площадь рассматриваемых склоновых единиц, количество и общая площадь закартированных экспертами полигонов из ячеек сетки с потенциальнми источниками камнепадов.

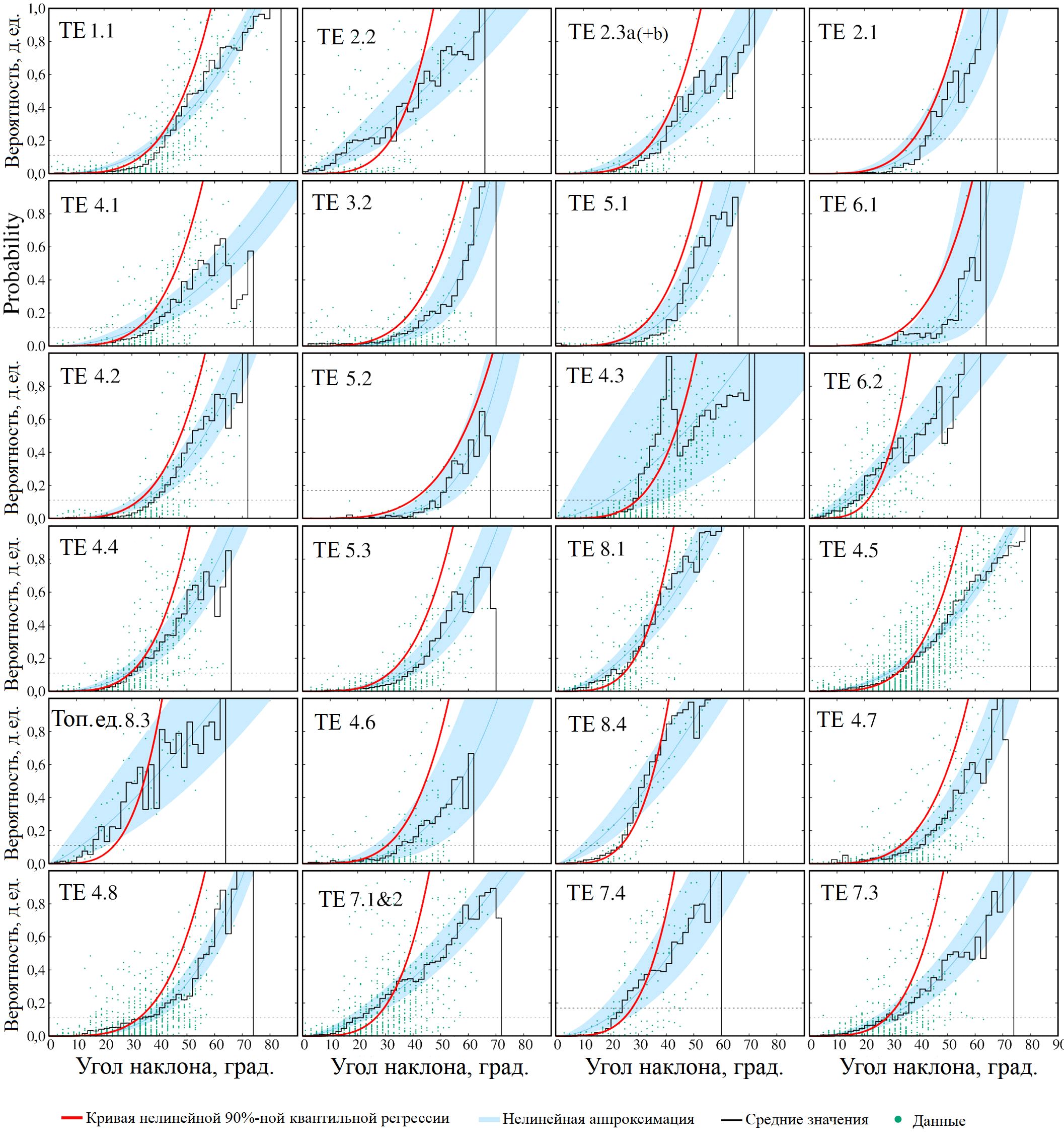
Рис. 6. Зависимости вероятностей камнепадов от наклона поверхности почти для всех топографических единиц (ТЕ, см. рис. 1, а). Графики для топографической единицы 1.2&1.3 показаны на рисунке 3. Данные, касающиеся зон источников, для ТЕ 2.3а и 2.3б сгруппированы на одной панели. Для топографической единицы 3.1 нет данных по закартированным зонам источников, а для 6.3 и 8.2 нет пересечений между железной дорогой и склоновыми единицами, поэтому соответствующие три панели отсутствуют на данном рисунке

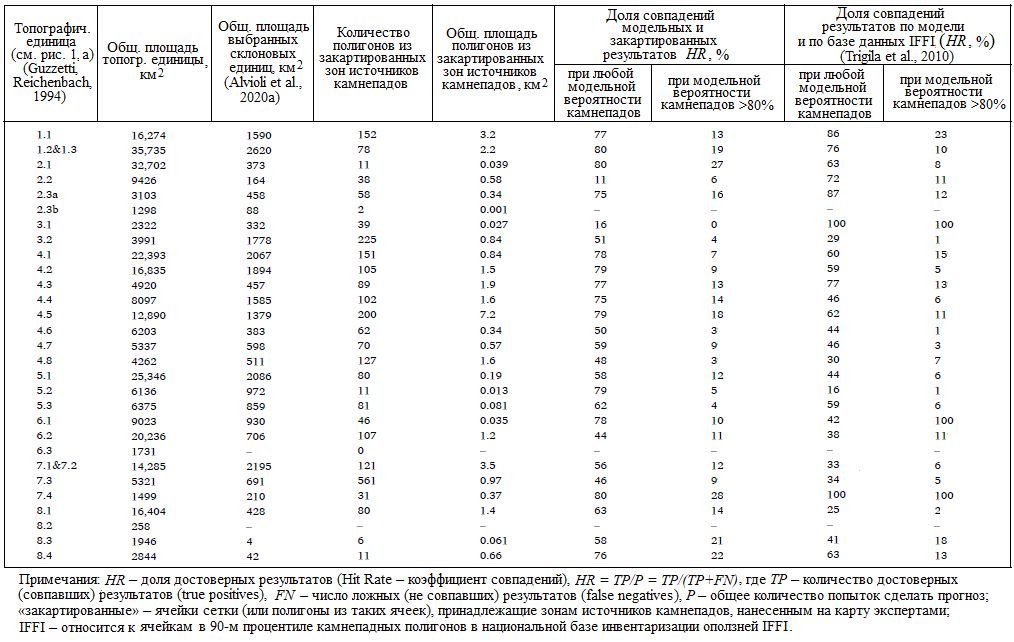
Таблица 3. Результаты статистического обобщения для определения вероятностей того, что ячейки сетки инициируют траектории камнепадов

Из-за большой площади исследуемой территории авторы статьи [1] в иллюстративных целях показывают детали процедуры экспертного картирования, выбора источников камнепадов и их сравнения для одной конкретной топографической единицы 1.2&1.3 (состоящей из объединенных топографических единиц 1.2 и 1.3 – Центрально-Восточных Альп и карстового плато Карсо) (Guzzetti, Reichenbach, 1994). На рисунке 7, а показан общий вид ТЕ 1.2&1.3, трасса железнодорожного пути, полигоны в пределах этой единицы, нанесенные на карту экспертами, а также часть камнепадных полигонов по национальной базе данных IFFI, перекрывающихся с набором склоновых единиц в ТЕ 1.2&1.3. Подобные условия были обнаружены на всей исследованной территории площадью около 25 000 км².

На рисунке 7, б в увеличенном масштабе показан участок (соответствующий маленькому оранжевому квадратику в правой части рисунка 7, а), содержащий  несколько склоновых единиц, расположенных на северо-востоке топографической единицы 1.2&1.3, в которых присутствуют как полигоны, нанесенные на карту экспертами, так и полигоны из базы данных IFFI. Полигоны из базы данных IFFI разделены по высотным отметкам на: основную часть; часть ниже уровня 10-го процентиля и часть выше уровня 90-го процентиля. Процентили помогают показать, что большинство камнепадных полигонов из базы данных IFFI фактически содержат как зоны источников, так и зоны транзита и отложения камнепадного материала. Отсюда авторы работы [1] заключают, что верхний процентиль относится к верху склоновых единиц и примерно соответствует источникам, закартированным экспертами, а нижний процентиль относится к подножиям склонов и тянется вниз к долине для больших полигонов. Эти характеристики были общими для всех камнепадных полигонов из базы данных IFFI, которые авторы проверяли визуально. Они использовали верхний и нижний процентили, чтобы иметь общее представление о результативности как выбора источника, так и итогов моделирования в последующем.

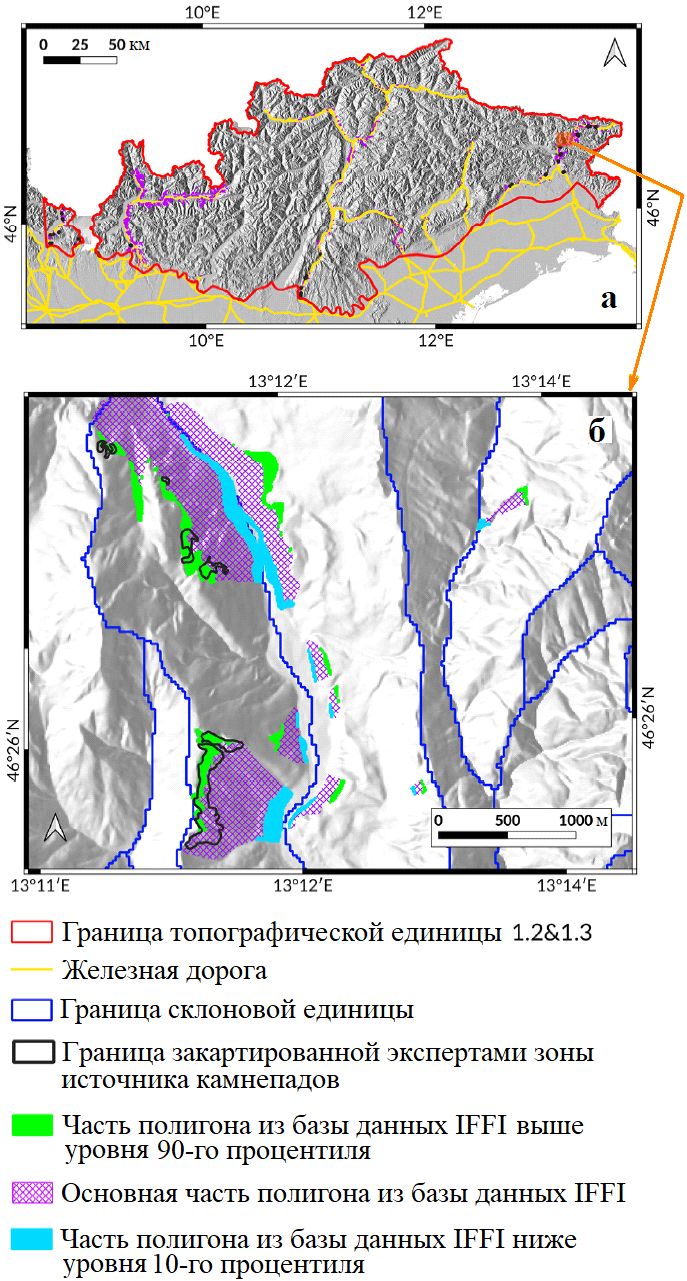
Рис. 7. Иллюстрация взаимосвязи между зонами источников камнепадов, нанесенными на карту экспертами, и информацией из национальной базы данных IFFI в пределах буферных зон с каждой стороны от трассы железнодорожного пути: а – общий вид топографической единицы 1.2&1.3; б – фрагмент, выделенный на рисунке 7, а оранжевым квадратиком, в увеличенном масштабе, показывающий несколько участков склона, на которых присутствуют как закартированные экспертами зоны источников камнепадов, так и камнепадные полигоны из базы данных IFFI (видно, что закартированные экспертами зоны источников примерно совпадают с частями полигонов из IFFI выше уровня 90-го процентиля и что части полигонов ниже уровня 10-го простираются вниз до дна долин)

Результатом обобщения является карта с сеткой 10 м x 10 м, совмещенная с цифровой моделью рельефа TINITALY. Каждой ячейке присуще определенное значение вероятности того, что траектория камнепада исходит из этого конкретного места. Пример такой вероятностной карты источников камнепадов для топографической единицы 1.2&1.3 показан на рисунке 8, а.

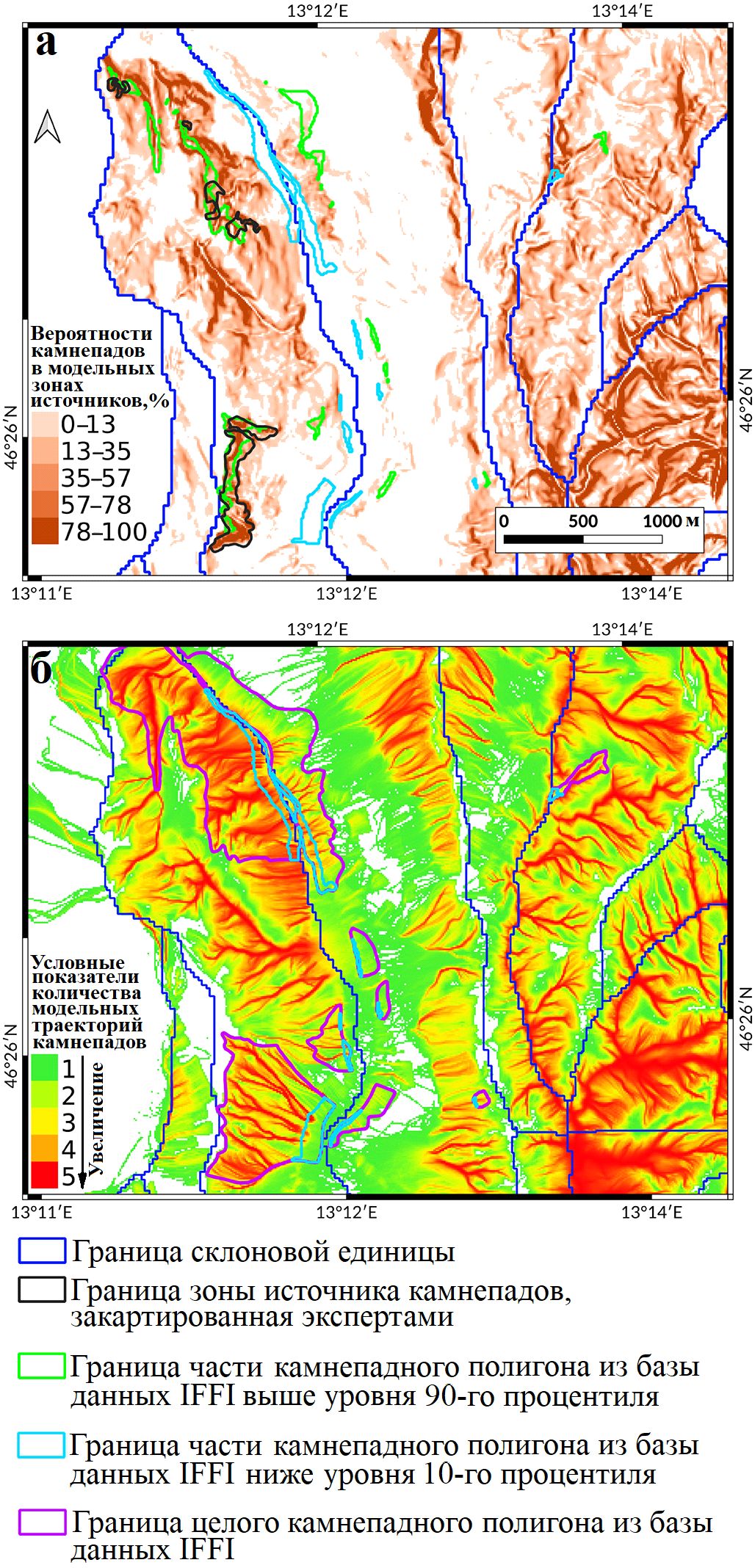
Рис. 8. Карты смоделированных зон источников камнепадов с отражением вероятностей начала в них камнепадов (а) и модельных зон с разным количеством траекторий камнепадов (б) в сопоставлении с целыми полигонами из базы данных IFFI и их частями выше уровня 90-го процентиля и ниже уровня 10-го процентиля, а также с выделенными склоновыми единицами

Сравнение смоделированных вероятностей с зонами источников камнепадов, нанесенными на карту экспертами, представляет собой оценку эффективности этапа калибровки идентификации источника. Эта эффективность определяется количеством совпадений смоделированных вероятностей с реальными данными, представленными нанесенными на карту полигонами. Авторы работы [1] рассмотрели смоделированную вероятность двумя разными способами. Они либо выбрали все ячейки сетки, для которых статистическая процедура присвоила какую-либо ненулевую вероятность, и ячейки с вероятностями больше 0,8 (величина 0,8 была произвольно выбрана в качестве порога перехода к «высоким» вероятностям).

Авторы статьи [1] разработали и второе сравнение, используя для проверки правильности идентификации источников камнепадные полигоны из базы данных IFFI (Trigila et al., 2010). Для каждого полигона из IFFI путем расчетов была выделена часть, соответствующую верхним 90% высоты. Это было, с точки зрения авторов, наилучшее произвольное предположение о возможных источниках камнепадов, зарегистрированных в IFFI.

Результаты сравнений в каждой из топографических единиц с точки зрения частоты совпадений (HR – hit rate), то есть доли достоверных результатов моделирования, перечислены в таблице 3. Авторы исследования [1] не оценивали частоту истинных несовпадений, являющуюся аналогом частоты совпадений, или полную матрицу несоответствий, из-за того, что истинные несовпадения были неизвестны, потому что экспертное картирование было выполнено только в выбранном месте. К тому же авторы не знали, отражает ли база данных IFFI полную инвентаризацию оползней и в частности камнепадов. Доли совпадений были рассчитаны для склоновых единиц, выбранных в качестве участков исследований для этой работы.

Рассмотрим распределение величин частоты совпадений HR, представленных в таблице 3, для следующих комбинаций зон в 26 топографических единицах (ТЕ) (напомним, что три из первоначальных 29 ТЕ были исключены из-за отсутствия железной дороги или склонов с предрасположенностью к камнепадам).

1. Смоделированные зоны источников с любыми ненулевыми значениями вероятности начала камнепада и закартированные экспертами зоны источников. Значения HR оказалась ниже 75% для 12 топографических единиц, таких как: 2.2 (равнина Венето), 3.1 (холмы Монферрато) , 4.6 (горное плато Сила), 4.7 (национальный парк Аспромонте в южной части Апеннинских гор), 4.8 (Сицилийские Апеннины), 5.1 (горный пояс Тирренской границы Калабрии), 7.1&7.2 (Марсалская низменность и Сицилийские холмы), 7.3 (Иблейское плато (горы)), 8.1 (Сардинские холмы) и 8.3 (равнина Кампидано). Из них 5 ТЕ имели HR<50%, а из последних 2 ТЕ (2.2 и 3.1) имели HR<25%. Соответствующие топографические единицы имеют небольшую или очень маленькую общую площадь склоновых единиц, и многие из них расположены рядом с равнинами или морскими побережьями, которые, вероятно, труднее всего моделировать на региональном или национальном уровне, поскольку они больше всего отличаются от типичных условий, в которых авторы статьи [1] картировали источники камнепадов экспертным путем.

2. Смоделированные зоны источников при включении лишь ячеек сетки с наибольшей (>80%) вероятностью начала камнепада и закартированные экспертами зоны источников. Обоснованность этого сопоставления, вероятно, труднее понять на общих основаниях. Для 4 топографических единиц оказалось, что HR>20%, 11 ТЕ имели HR<10% (причем 5 ТЕ из них имели HR<5%).

3. Смоделированные зоны источников с любым ненулевым значением вероятности начала камнепада и части камнепадных полигонов из базы данных IFFI для уровня выше 90-го процентиля по высоте (для верхних 90% высоты полигонов). Результаты показали более низкую степень совпадений по сравнению со случаем 1. Значения HR были меньше 75% для 20 топографических единиц, из которых 13 ТЕ имели HR<50%. А из последних 1 ТЕ имела HR<25%.

4. Смоделированные зоны источников с наибольшей (>80%) вероятностью начала камнепада и части камнепадных полигонов из базы данных IFFI для уровня выше 90-го процентиля по высоте (верхних 90% высоты полигонов). Как и для комбинации 2, интерпретация сопоставления здесь менее очевидна, чем при любом значении ненулевой вероятности начала камнепада для закартированных зон источников, как в случае 3. Лишь 1 топографическая единица имела HR>20%, для 13 ТЕ оказалось, что HR<10%. А из последних 5 ТЕ имели HR<5%.

Результаты по определению подверженности железнодорожной сети Италии камнепадам с помощью модели STONE

Конечным результатом этой работы является классификация железнодорожной сети Италии, разделенной на сегменты длиной по 1 км, по подверженности камнепадам. Для этого наиболее важными являются шаги 1б–5б, перечисленные в подразделе «Моделирование траекторий камнепадов с помощью STONE». Авторы статьи [1] создали карты расчетных количеств траекторий на ячейку с использованием модели STONE. Затем были классифицированы все ячейки, охваченные выбранными склоновыми единицами (см. этап 2а в подразделе «Выявление зон источников камнепадов»), при этом использовалась карта для расчета уникального значения подверженности камнепадам каждого 1-километрового сегмента железной дороги.

Карта количеств траекторий на ячейку сетки, содержащая сильно различающиеся значения, была преобразована в карту относительных вероятностей в долях единицы (в интервале [0, 1]), то есть в карту подверженности камнепадам. Это было сделано с использованием эмпирических кумулятивных функций распределения (ECDF) количеств траекторий в пределах ячеек сетки, откалиброванных в подмножестве ячеек, в которых происходили камнепады, указанные в национальной базе данных IFFI (Trigila et al., 2010). Эта база включает полигоны, нанесенные на карту как «камнепадные» или как «обширные территории, содержащие камнепады». Авторы работы [1] рассчитали конкретные ECDF в каждой топографической единице, показанной на рисунке 1, а. На рисунке 4 показано несколько выборочных ECDF, соответствующих первым четырем топографическим единицам в таблицах 3, 4 и 5. Остальные ECDF очень похожи (их кривые накладываются на графики, представленные на рисунке 4).

На рисунке 8, б показано окончательное классифицированное количество траекторий (подверженность) в выбранном для примера месте. Эта растровая карта раскрашена в цвета от зеленого до красного, то есть соответственно от низких до высоких значений подверженности камнепадам. На рисунке 8, б карта подверженности сопоставляется с камнепадными полигонами из базы данных IFFI (см. также рис. 7) для этого места. Авторы статьи [1] выполнили валидацию классифицированных результатов, отраженных на карте подверженности, следующим образом. Были выбраны все камнепадные полигоны из базы данных IFFI в пределах буферных зон склоновых единиц, а затем выбрали ячейки сетки ЦМР внизу полигонов и попали в самый низкий по высоте 10-й процентиль, что также показано на рисунке 8. Авторы достаточно уверены в том, что эти ячейки в совокупности представляют собой зоны отложений камнепадного материала.

Сопоставление карт вероятности PQR для разных топографических единиц с зонами отложения полигонов из базы данных IFFI и с целыми полигонами из IFFI дало частоты совпадений HR, перечисленные в таблице 4.

Таблица 4. Частота совпадений модельной вероятности камнепадов P_QR с зонами транзита и отложения полигонов из базы данных IFFI

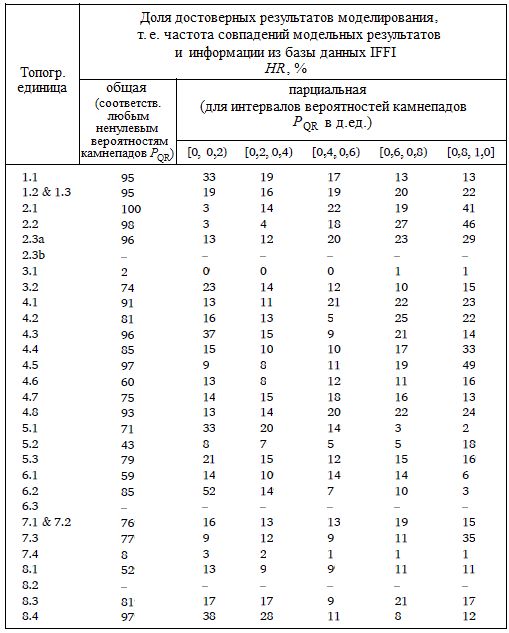
В таблице 5 перечислены результаты сравнения смоделированных зон источников камнепадов с целыми камнепадными полигонами из базы данных IFFI.

Отметим, что топографическая единица 2.3b не содержит зарегистрированных в IFFI камнепадов, имеющих отношение к железной дороге, а топографические единицы 6.3 и 8.2 не содержат пересечений железной дороги со склоновыми единицами, поэтому для этих трех зон значения HR в таблицах 4 и 5 не указаны (в оригинальной статье в таблице 5 по какой-то причине также нет значений HR для топографической единицы 7.4. – Ред.).

Таблица 5. Частота совпадений модельной вероятности камнепадов P_QR с целыми камнепадными полигонами из базы данных IFFI

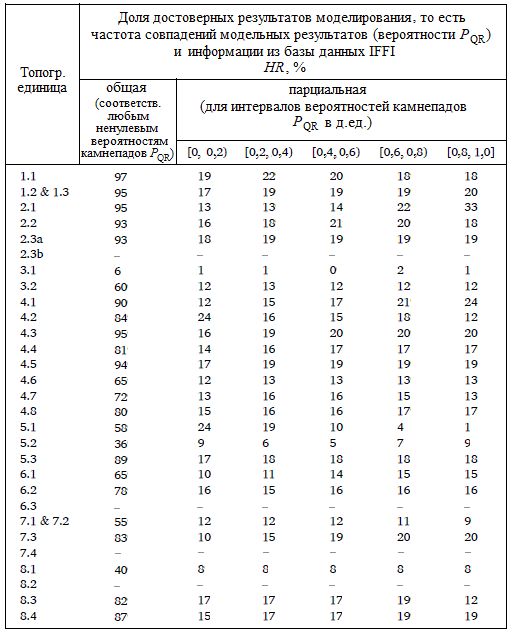
Следующим шагом была классификация железнодорожной сети, разделенной на 1-километровые сегменты. Для каждого сегмента, охватывающего множество значений вероятности камнепадов, выбиралась наибольшая величина. Это консервативный и разумный выбор, поскольку, если одна точка сегмента будет поражена камнепадом, то и весь сегмент будет непригоден для эксплуатации. С другой стороны, разбиение всего перегона, соединяющего два узла, на небольшие сегменты одинаковой длины гарантирует пространственную однородность. На рисунке 9, а показаны железнодорожные сегменты, классифицированные так, как указано выше. Общая длина железнодорожных трасс в Италии превышает 17 000 км, но в данной работе [1] не рассматривались участки, защищенные тоннелями, и участки за пределами цифровой модели рельефа TINITALY, но рассматривались участки, проходящие через равнинный рельеф. Таким образом, общая исследуемая длина железнодорожных трасс составила 16 084 км. Из них 14 724 км были отнесены к интервалу вероятности камнепадов [0, 0,2], 239 км – к [0,2, 0,4], 170 км – к [0,4, 0,6), 163 км – к [0,6, 0,8), 789 км – к [0,8, 1,0] (см. также таблицу 6).

К сожалению, имеющихся данных было недостаточно для валидации результатов классификации сегментов. Чтобы выполнить дополнительную оценку этих результатов, авторы работы [1] провели анализ графа и оценили значимость повреждений сегментов для работы всей железнодорожной сети.

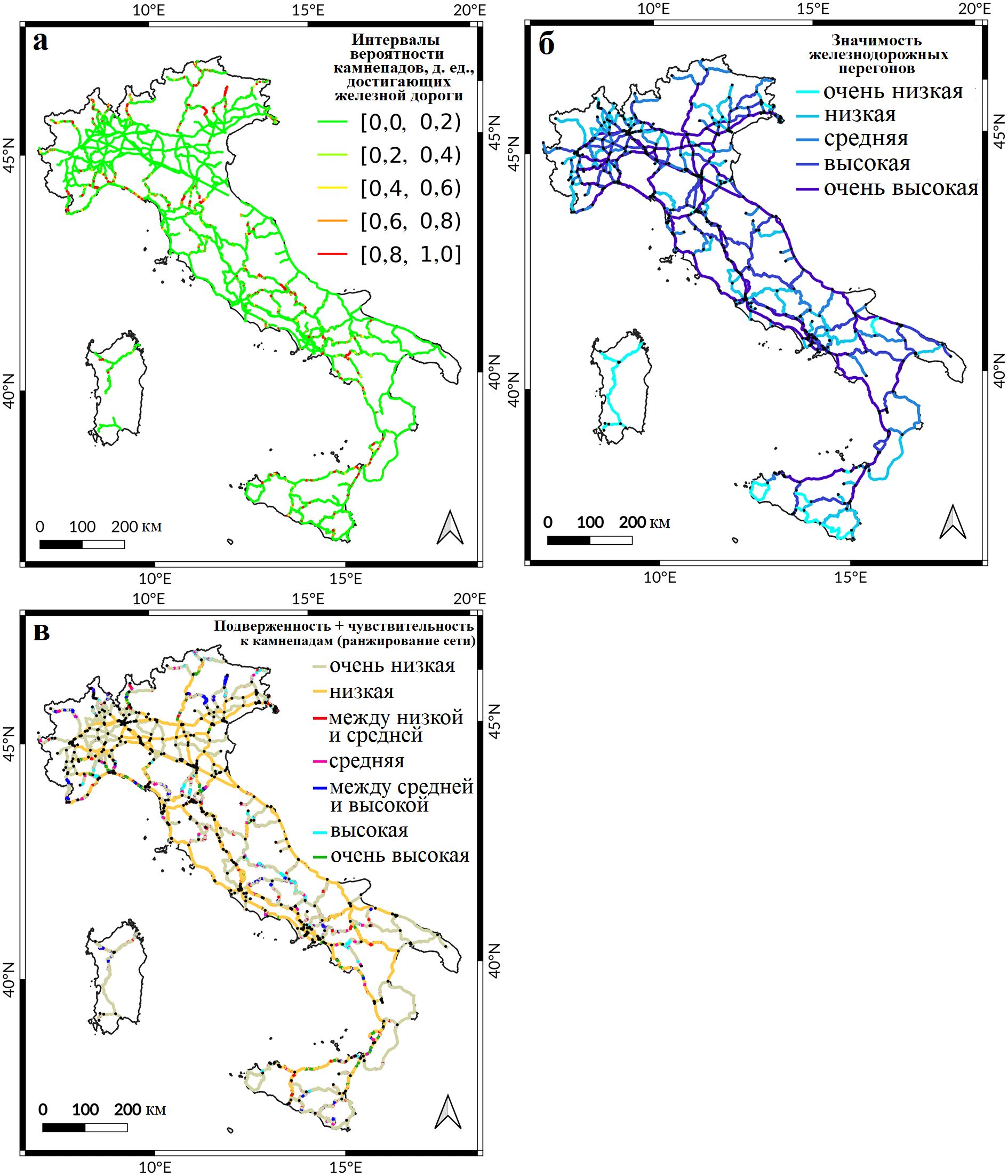
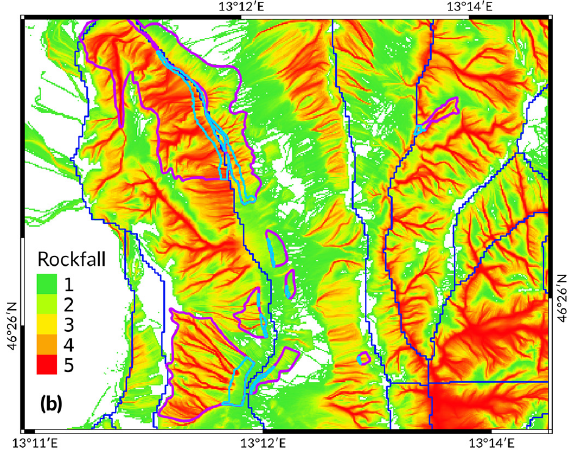
Рис. 9. Результаты работы: а – классификация итальянской железнодорожной сети, разделенной на 1-километровые сегменты, по вероятности камнепадов (подверженности сегментов камнепадам, смоделированной в STONE); б – значимость железнодорожных перегонов для итальянской железнодорожной сети, оцененная по центральности по промежуточности (степени посредничества), описанной в подразделе «Анализ железнодорожной сети в рамках теории графов» (см. рис. 5); в – ранжирование сети одновременно по подверженности камнепадам (их вероятности) и чувствительности к ним (значимости перегонов) (см. рис. 9, а, б и таблицу 6)

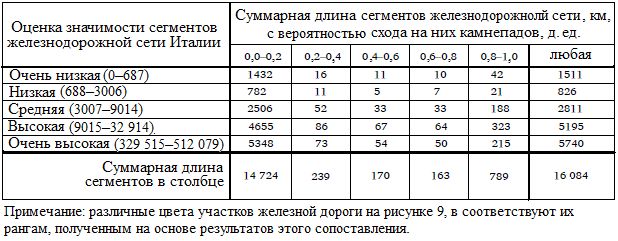
Таблица 6. Перекрестное сопоставление подверженности сегментов железных дорог Италии камнепадам и оценок их значимости для работы всей железнодорожной сети страны

Ранжирование железнодорожной сети по подверженности и чувствительности к камнепадам

В подразделе «Анализ железнодорожной сети в рамках теории графов» был определен новый показатель (атрибут) значимости каждого сегмента железной дороги, полученный как изменение общей центральности по промежуточности (степени посредничества) всех оставшихся ребер в сети, если ребро, соответствующее рассматриваемому сегменту, удалено из графа. На рисунке 9, б показаны результаты такого анализа при удалении ребер по одному. Четко видны наиболее значимые ребра с самыми темными оттенками синего цвета, и можно легко заметить разницу между результатами этого анализа и степенью посредничества, показанной на рисунке 5.

Классы, основанные на подверженности камнепадам железнодорожной сети, разделенной на 1-километровые сегменты, были определены в подразделе «Моделирование траекторий камнепадов с помощью STONE». Результаты этой классификации (5 классов) показаны на рисунке 9, а.

Изменение общей степени посредничества всех оставшихся ребер графа сети при удалении ребер по одному было определено в подразделе «Анализ железнодорожной сети в рамках теории графов» и в начале этого подраздела (см. рис. 9, б).

Это были промежуточные шаги на пути к последнему результату этой работы [1] – комбинированному ранжированию железнодорожной сети с учетом как классов сегментов по их подверженности камнепадам, так и классов сегментов по их значимости. Этот комбинированный анализ был выполнен самым простым из возможных способом – путем перекрестного рассмотрения двух указанных классификаций. Результаты такого ранжирования, выраженные в километрах железнодорожных трасс в каждом комбинированном классе, представлены в таблице 6. Всего получилось 25 классов (рангов). Но их для простоты изображения на карте разбили на 7 объединенных классов (класс с самой низкой подверженностью камнепадам, соответствующий наибольшей части железнодорожной сети, был разделен на два класса ранжированной чувствительности, а оставшаяся часть сети была почти равномерно разделена еще на пять классов). Результаты этого представлены на рисунке 9, в. Их сравнение с результатами классификации железнодорожной сети, основанной только на подверженности камнепадам (см. рис. 9, а), демонстрирует явные различия.

ВЫБОРОЧНОЕ ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ

Авторы статьи [1] подчеркивают, что национальную базу данных по оползням IFFI (Trigila et al., 2010; ISPRA, 2018) они использовали лишь для валидации результатов моделирования несколькими способами, но не применяли ее для построения или калибровки принятой в данной работе [1] модели камнепадов.

Выявление зон источников камнепадов

Иллюстрация сопоставления смоделированных вероятностей начала камнепадов в зонах источников, закартированных экспертами, и верхнего процентиля высотных отметок полигонов из базы данных IFFI представлена на рисунке 8 для одного конкретного района в топографической единице 1.2&1.3. Видно, что в этом районе ненулевые пиксели вероятностной карты источников охватывают бОльшие площади, чем было выявлено при экспертном картировании источников и чем было занято верхним процентилем высот полигонов из базы данных IFFI. Это обусловлено построением, поскольку статистическая процедура, описанная в подразделе «Выявление зон источников камнепадов», была разработана для консервативного присвоения ненулевых вероятностей любой ячейке сетки выше довольно низкого порога, основанного на величине наклона поверхности. Это согласуется с тем наблюдением, что зоны источников, нанесенные на карту экспертами, на самом деле имеют довольно низкие наклоны (см. рис. 3, 6). На рисунке 8, a показано хорошее соответствие вероятностной карты и верхних процентилей высот полигонов из базы данных IFFI, а также зон, закартированных экспертами, хотя не все эти зоны совпадают идеально.

Тем не менее степень соответствия модельных источников модели с закартированными зонами и полигонами из IFFI часто довольно низка (см. таблицу 3). Авторы работы [1] объясняют это следующими причинами. Чтобы построить модель зон источников, они приняли наличие взаимосвязи между вероятностью того, что ячейка сетки инициирует камнепад, и местным углом наклона поверхности. Это было компромиссом между приемлемым общим временем, необходимым для выполнения процедуры для большой исследуемой территории, и реалистичностью получаемых результатов. Но это, безусловно, не учитывало все свойства местного рельефа, которые влияют на экспертные критерии, применяемые для картирования зон потенциальных источников камнепадов. Более того, в процессе моделирования авторы делали конкретные выборы и допущения, часто произвольные.

Ошибки также могли возникать из-за несоответствия между цифровой моделью рельефа, использованной при анализе, и видимым разрешением изображений с сервиса Google Earth™, используемых для экспертного картирования, особенно для мест с самым крутым рельефом, которые больше всего интересовали авторов. При анализе они применяли ЦМР, сгенерированную на основе нерегулярной триангулировнной сети (ТНС), и визуальный осмотр карты с оттененным рельефом, созданной на основе выделенных на ЦМР мест, в которых проявляется триангуляция, использованная для подготовки ЦМР, что, несомненно, влияет на карту склонов по всей стране.

Модель STONE и подверженность камнепадам

Результатом моделирования в программе STONE является растровая карта, показывающая количества классифицированных траекторий на ячейку сетки. Для получения окончательных результатов своей работы авторы статьи [1] использовали эту карту несколькими способами:

1) сопоставили эту карту с информацией по камнепадным полигонам из базы данных IFFI;

2) разделили железнодорожную сеть на 1-километровые сегменты и классифицировали их на основе их подверженности камнепадам;

3) изучили свойства железнодорожной сети в рамках теории графов, рассматривая сеть в связи с ее чувствительностью к удалению ребер (аналогов перегонов между узлами) графа по одному, что помогло затем выполнить совместную классификацию по подверженности и чувствительности.

В таблицах 4 и 5 перечислены итоги валидации модельных результатов путем их сравнения соответственно с зонами транзита плюс отложения и с целыми камнепадными полигонами из базы данных IFFI. Значения общей доли  (частоты) совпадений HR в этом случае довольно велики, а это означает, что большинство зон транзита камнепадов в IFFI действительно перекрывались хотя бы с одной модельной траекторией камней.

Анализируя парциальные величины HR для разных интервалов модельной вероятности камнепадов в таблице 4, можно увидеть, что в большинстве случаев зоны транзита попадают в класс подверженности камнепадам в интервале их вероятности [0,8, 1,0], многие – в [0, 0,2), некоторые – в [0,4, 0,6) и [0,6, 0.,8) и ни одна – в [0,2, 0,4). Эта информация не требует однозначных выводов, хотя может быть интересна для дальнейшего использования, если будут усовершенствованы методы, представленные в этой работе. Скорее всего, указанные особенности могут быть связаны с процедурой выбора зон источников камнепадов (например, Rossi et al., 2021) или с использованием стратегии классификации по результатам подсчета траекторий.

В таблице 5 представлены итоги валидации модельных результатов путем их сравнения с целыми полигонами из базы данных IFFI в отличие от таблицы 4. Значения общей частоты совпадений HR довольно схожи со случаем, когда сравнение выполнялось с 10-м процентилем высоты каждого полигона, а в нескольких случаях и немного выше. Интересно, что здесь частоты совпадений почти всегда равномерно распределяются между пятью подклассами модельной вероятности камнепадов. Одной из причин этого может быть пространственная неточность выделенных полигонов из IFFI.

Модельный подсчет траекторий (см. рис. 8, б) дал растровую карту с разрешением 10 м. Но авторы считают конечным продуктом этой работы векторную карту железнодорожной сети, разбитую на сегменты длиной по 1 км, подразделенные на 5 классов по их подверженности камнепадам. Причина этого является двоякой. Во-первых, первоначальной целью авторов было создание карты, которую можно было бы использовать для ранжирования (приоритизации) мер безопасности на национальном уровне. Во-вторых, авторы принимали допущения и приближения, чтобы иметь возможность работать однородно в национальном масштабе; по этой причине растровая карта с разрешением 10 м может содержать локальные неточности, которые сглаживаются классификацией сегментов протяженностью по 1 км. Это подразумевает, что применение классифицированной карты предназначено для определения местоположений целых сегментов с наибольшей подверженностью камнепадам. Выводы для меньших (местных) масштабов все же могут быть получены в рамках модели STONE, но они должны потверждаться данными с более высоким разрешением.

Совместная классификация железнодорожной сети по подверженности камнепадам и по чувствительности к выходу из строя отдельных перегонов

Объединенное ранжирование железнодорожной сети Италии по подверженности и чувствительности к камнепадам было выполнено на основе перекрестной комбинации пяти классов сегментов по вероятности схода на них камнепадов и пяти классов перегонов по их значимости для функционирования всей сети (см. таблицу 6 и рис 9, в).

Как уже было отмечено, в этом случае были получены несколько необычные результаты (см. рис 9, в): сегменты с незначительной подверженностью камнепадам (см. рис. 9, а) не попадали в низший ранг по чувствительности сети к их выходу из строя. Но следует отметить, что из 25 комбинаций из таблицы 6 было почти произвольно выделено 7 комбинированных классов, представленных на рисунке 9, в, – отсюда и некоторые несоответствия.

Авторы статьи [1] рассматривают указанную комбинированную классификацию просто как методологическое предложение. Они не пытались здесь оптимизировать конечные классы на более высоком уровне, хотя это можно было бы выполнить с подходящими точными данными для валидации – по наблюденным камнепадам и (возможно) по пересечению ими железнодорожных путей, а также по фактической работе всей сети.

Знание фактического железнодорожного трафика подразумевает свойства сети. На самом деле в этой работе [1] степень посредничества узлов и ребер рассчитывалась с учетом кратчайших путей между всеми возможными парами. Если бы авторы статьи [1] заменили их реальными маршрутами, они бы получили другую сеть и другой соответствующий граф (Kurant, Thiran, 2006). Вот еще один пример. Знание количества поездов, проходящих в день по каждому железнодорожному перегону, можно было бы использовать для определения значимости ребер другим способом, а не на основе простой топологии сети, рассмотренной здесь. Аналогичным образом могла бы помочь дополнительная информация о среднем количестве пассажиров на перегон в день. С другой стороны, информация о присутствии поездов в реальном времени на каждом перегоне сети хотя и не является сложной для рассмотрения с технической точки зрения, но не имеет непосредственного отношения к выполненной работе [1]. Получение такой информации потребовало бы включения некоего динамического механизма фактического отрыва каменного материала выше по склону над каждым железнодорожным перегоном, а также мониторинга возможных инициирующих камнепады событий в реальном времени.

ВЫВОДЫ

В данной работе [1] был выполнен физически обоснованный анализ подверженности камнепадам итальянской железнодорожной сети на площади 25 400 км². Выборка источников камнепадов, нанесенная на карту экспертами, помогла разработать вероятностную идентификацию потенциальных источников на основе цифровой модели рельефа и углов наклона поверхности. Расположение источников было ключевым исходным материалом для трехмерного моделирования зон транзита камнепадов из любого возможного источника в программе STONE. Сегменты железнодорожной сети были разделены на классы по подверженности камнепадам и на классы по их значимости для работы всей сети. В результате была разработана совместная классификация на основе предыдущих двух.

Чтобы справиться с проблемами, связанными с большими размерами изучаемой территории, обширными картографическими и вычислительными трудностями, обязательно принимались допущения и приближения. Дополнительным моментом здесь является то, что из-за больших размеров исследуемой территории и отсутствия конкретных данных камнепады на застроенных склонах не рассматривались. При этом достоинством этой работы является предложение эффективной процедуры оценки подверженности и чувствительности к камнепадам железных дорог на очень большой и геоморфологически разнообразной исследуемой территории.

На основе выполненной работы были сделаны следующие выводы.

1. Процедура определения зон источников камнепадов основывалась на статистическом обобщении распределения углов наклона в пределах камнепадных полигонов, нанесенных на карту экспертами. Результаты валидации путем анализа частоты (доли) совпадений HR с информацией по камнепадам из базы данных IFFI показали, что указанная процедура в принципе пригодна для идентификации источников на больших территориях (в данной работе исследуемая площадь составляла около 25 000 км²), хотя улучшение качества калибровки потребовало бы включения дополнительных морфометрических переменных помимо наклона поверхности.

2. Траектории камнепадов моделировались с помощью программы STONE. Результаты валидации классифицированных зон транзита с точки зрения частоты совпадений HR с информацией по камнепадам из базы данных IFFI были достаточно удовлетворительными, поскольку большинство значений HR относилось к верхнему квартилю распределения вероятностей. Далее авторы статьи [1] совместили карту подверженности камнепадам территории страны и карту железнодорожной сети, разбили железные дороги на сегменты длиной по 1 км и подразделили эти сегменты на классы подверженности камнепадам. Более надежная валидация величин подверженности требует дополнительных данных.

3. При анализе возможного воздействия камнепадов на железнодорожную сеть Италии поочередно учитывалось влияние выхода из строя одного перегона на функционирование всей сети. Таким образом было выполнено ранжирование перегонов по их значимости для сети (в рамках теории графов). Затем была выполнена комбинированная классификация сети с учетом как подверженности, так и чувствительности к камнепадам. Авторы статьи [1] расценивают этот шаг как методологическое предложение, оптимизация и валидация которого потребуют специальных данных и дополнительных знаний о фактическом железнодорожном трафике в сети.

Следует подчеркнуть, что в данной работе информация из национальной базы данных по оползням IFFI (Trigila et al., 2010) помогла подтвердить приемлемую достоверность результатов моделирования, но не использовалась ни при идентификации источников камнепадов, которая требовала экспертного картирования, ни при моделировании зон транзита каменного материала. Это оставляет возможность для усовершенствования процедуры, поскольку авторы статьи [1] для характеристики закартированных экспертами полигонов использовали только распределение углов наклона поверхности. То есть оба шага (идентификация источников камнепадов и моделирование их транзита), в принципе, могут быть расширены.

Следует также отметить, что естественной эволюцией выполненного здесь анализа топологических свойств железнодорожной сети является мониторинг сети в реальном времени (поначалу еще статический, без учета трафика) в зависимости от развития в реальном времени возможных инициирующих событий. Собственно, это и было первоначальным мотивом этой работы. Представленная здесь карта подверженности сегментов железной дороги камнепадам вместе с аналогичной картой их подверженности обломочным потокам, селям и оползням дисперсных грунтов были ключевыми входными данными для прототипа системы раннего предупреждения, создание которого финансировалось Национальной железнодорожной компанией (RFI) в рамках реализации Национальной системы раннего предупреждения об оползнях, вызванных дождями (SANF) (Rossi et al., 2012; Guzzetti et al., 2020).

-

Эта работа была частично поддержана владельцем железнодорожной сети Италии Rete Ferroviaria Italiana (RFI) – дочерней компанией государственного холдинга Ferrovie dello Stato (FS).

Перевод статьи на русский язык подготовлен редакцией при поддержке компании «ГАБИОНЫ МАККАФЕРРИ СНГ» – партнера и одного из генеральных спонсоров журнала «ГеоИнфо».

ИСТОЧНИК ДЛЯ ПЕРЕВОДА

1. Alvioli M., Santangelo M., Fiorucci F., Cardinali M., Marchesini I., Reichenbach P., Rossi M., Guzzetti F., Peruccacci S. Rockfall susceptibility and network-ranked susceptibility along the Italian railway // Engineering Geology. Vol. 293. Elsevier B.V., November 2021. P. 106301. URL: doi.org/10.1016/j.enggeo.2021.106301.

SOURCE FOR THE TRANSLATION

1. Alvioli M., Santangelo M., Fiorucci F., Cardinali M., Marchesini I., Reichenbach P., Rossi M., Guzzetti F., Peruccacci S. Rockfall susceptibility and network-ranked susceptibility along the Italian railway. Engineering Geology. Elsevier B.V., 2021, 293: 106301. URL: doi.org/10.1016/j.enggeo.2021.106301.

СПИСОК ЛИТЕРАТУРЫ [REFERENCES]

Agliardi, F., Crosta, G.B., 2003. High resolution three-dimensional numerical modelling of rockfalls. Int. J. Rock Mech. Min. Sci. 40, 455–471. https://doi.org/10.1016/ S1365-1609(03)00021-2.

Albert, R., Jeong, H., Barabasi, A.L., 2000. Error and attack tolerance of complex networks. Nature 406, 378–382. https://doi.org/10.1038/35019019.

Alvioli, M., 2020. Administrative boundaries and urban areas in Italy: A perspective from scaling laws. Landsc. Urban Plan. 204, 103906. https://doi.org/10.1016/j. landurbplan.2020.103906.

Alvioli, M., Marchesini, I., Reichenbach, P., Rossi, M., Ardizzone, F., Fiorucci, F., Guzzetti, F., 2016. Automatic delineation of geomorphological slope units with r. slopeunits v1.0 and their optimization for landslide susceptibility modeling. Geosci. Model Dev. 9, 3975–3991. https://doi.org/10.5194/gmd-9-3975-2016.

Alvioli, M., Guzzetti, F., Marchesini, I., 2020a. Parameter-free delineation of slope units and terrain subdivision of Italy. Geomorphology 358, 107124. https://doi.org/ 10.1016/j.geomorph.2020.107124.

Alvioli, M., Santangelo, M., Fiorucci, F., Cardinali, M., Marchesini, I., Reichenbach, P., Rossi, M., 2020b. A data-driven method for assessing the probability for terrain grid cells of initiating rockfalls on a large area. In: Alvioli, M., Marchesini, I., Melelli, L., Guth, P. (Eds.), Proceedings of the sixth Geomorphometry conference: Geomorphometry 2020, CNR Edizioni, Rome, Perugia, Italy. https://doi.org/ 10.30437/geomorphometry2020_43.

Amato, G., Fiorucci, M., Martino, S., Lombardo, L., Palombi, L., 2020. Earthquake–Triggered Landslide Susceptibility in Italy by Means of Artificial Neural Network. https://doi.org/10.31223/X59W39.

Barthelemy, M., 2011. Spatial networks. Phys. Rep. 499, 1–101. https://doi.org/ 10.1016/j.physrep.2010.11.002.

Bassolas, A., Gallotti, R., Lamanna, F., Lenormand, M., Ramasco, J.J., 2020. Scaling in the recovery of urban transportation systems from massive events. Sci. Rep. 10, 2746. https://doi.org/10.1038/s41598-020-59576-1.

Battaglini, L., Campo, V., Cipolloni, C., Congi, M.P., Delogu, D., Ventura, R., 2012. Carta geologica d’Italia alla scala 1:100,000. WWW site. ISPRA. Via Vitaliano Brancati, 48 — 00144 Rome, Italy. URL. http://193.206.192.231/carta_geologica_italia/cartageologica. htm.

Bornaetxea, T., Rossi, M., Marchesini, I., Alvioli, M., 2018. Effective surveyed area and its role in statistical landslide susceptibility assessments. Nat. Hazards Earth Syst. Sci. 18, 2455–2469. https://doi.org/10.5194/nhess-18-2455-2018.

Bourrier, F., Dorren, L., Hungr, O., 2013. The use of ballistic trajectory and granular flow models in predicting rockfall propagation. Earth Surf. Process. Landf. 38, 435–440. https://doi.org/10.1002/esp.3372.

Bucci, F., Santangelo, M., Fongo, L., Marchesini, I., Alvioli, M., Cardinali, M., Melelli, L., 2021. A new lithological Map of Italy at 1:100,000 Scale for geo-mechanical modeling. In preparation.

Buyer, A., Aichinger, S., Schubert, W., 2020. Applying photogrammetry and semi-automated joint mapping for rock mass characterization. Eng. Geol. 264, 105332. https://doi.org/10.1016/j.enggeo.2019.105332.

Camilo, D.C., Lombardo, L., Mai, P.M., Dou, J., Huser, R., 2017. Handling high predictor dimensionality in slope-unit-based landslide susceptibility models through lasso-penalized generalized linear model. Environ. Model. Softw. 97, 145–156. https:// doi.org/10.1016/j.envsoft.2017.08.003.

Casagrande, L., Cavallini, P., Frigeri, A., Furieri, A., Marchesini, I., Neteler, M., 2007. GIS Open Source. Flaccovio, Palermo (In Italian).

Cats, O., Yap, M., van Oort, N., 2016. Exposing the role of exposure: Public transport network risk analysis. Transp. Res. A Policy Pract. 88, 1–14. https://doi.org/ 10.1016/j.tra.2016.03.015.

Chartrand, G., Chartrand, G., Lesniak, L., Lesniak, L., Zhang, P., 1993. Graphs & Digraphs. Chapman and Hall/CRC, Boca Raton, FL.

Chen, Z., Liang, S., Ke, Y., Yang, Z., Zhao, H., 2020. Landslide susceptibility assessment using different slope units based on the evidential belief function model. Geocarto Int. 35, 1641–1664. https://doi.org/10.1080/10106049.2019.1582716.

Cohen, R., Erez, K., Ben Avraham, D., Havlin, S., 2000. Resilience of the internet to random breakdowns. Phys. Rev. Lett. 85, 4626–4628. https://doi.org/10.1103/ PhysRevLett.85.4626.

Collins, B.D., Stock, G.M., 2016. Rockfall triggering by cyclic thermal stressing of exfoliation fractures. Nat. Geosci. 9, 395–400. https://doi.org/10.1038/ngeo2686.

Corominas, J., Mavrouli, O., Ruiz-Carulla, R., 2018. Magnitude and frequency relations: are there geological constraints to the rockfall size? Landslides 15, 829–845. https:// doi.org/10.1007/s10346-017-0910-z.

Delonca, A., Gunzburger, Y., Verdel, T., 2014. Statistical correlation between meteorological and rockfall databases. Nat. Hazards Earth Syst. Sci. 14, 1953–1964. https://doi.org/10.5194/nhess-14-1953-2014.

Evans, S.G., Hungr, O., 1993. The assessment of rockfall hazard at the base of talus slopes. Can. Geotech. J. 30, 620–636. https://doi.org/10.1139/t93-054.

Fongo, L., 2018. Verso una nuova carta litologica d’Italia in scala 1:100,000 (in Italian) Master Thesis. University of Perugia.

Frattini, P., Crosta, G., Carrara, A., Agliardi, F., 2008. Assessment of rockfall susceptibility by integrating statistical and physically–based approaches. Geomorphology 94, 419–437. https://doi.org/10.1016/j.geomorph.2006.10.037. GIS technology and models for assessing landslide hazard and risk.

Freeman, L.C., 1978. Centrality in social networks conceptual clarification. Soc. Networks 1, 215–239. https://doi.org/10.1016/0378-8733(78)90021-7.

Giordan, D., Adams, M.S., Aicardi, I., Alicandro, M., Allasia, P., Baldo, M., Berardinis, P. D., Dominici, D., Godone, D., Hobbs, P., Lechner, V., Niedzielski, T., Piras, M., Rotilio, M., Salvini, R., Segor, V., Sotier, B., Troilo, F., 2020. The use of unmanned aerial vehicles (uavs) for engineering geology applications. Bull. Eng. Geol. Environ. 79, 3437–3481. https://doi.org/10.1007/s10064-020-01766-2.

Guzzetti, F., Reichenbach, P., 1994. Towards a definition of topographic divisions for Italy. Geomorphology 11, 57–74. https://doi.org/10.1016/0169-555X(94)90042-6.

Guzzetti, F., Crosta, G., Detti, R., Agliardi, F., 2002. STONE: a computer program for the three-dimensional simulation of rock-falls. Comput. Geosci. 28, 1079–1093. https:// doi.org/10.1016/S0098-3004(02)00025-0.

Guzzetti, F., Reichenbach, P., Wieczorek, G.F., 2003. Rockfall hazard and risk assessment in the Yosemite Valley, California, USA. Nat. Hazards Earth Syst. Sci. 3, 491–503. https://doi.org/10.5194/nhess-3-491-2003.

Guzzetti, F., Reichenbach, P., Ghigi, S., 2004. Rockfall hazard and risk assessment along a transportation corridor in the Nera Valley, Central Italy. Environ. Manag. 34, 191–208. https://doi.org/10.1007/s00267-003-0021-6.

Guzzetti, F., Gariano, S.L., Peruccacci, S., Brunetti, M.T., Marchesini, I., Rossi, M., Melillo, M., 2020. Geographical landslide early warning systems. Earth Sci. Rev. 200, 102973. https://doi.org/10.1016/j.earscirev.2019.102973.

Hungr, O., Evans, S.G., Hazzard, J., 1999. Magnitude and frequency of rock falls and rock slides along the main transportation corridors of southwestern British Columbia. Can. Geotech. J. 36, 224–238. https://doi.org/10.1139/t98-106.

ISPRA, 2018. Landslides and floods in Italy: hazard and risk indicators — Summary Report 2018. Technical report. The Institute for Environmental Protection and Research, Via Vitaliano Brancati, 48 — 00144 Rome, Italy. URL. http://www. isprambiente.gov.it.287/bis/2018.

Jaboyedoff, M., Oppikofer, T., Abellan, A., Derron, M.H., Loye, A., Metzger, R., Pedrazzini, A., 2012. Use of LIDAR in landslide investigations: a review. Nat. Hazards 61, 5–28. https://doi.org/10.1007/s11069-010-9634-2.

Jacobs, L., Kervyn, M., Reichenbach, P., Rossi, M., Marchesini, I., Alvioli, M., Dewitte, O., 2020. Regional susceptibility assessments with heterogeneous landslide information: Slope unit- vs. pixel-based approach. Geomorphology 356, 107084. https://doi.org/ 10.1016/j.geomorph.2020.107084.

Katifori, E., Szollosi, G.J., Magnasco, M.O., 2010. Damage and fluctuations induce loops in optimal transport networks. Phys. Rev. Lett. 104, 048704 https://doi.org/ 10.1103/PhysRevLett.104.048704.

Kurant, M., Thiran, P., 2006. Extraction and analysis of traffic and topologies of transportation networks. Phys. Rev. E 74 (3), 036114. https://doi.org/10.1103/ PhysRevE.74.036114.

Li, L., Lan, H., 2020. Integration of spatial probability and size in slope-unit-based landslide susceptibility assessment: A case study. Int. J. Environ. Res. Public Health 17, 8055. https://doi.org/10.3390/ijerph17218055.

Li, H., Li, X., Li, W., Zhang, S., Zhou, J., 2019. Quantitative assessment for the rockfall hazard in a post–earthquake high rock slope using terrestrial laser scanning. Eng. Geol. 248, 1–13. https://doi.org/10.1016/j.enggeo.2018.11.003.

Lu, L., Zhang, M., 2013. Edge betweenness centrality. In: Dubitzky, W., Wolkenhauer, O., Cho, K.H., Yokota, H. (Eds.), Encyclopedia of Systems Biology. Springer New York, New York, NY, pp. 647–648. https://doi.org/10.1007/978-1-4419-9863-7_874.

Macciotta, R., Martin, C.D., Edwards, T., Cruden, D.M., Keegan, T., 2015. Quantifying weather conditions for rock fall hazard management. Georisk 9, 171–186. https:// doi.org/10.1080/17499518.2015.1061673.

Marchesini, I., Rossi, M., Alvioli, M., Santangelo, M., Cardinali, M., 2020. Slope–catchment area relationship for debris-flow source area identification. In: Alvioli, M., Marchesini, I., Melelli, L., Guth, P. (Eds.), Proceedings of the sixth Geomorphometry conference: Geomorphometry 2020, CNR Edizioni, Rome, Perugia, Italy. https://doi.org/10.30437/geomorphometry2020_47.

Matas, G., Lantada, N., Corominas, J., Gili, J., Ruiz-Carulla, R., Prades, A., 2017. Simulation of full–scale rockfall tests with a fragmentation model. Landslides 14, 1565–1578. https://doi.org/10.1007/s10346-017-0818-7.

Matas, G., Lantada, N., Corominas, J., Gili, J., Ruiz-Carulla, R., Prades, A., 2020. Simulation of full–scale rockfall tests with a fragmentation model. Geosciences 10, 168. https://doi.org/10.3390/geosciences10050168.

Matasci, B., Stock, G.M., Jaboyedoff, M., Carrea, D., Collins, B.D., Guerin, A., Matasci, G., Ravanel, L., 2018. Assessing rockfall susceptibility in steep and overhanging slopes using three-dimensional analysis of failure mechanisms. Landslides 15, 859–878. https://doi.org/10.1007/s10346-017-0911-y.

Mattsson, L.G., Jenelius, E., 2015. Vulnerability and resilience of transport systems -— a discussion of recent research. Transp. Res. A Policy Pract. 81, 16–34. https://doi. org/10.1016/j.tra.2015.06.002. Resilience of Networks.

Mavrouli, O., Corominas, J., 2020. Evaluation of maximum rockfall dimensions based on probabilistic assessment of the penetration of the sliding planes into the slope. Rock Mech. Rock. Eng. 53, 2301–2312. https://doi.org/10.1007/s00603-020-02060-z.

Melillo, M., Gariano, S., Peruccacci, S., Sarro, R., Mateos, R.M., Brunetti, M.T., 2020. Rainfall and rockfalls in the Canary Islands: assessing a seasonal link. Nat. Hazards Earth Syst. Sci. 20, 2307–2317. https://doi.org/10.5194/nhess-20-2307-2020.

Melzner, S., Rossi, M., Guzzetti, F., 2020. Impact of mapping strategies on rockfall frequency-size distributions. Eng. Geol. 272, 105639. https://doi.org/10.1016/j. enggeo.2020.105639.

Menegoni, N., Giordan, D., Perotti, C., 2021. An open-source algorithm for 3d rock slope kinematic analysis (roka). Appl. Sci. 11 https://doi.org/10.3390/app11041698.

Neteler, M., Mitasova, H., 2007. Open Source GIS: A GRASS GIS Approach. Springer, New York.

Perez-Rey, I., Riquelme, A., Gonzalez-de-Santos, L.M., Estevez-Ventosa, X., Tomas, R., Alejano, L.R., 2019. A multi–approach rockfall hazard assessment on a weathered granite natural rock slope. Landslides 16, 2005–2015. https://doi.org/10.1007/ s10346-019-01208-5.

Riquelme, A.J., Abellan, A., Tomas, R., Jaboyedoff, M., 2014. A new approach for semi-automatic rock mass joints recognition from 3D point clouds. Comput. Geosci. 68, 38–52. https://doi.org/10.1016/j.cageo.2014.03.014.

Rossi, M., Peruccacci, S., Brunetti, M.T., Marchesini, I., Luciani, S., Ardizzone, F., Balducci, V., Bianchi, C., Cardinali, M., Fiorucci, F., Mondini, A.C., Reichenbach, P., Salvati, P., Santangelo, M., Bartolini, D., Gariano, S.L., Palladino, M., Vessia, G., Viero, A., Andronico, L., Borselli, L., Deganutti, A.M., Iovine, G., Luino, F., Parise, M., Polemio, M., Guzzetti, F., Tonelli, G., 2012. SANF: National warning system for rainfall-induced landslides in Italy. In: Proceedings 11th Symposium on Landslides and 2nd north American Symposium on Landslides, Banff, Canada, pp. 1895–1899.

Rossi, M., Sarro, R., Reichenbach, P., Mateos, R.M., 2021. Probabilistic identification of rockfall source areas at regional scale in El Hierro (Canary Islands, Spain). Geomorphology 381, 107661. https://doi.org/10.1016/j.geomorph.2021.107661.

Ruiz-Carulla, R., Corominas, J., Gili, J.A., Matas, G., Lantada, N., Moya, J., Prades, A., Nunez Andres, M.A., Buill, F., Puig, C., 2020. Analysis of fragmentation of rock blocks from real–scale tests. Geosciences 10, 308. https://doi.org/10.3390/ geosciences10080308.

Santangelo, M., Alvioli, M., Baldo, M., Cardinali, M., Giordan, D., Guzzetti, F., Marchesini, I., Reichenbach, P., 2019. Brief communication: Remotely piloted aircraft systems for rapid emergency response: road exposure to rockfall in Villanova di Accumoli (Central Italy). Nat. Hazards Earth Syst. Sci. 19, 325–335. https://doi. org/10.5194/nhess-19-325-2019.

Santangelo, M., Marchesini, I., Bucci, F., Cardinali, M., Cavalli, M., Crema, S., Marchi, L., Alvioli, M., Guzzetti, F., 2020. Exposure to landslides in rural areas in Central Italy. J. Maps 0, 1–9. https://doi.org/10.1080/17445647.2020.1746699.

Sarro, R., Mateos, R.M., Reichenbach, P., Aguilera, H., Riquelme, A., Hernandez- Gutierrez, L.E., Martin, A., Barra, A., Solari, L., Monserrat, O., Alvioli, M., Fernandez- Merodo, J.A., Lopez-Vinielles, J., Herrera, G., 2020. Geotechnics for rockfall assessment in the volcanic island of Gran Canaria (Canary Islands, Spain). J. Maps 16, 605–613. https://doi.org/10.1080/17445647.2020.1806125.

Schlogel, R., Marchesini, I., Alvioli, M., Reichenbach, P., Rossi, M., Malet, J.P., 2018. Optimizing landslide susceptibility zonation: Effects of DEM spatial resolution and slope unit delineation on logistic regression models. Geomorphology 301, 10–20. https://doi.org/10.1016/j.geomorph.2017.10.018.

Tacchia, D., 2004. Cartografia ufficiale geologica e geomorfologica. Technical report. ISPRA. Via Vitaliano Brancati, 48 — 00144 Rome, Italy. URL. http://sgi. isprambiente.it/geologia100k/Documenti/cartuffgeo.pdf.

Tanyas, H., Rossi, M., Alvioli, M., van Westen, C.J., Marchesini, I., 2019a. A global slope unit-based method for the near real-time prediction of earthquake-induced landslides. Geomorphology 327, 126–146. https://doi.org/10.1016/j. geomorph.2018.10.022.

Tanyas, H., van Westen, C.J., Persello, C., Alvioli, M., 2019b. Rapid prediction of the magnitude scale of landslide events triggered by an earthquake. Landslides 16, 661–676. https://doi.org/10.1007/s10346-019-01136-4.

Tarquini, S., Isola, I., Favalli, M., Mazzarini, F., Bisson, M., Pareschi, M.T., Boschi, E., 2007. TINITALY/01: a new Triangular Irregular Network of Italy. Ann. Geophys. 50, 407–425. https://doi.org/10.4401/ag-4424.

Trigila, A., Iadanza, C., Spizzichino, D., 2010. Quality assessment of the Italian Landslide Inventory using GIS processing. Landslides 7, 455–470. https://doi.org/10.1007/ s10346-010-0213-0.

Turanboy, A., Ulker, E., Cuksutcu, C.B.K., 2018. A new approach for assessing stability of rock slopes considering centroids of weak zones. J. Min. Environ. 9, 1–18. https:// doi.org/10.22044/jme.2017.5975.1414.