Простой эмпирический метод устранения эффектов рефракции при фотограмметрии мелководья на основе съемки с БПЛА

ВВЕДЕНИЕ

Измерение топографических данных речных берегов и дна играет важную роль в различных управленческих и исследовательских работах, таких как определение гидроморфологических особенностей рек [2], изучение деформаций русла и береговой эрозии [3], оценка качества местообитаний речных организмов [4] и т. д. Такие данные обычно получают путем обычной полевой съемки, основанной на поперечных профилях в местах, выбранных для фиксации характерных особенностей рельефа [5]. Однако большинство методов полевой съемки требуют значительных затрат труда и средств, а пространственное и временное разрешение их результатов ограниченны.

Для повышения надежности различных операций необходима более частая и плотная съемка. Аэрофотограмметрия по стереоизображениям основана на методе съемки с широким полем зрения. До сих пор она использовалась для обеспечения топографического моделирования с хорошим пространственным разрешением на основе создания облака точек высокой плотности. Однако применение этого метода является ограниченным, поскольку для обработки получаемых с его помощью данных требуется дорогостоящее оборудование (например, летательный аппарат и датчик) и специальные знания пользователей.

В последние годы разработка процедуры SfM-MVS (то есть метода автоматической обработки изображений с определением структуры объекта по отображению движения (Structure-from-Motion, SfM) вкупе с получением стереоизображений по многовидовым изображениям (Multi-View Stereo, MVS)) предоставила возможность недорогого сбора трехмерных данных. Этот способ автоматической обработки изображений значительно снижает уровень знаний и умений, необходимых для извлечения пространственных данных высокого разрешения и высокой точности с использованием дешевых цифровых камер потребительского класса, установленных на беспилотных летательных аппаратах (БПЛА, дронах). Мониторинг как открытой, так и затопленной поверхности грунта в руслах рек с использованием процедуры SfM-MVS становится все более востребованным для создания высокоточных карт местности. Ее пригодность для открытой поверхности уже доказана: она дает результаты высокой точности для сухих участков [6]. Однако, как показали исследования с использованием цифровой фотограмметрии [6–8], для затопленной поверхности грунта точность цифровой модели рельефа (ЦМР), получаемой с помощью SfM-MVS, несколько ниже из-за преломления света на границе раздела «воздух – вода». Из-за этого на затопленных территориях зафиксированная глубина воды получается меньше реальной. Поэтому при построении ЦМР дна в таких случаях требуется внесение поправок на рефракцию (преломление).

При использовании одного из ранее разработанных методов такой коррекции [9] для преобразования кажущейся глубины воды в реальную в качестве поправочного коэффициента (CF – correction factor) используется показатель преломления воды, равный 1,34. Это минимально возможное значение, которое можно использовать, когда эффект преломления очень низок (то есть когда главная оптическая ось фотокамеры направлена вертикально вниз («в надир») на горизонтальную поверхность.

Геометрически можно показать, что такой поправочный коэффициент не всегда является оптимальным, как было доказано в случае двух камер в статье [10]. Согласно этой работе [10] величина CF изменяется в зависимости от положений этих двух камер относительно целевых точек. Однако при реальной подводной фотограмметрии расчет геометрического поправочного коэффициента не представляется возможным по двум причинам:

1) ни один исследователь не вывел геометрический CF для случаев с более чем двумя изображениями;

2) обычные программы для фотограмметрии не выдают информацию о том, какая камера использовалась для оценки координат каждой точки (в плотном облаке точек), что необходимо для расчета геометрического CF.

В настоящей статье представлен новый эмпирический метод, который разумно определяет поправочный коэффициент для конкретного полета БПЛА путем минимизации среднеквадратической ошибки для скорректированных высотных отметок дна. Также описывается проверка его эффективности при использовании для двух речных участков. Полученные значения среднеквадратических и средних ошибок для скорректированных высотных отметок дна сравнивались с их величинами, полученными с применением трех существующих методов: метода без коррекции (CF=1); обычного метода с использованием CF=1,34; метода с использованием эмпирической линейной регрессионной зависимости между измеренной и оцененной глубиной воды [11].

МЕТОД ИССЛЕДОВАНИЙ

Место исследований

В данной работе были исследованы два участка (1 и 2) в пределах главной части реки Саба в японской префектуре Ямагути. Первый располагался примерно в 8,5 км от устья этой реки, а второй – примерно в 1,7 км выше по течению от первого (рис. 1).

Рис. 1. Исследованные участки 1 (а) и 2 (б) на реке Саба и расположение на них точек, высотные отметки которых были измерены с помощью глобальной навигационной спутниковой системы (GPS) в режиме реального времени (RTK) (по [1])

Получение и выбор изображений

Аэрофотоснимки были получены с помощью цифровой камеры 4K, прикрепленной к небольшому легкому (1,28 кг) квадрокоптеру DJI Phantom 3 Professional. Этот БПЛА летел на высоте 25–30 м над поверхностью земли, чтобы получить изображения обоих участков с пространственным разрешением примерно 1 см. Каждое полученное изображение охватывало площадь около 64 м x 48 м. Снимки делались с большими перекрытиями (более 80%), чтобы обеспечить последующий подбор изображений во время обработки SfM (с определением структуры объекта по отображению движения). Общее количество изображений, собранных на участках 1 и 2, составило 240 и 424 соответственно. Во время каждой полевой съемки положение камеры устанавливалось практически «в надир» (вертикально вниз, то есть велась плановая аэрофотосъемка), чтобы уменьшить нежелательные эффекты отражений от поверхности воды на полученных изображениях. В конце все изображения были проверены и было удалено несколько снимков с эффектами «размытия».

Измерения методом RTK-GPS

Были выполнены измерения с помощью глобальной навигационной спутниковой системы (GPS) в режиме реального времени (RTK) для точек как на открытой, так и на затопленной поверхности грунта (см. рис. 1). Точки на открытой поверхности были разного рода наземными ориентирами, узнаваемыми на аэрофотоснимках, – опознаками (метками), которые были установлены заранее. Они были распределены таким образом, чтобы как можно лучше охватить весь изучаемый участок (например, на участке 1 – на обоих берегах реки и на мосту). Некоторые из опознаков использовались в качестве наземных контрольных точек (НКТ) с известными пространственными координатами для использования при обработке данных с помощью процедуры SfM-MVS, а некоторые – для валидации самого метода SfM-MVS.

Подводные точки были двух типов:

1) 10 черно-белых меток (марок), которые использовались только на участке 2;

2) точки, распределенные так, чтобы охватить различные глубины и типы дна реки.

Создание карты кажущихся высотных отметок дна реки с помощью процедуры SfM-MVS

Авторами были созданы карты кажущихся высотных отметок дна реки для участков 1 и 2 с помощью коммерческого программного обеспечения Agisoft PhotoScan Professional version 1.2.6. Сначала выполнялась автоматическая обработка изображений с определением структуры объекта по отображению движения (SfM) для оценки внешних и внутренних параметров камеры, а также координат для разреженных облаков точек. Наземные контрольные точки (НКТ) использовались для задания внешней системы координат и настройки некоторых внутренних параметров камеры. Затем для получения плотных облаков точек было выполнено получение многовидовых (стерео) изображений (MVS). И наконец, были созданы ортофотопланы и цифровые модели местности для обоих участков, причем их затопленные зоны были «извлечены вручную» для дальнейшего анализа.

Пространственная интерполяция высотных отметок поверхности воды

Авторы построили модель расчетных высотных отметок поверхности воды (ВПВ), используя разные методы для участков 1 и 2.

На первом участке модель ВПВ была создана путем извлечения точек уреза воды из ортофотоплана и цифровой модели местности. Были выделены соответствующие точки там, где урез воды был четко виден на ортофотоплане. На этой основе была выполнена интерполяция методом тренда для построения двумерной модели предполагаемых высотных отметок поверхности воды.

На втором участке, где урез воды не мог быть точно определен визуально по ортофотоплану (из-за нависающей растительности), была использована обычная методика измерений высотных отметок точек на урезе воды in situ (например, методом RTK-GPS). А затем был применен метод линейной интерполяции для построения одномерной модели предполагаемых высотных отметок поверхности воды вдоль русла реки.

Распределение точек вдоль уреза воды с определенными высотными отметками на обоих участках показано на рисунке 1.

Применение эмпирической поправки на рефракцию

Было испробовано четыре метода коррекции на рефракцию, чтобы сравнить их эффективность.

Метод 1 фактически соответствует случаю без коррекции: кажущаяся высотная отметка, оцененная с помощью процедуры SfM-MVS, рассматривается как отметка с поправкой на рефракцию.

Методы 2 и 4 – это существующие методы, а метод 3 был предложен авторами настоящей статьи. В этих методах поправка на рефракцию основывается на следующей формуле:

где p – коэффициент усиления рефракции (поправочный коэффициент, CF), h_R и h_A – реальная и кажущаяся глубина воды соответственно. Они оцениваются следующим образом:

Формула (4) дает возможность получить поправку на рефракцию (преломление) на поверхности воды с использованием четырех вышеуказанных методов. Рассмотрим их подробнее.

1. При методе 1 в формуле (4) используются значения p=1 и β=0 (то есть нет коррекции).

2. При методе 2, предложенном в работе [9] и традиционно используемом другими авторами [6], применяются величины p=1,34 и β=0 (где значение 1,34 является относительным показателем преломления для границы раздела «воздух – вода»).

3. При эмпирическом методе 3, предложенном авторами настоящей статьи, оценивается только величина p и принимается, что β=0.

4. При методе 4, предложенном в работе [11]:

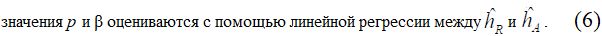
Расчеты высотных отметок дна с коррекцией на рефракцию

Чтобы построить расчетную карту рельефа дна реки с коррекцией на рефракцию, авторы воспользовались процедурой, основанной на существующем методе [9]. Первым шагом было создание расчетной карты кажущейся глубины воды путем вычитания карты кажущихся высотных отметок дна из карты высотных отметок поверхности воды (ВПВ). Затем значения карты кажущейся глубины воды были умножены на эмпирическую величину поправочного коэффициента в отношении рефракции, чтобы получить карту глубины воды с коррекцией на преломление. И наконец, чтобы создать карту рельефа дна с коррекцией на рефракцию, авторы вычли карту глубины воды с коррекцией на преломление из исходной оцененной карты ВПВ.

Оценка ошибок и сравнение результатов

Авторы сравнили среднеквадратические и средние ошибки для скорректированных высотных отметок дна с использованием четырех указанных ранее методов для обоих исследованных участков. Чтобы оценить эти ошибки для методов 3 и 4, была проведена перекрестная проверка (валидация), которая состояла из 1000 пробных  (тестовых) калибровок/прогнозов. При каждом таком виртуальном испытании подводные точки с имеющимися результатами GPS-измерений были случайным образом разделены на обучающие и тестовые данные. Формула коррекции была откалибрована для p и β (в соответствии с методом 4) с применением обучающих данных, а затем использована для прогнозирования реальной глубины воды h_R по тестовым данным. Среднеквадратические ошибки погрешностей прогнозирования для 1000 указанных виртуальных испытаний оценивались для каждого из четырех методов для каждого из исследованных участков. Поскольку использование результатов многих GPS-измерений для подводных точек в целях калибровки в практических приложениях нежелательно, авторы выполнили перекрестную проверку для различных количеств обучающих данных.

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Пригодность процедуры SfM-MVS для незатопленных зон

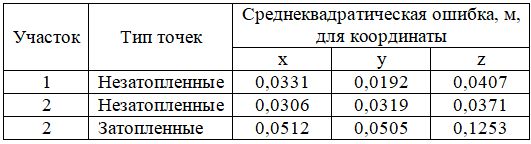
На рисунке 2 (а) в качестве примера показана карта кажущихся высотных отметок, созданная с помощью обычной процедуры SfM-MVS для участка 1. В таблице 1 приведены среднеквадратические ошибки для координат x, y, z точек, не использовавшихся в качестве наземных контрольных точек (НКТ) и оцененных путем GPS-измерений (см. рис. 1). Для незатопленных зон среднеквадратические ошибки (СКО) по каждой оси составляли в среднем около 0,03 м для обоих исследованных участков и были того же порядка, что и общая ошибка измерений методом RTK-GPS, что продемонстрировало успех использования процедуры SfM-MVS для сухих зон.

Рис. 2. Примеры полученных карт для участка 1: а – карта кажущихся высотных отметок, полученная с помощью процедуры SfM-MVS; б – карта высотных отметок дна реки, скорректированная на рефракцию с помощью предложенного метода 3 (по [1])

Таблица 1. Среднеквадратические ошибки для координат x, y, z точек, не использовавшихся в качестве наземных контрольных точек (НКТ) и оцененных путем GPS-измерений (по [1])

Необходимость коррекции на рефракцию

В таблице 1 также приведены СКО для кажущихся высотных отметок дна реки, полученные с помощью процедуры SfM-MVS для 10 подводных черно-белых меток (марок) на участке 2. Можно заметить, что СКО для горизонтальных направлений (осей X и Y) увеличились всего в 1,6 раза. С другой стороны, в вертикальном направлении (по оси Z) среднеквадратические ошибки увеличились более чем в 3,4 раза. Это говорит о том, что эффект преломления увеличивает ошибки в основном для вертикальной координаты (по оси Z), и указывает на важность коррекции для координаты z, что и является темой настоящей статьи.

Статистика ошибок для четырех методов коррекции

На рисунке 2 (б) представлена карта рельефа дна реки для участка 1, скорректированная с помощью метода 3. На рисунке 3 показаны среднеквадратические и средние ошибки, оцененные для обоих исследованных участков для каждого из четырех указанных выше методов с помощью описанной ранее перекрестной проверки (валидации) для методов 3 и 4.

Рис. 3. Среднеквадратические (СКО) и средние (СО) ошибки, оцененные в пределах исследованных участков 1 (а) и 2 (б) для каждого из четырех методов путем перекрестной проверки для методов 3 и 4 при разных количествах обучающих данных (по [1])

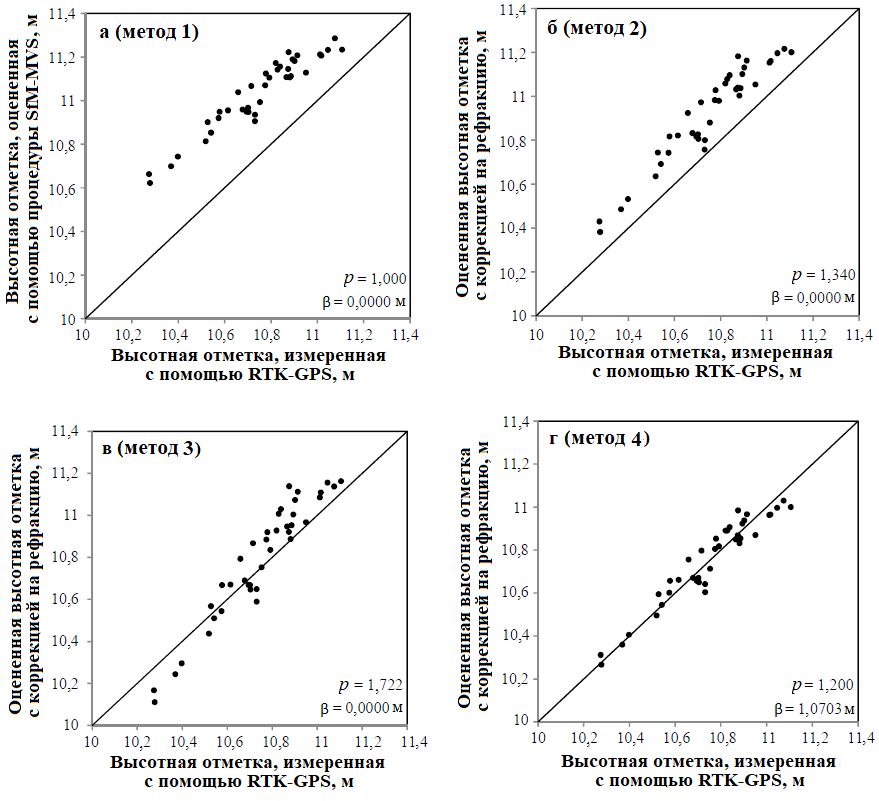
Рис. 4. Связь между оцененными высотными отметками с коррекцией и измеренными высотными отметками с помощью RTK-GPS для участка 1 при использовании методов: 1 (а), 2 (б); 3 (в); 4 (г). Для методов 3 и 4 показана степень соответствия, а не эффективность прогноза, поскольку для калибровки в этих случаях использовались все представленные на соответствующих графиках данные. Буквенные обозначения: p – поправочный коэффициент (CF); β – дополнительная поправка (невязка, offset, см. формулы (4, 5)) (по [1])

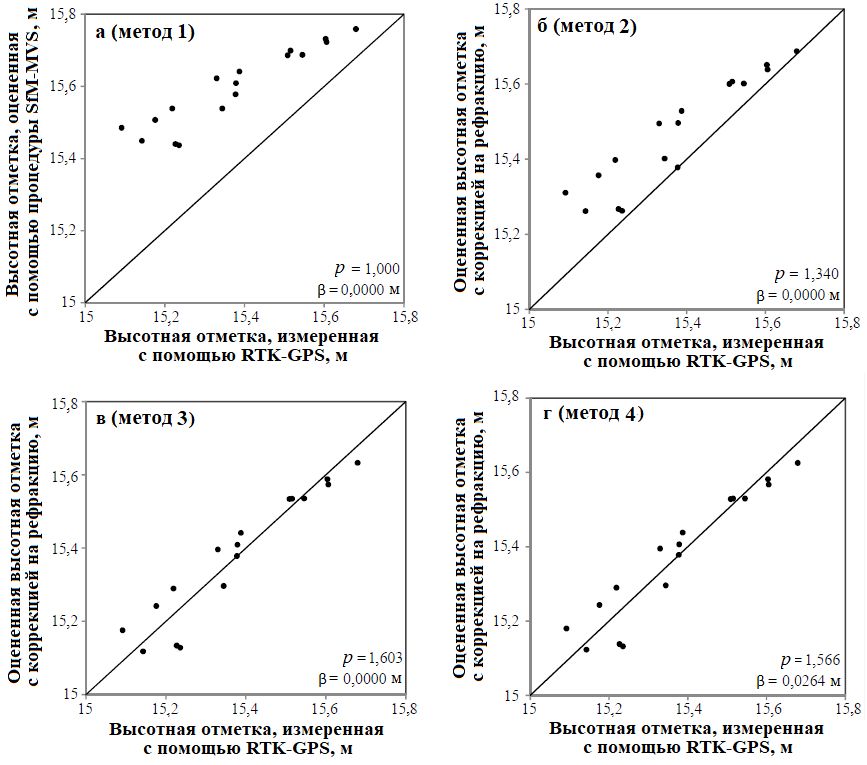
Рис. 5. Связь между оцененными высотными отметками с коррекцией и измеренными высотными отметками с помощью RTK-GPS для участка 2 при использовании методов: 1 (а), 2 (б); 3 (в); 4 (г). Для методов 3 и 4 показана степень соответствия, а не эффективность прогноза, поскольку для калибровки в этих случаях использовались все представленные на соответствующих графиках данные. Буквенные обозначения: p – поправочный коэффициент (CF); β – дополнительная поправка (невязка, offset, см. формулы (4, 5)) (по [1])

Рисунок 3 доказывает, что в целом метод 1 привел к наибольшим среднеквадратическим и средним ошибкам (за исключением случая, когда при методе 4 была выполнена калибровка только с использованием двух обучающих данных) из-за систематического завышения результатов (что отразилось на большой положительной средней ошибке), вызванного пренебрежением влияния преломления. Этот результат доказывает необходимость коррекции на рефракцию.

Простая коррекция на рефракцию с использованием метода 2 привела к среднеквадратическим и средним ошибкам, которые оказались примерно на 40% меньше, чем в случае метода 1, но все равно происходило значительное систематическое завышение результатов (что также отразилось на большой положительной средней ошибке). Это продемонстрировало наличие геометрического факта, описанного во введении, согласно которому значение поправочного коэффициента 1,34 является минимально возможным и недостаточным для реального применения.

Эффективность методов 3 и 4 оказалась выше, чем у методов 1 и 2, за исключением случаев, когда обучающих данных, использованных для калибровки, было очень мало. Для этих методов (3 и 4) среднеквадратическая и средняя ошибки увеличивались по мере уменьшения количества обучающих данных, причем увеличение было более значительным для метода 4. Это статистически оправданно: чем больше степеней свободы имеет регрессионная модель, тем более ошибконеустойчивы оценки коэффициента, поэтому для хорошей работы модель требует больше обучающих данных. В результате при использовании метода 4 с двумя степенями свободы в формуле коррекции получались чрезвычайно большие ошибки, когда количество обучающих данных было равно двум (это было минимально возможное их число). С другой стороны, метод 4 давал меньшие величины среднеквадратических и средних ошибок, чем метод 3 на участке 1, когда обучающих данных было три или более.

За исключением случая, когда обучающих данных было всего два, существующий метод 4 оказался более хорошим (с точки зрения среднеквадратических ошибок) для участка 1, а предложенный новый метод 3 – для участка 2, причем независимо от количества обучающих данных (см. рис. 3, а, б). Средние ошибки показали аналогичную тенденцию. Отсюда можно сделать вывод, что наибольшая эффективность того или иного метода по сравнению с другими зависит не только от количества обучающих данных, но и от многих других факторов. Поскольку методы 3 и 4 различаются только отсутствием или наличием поправки β (невязки, offset, см. формулы (4, 5)), наилучший метод зависит от истинной величины β. Поскольку значение β зависит от ошибок при оценке кажущихся высотных отметок поверхности воды и дна, самый эффективный метод может быть разным в зависимости от участка, условий получения изображений, условий измерений с помощью GPS и т. д.

Поскольку невозможно узнать истинное значение β, авторы считают правильным выбор наилучшего метода для каждой конкретной ситуации с использованием статистических средств. Одним из рекомендуемых путей выбора является применение способа исключений по одному при перекрестной проверке (leave-one-out cross validation), причем при каждой пробном виртуальном испытании используется только один элемент данных. Таким образом можно моделировать ошибки прогнозов при поочередном использовании для калибровки всех имеющихся результатов измерений, полученных с помощью GPS.

Нереалистично малый поправочный коэффициент для участка 1

Предложенный авторами метод 3 дал реалистичные значения поправочного коэффициента как для участка 1, так и для участка 2 (см. таблицу 2). А величина этого коэффициента, полученная с помощью метода 4, была нереально маленькой для участка 1. Это могло быть связано с большим шумом, внесшим вклад в значение кажущейся глубины воды h_A, возникшим, вероятно, из-за того, что на участке 1 высотные отметки поверхности воды на ее урезе были считаны с ортофотоплана и, таким образом, содержали ошибки, вызванные нечеткостью линии уреза воды на изображениях, а также самой процедурой фотограмметрии.

Для проверки этой гипотезы был проведен еще один численный эксперимент, чтобы виртуально пронаблюдать влияние шума, внесшего вклад в значение кажущейся глубины воды h_A, на оцененный поправочный коэффициент. В этом эксперименте к величине h_A авторы добавили искусственный нормальный (с нормальным распределением) шум с нулевым средним и различными среднеквадратичными отклонениями, оценили поправочный коэффициент и наблюдали, как он изменяется в ответ на разные уровни шума. Такие виртуальные тесты были сделаны по 1000 раз для каждого метода и для каждого участка с использованием одного и того же начального числа для генератора случайных чисел. Полученные результаты обобщены на рисунке 6.

Таблица 2. Поправочные коэффициенты для каждого метода и участка (по [1])

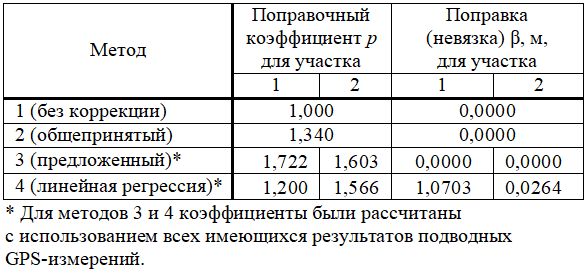
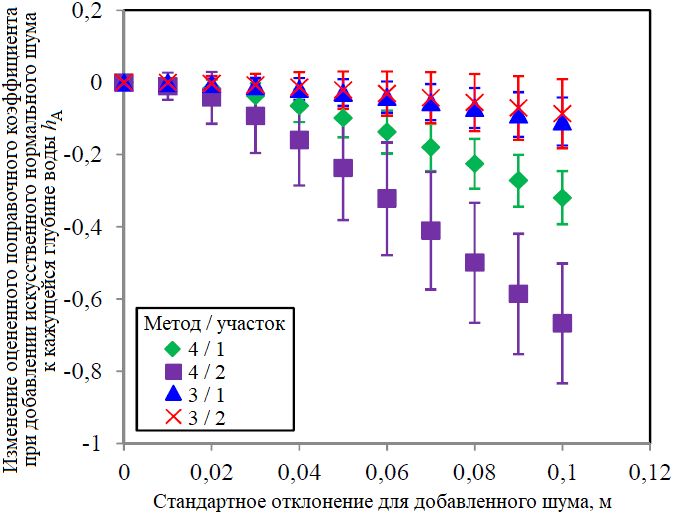
Рис. 6. Изменение оцененного поправочного коэффициента при добавлении искусственных нормальных шумов к кажущейся глубине воды h_A. Точки разной формы показывают средние значения, а «усы» (доверительные интервалы в виде отрезков) – стандартные отклонения для 1000 виртуальных тестов (по [1])

Из рисунка 6 можно увидеть, что для метода 4 среднее значение оцененного поправочного коэффициента значительно уменьшается по мере увеличения уровня шума – и это подтверждает описанную выше гипотезу. Это означает, что метод 4 дает большую отрицательную погрешность для поправочного коэффициента при зашумлении кажущейся глубины воды h_A. А для метода 3 это уменьшение поправочного коэффициента по мере увеличения уровня шума намного меньше, что свидетельствует о большей ошибкоустойчивости метода 3 к воздействию зашумления кажущейся глубины воды h_A. Этот результат указывает на превосходство метода 3 с точки зрения геометрической достоверности оцененного поправочного коэффициента.

ЗАКЛЮЧЕНИЕ

В настоящей статье был представлен эмпирический метод коррекции эффекта рефракции после обычной обработки с помощью процедуры SfM-MVS с использованием обычного программного обеспечения. В этом случае кажущаяся глубина воды преобразуется в глубину воды с поправкой на рефракцию (в реальном масштабе) путем умножения первой на эмпирический поправочный коэффициент.

Авторы проверили эффективность предложенного метода, применив его для двух участков реки и сравнив среднеквадратические и средние ошибки для скорректированных высотных отметок дна с таковыми при использовании трех существующих методов. В целом, представленный метод превзошел по эффективности два существующих метода – метод 1 ( без коррекции) и метод 2 (с использованием поправочного коэффициента, равного показателю преломления воды 1,34).

Еще один существующий метод (метод 4 – метод линейной регрессии), в котором после умножения на поправочный коэффициент добавляется эмпирическая поправка (невязка, offset, см. формулы (4, 5)), был ошибконеустойчивым, если для калибровки было очень мало обучающих данных. За исключением таких случаев, метод 4 лучше работал для участка 1 и хуже – для участка 2 по сравнению с предложенным новым методом 3. Кроме того, было обнаружено, что метод 4 имеет большую отрицательную погрешность для поправочного коэффициента при защумлении оцененной кажущейся глубины воды.

Авторы пришли к выводу, что выбор наиболее точного метода коррекции с точки зрения высотных отметок дна мелководья зависит от многих факторов (например, от участка, условий получения изображения, условий измерений с помощью GPS) и должен делаться с использованием статистических инструментов, например путем исключений вариантов по одному при перекрестной проверке (leave-one-out cross validation).

-

Эта работа была поддержана грантом JSPS KAKENHI № JP16K21194.

ИСТОЧНИКИ (REFERENCES)

1. Partama I.G.Y., Kanno A., Akamatsu Y., Inui R., Goto M., Sekine M. A simple and empirical refraction correction method for UAV-based shallow-water photogrammetry // Geological and Environmental Engineering: International Journal. World Academy of Science, Engineering and Technology (WASET), 2017. Vol. 11. № 4. Paper 32268. URL: publications.waset.org/10006734/pdf.
2. Monica R.V., Rocio B.G., Thomas K., Amanda V. Automated Identification of River Hydromorphological Features Using UAV High Resolution Aerial Imagery // Sensors. 2015. Vol. 15. P. 27969–27989.
3. Nagata N., Hosoda T., Muramoto Y. Numerical analysis of river channel processes with bank erosion // Journal of Hydraulic Engineering. 2000. Vol. 126. № 4. P. 243–252.
4. Ulrich K., Rainer B., Konrad H. Assessment of river habitat in Brandenburg, Germany // Limnologica. 2004. Vol. 34. P. 176–186.
5. Legleiter C.J., Kyriakidis P.C. Spatial prediction of river channel topography by kriging // // Earth Surface Processes and Landforms. 2008. Vol. 33. № 6. P. 841–867.
6. Woodget A.S., Carbonneau P.E., Visser F., Maddock I.P. Quantifying submerged fluvial topography using hyperspatial resolution UAS imagery and structure from motion photogrammetry // Earth Surface Processes and Landforms. 2015. Vol. 40. P. 47–64.
7. Butler J.B., Lane S.N., Chandler J.H. Through-water close range digital photogrammetry in flume and field environments // Photogrammetric Record. 2002. Vol. 17. № 99. P. 419–439.
8. Fryer J.G., Kniest H.T. Error in depth determination caused by waves in through-water photogrammetry // Photogrammetric Record. 1985. Vol. 11. № 66. P. 745–753.
9. Westway R.M, Lane S.N., Hicks D.M. The development of an automated correction procedure for digital photogrammetry for the study of wide, shallow, gravel-bed rivers // Earth Surface Processes and Landforms. 1999. Vol. 25. P. 209–226.
10. Murase T., Tanaka M., Tani T., et al. A photogrammetric correction procedure for light refraction effects at a two-medium boundary // Photogrammetric Engineering & Remote Sensing. 2008. Vol. 74. № 9. P. 1129–1136.
11. Bagheri O., Ghodsian M., Saadatseresht M. Reach scale application of UAV+SfM method in shallow rivers hyperspatial bathymetry // Proceedings of the International Conference on Sensors & Models in Remote. 2015. Vol. 40. P. 23–25.