Определение модулей деформации при трехосном сжатии

Одной из основных задач механики грунтов является определение перемещений в основаниях различных сооружений. Расчетом абсолютных перемещений (осадки, горизонтального смещения), а также относительных перемещений (разности осадок, крена) определяют возможность нормальной эксплуатации сооружения. Такие расчеты требуют выбора некоторой механической модели деформирования – закономерности развития деформаций в зависимости от изменения напряжений.

Деформируемость грунтов является комплексным явлением, что обусловлено их многофазностью: твердые частицы образуют пространственную структуру – скелет, поры которого заполнены жидкостью или газом. При уплотнении происходит уменьшение объема пор, сокращается расстояние между частицами, увеличивается плотность их упаковки. На данном этапе наблюдаются исключительно объемные деформации. Дальнейшее уплотнение грунта невозможно без взаимного смещения частиц, при котором более мелкие частицы занимают более крупные поры. При этом развиваются сдвиговые деформации, приводящие к уменьшению объема. Это явление характерно исключительно для дисперсных сред. На последнем этапе уплотнение происходит за счет сжатия самих частиц, однако при строительных уровнях напряжений это наблюдается редко, а величина деформаций настолько мала, что ею можно пренебречь.

Абсолютное большинство моделей деформирования в механике грунтов являются феноменологическими, то есть описывают реакцию среды на воздействие на основании экспериментальных наблюдений, не рассматривая внутренних механизмов взаимодействия различных фаз. Как известно, простейшей из таких моделей является модель линейного деформирования Р. Гука (1660). Приращения напряжений и деформаций в сплошной изотропной деформируемой среде связаны между собой линейной зависимостью. Коэффициент пропорциональности этой зависимости называется модулем упругости и обозначается Е:

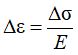
В случае трехосного НДС необходимо учитывать также влияние напряжений и деформаций в направлениях, перпендикулярных рассматриваемому. В этом случае вводится величина μ, называемая коэффициентом Пуассона и определяющая способность материала к поперечным деформациям. С использованием этих двух величин могут быть записаны физические уравнения, связывающие между собой компоненты напряжений и деформаций – закон Гука в общем виде:

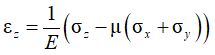
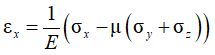
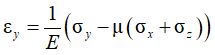
К моменту начала развития расчетов осадок оснований на базе модели линейного деформирования уже был создан развитый математический аппарат теории упругости. Это предопределило его применение для описания поведения грунта при деформировании, но, в свою очередь, потребовало введения понятий элементарного представительного объема грунта и предположения об изотропности свойств, о которых можно подробнее узнать из любого учебного пособия.

Кроме того, в грунтах преобладают пластические деформации, их достоверная оценка выходит на первый план по сравнению с конструкционными материалами искусственного происхождения. Количественная оценка величины пластических деформаций аналитическими методами представляет достаточно сложную задачу, чаще для этой цели пользуются численными методами решения. В действующих нормативно-технических документах вместо этого предлагается ограничение предельно допустимой нагрузки на основание такой величиной давления, до достижения которого можно пренебречь нелинейностью деформирования – расчетным сопротивлением R. Такое упрощение позволяет использовать при расчете оснований теорию линейно-деформируемого пространства.

В связи с тем, что развитие деформаций в грунте чаще происходит по нелинейному закону, а пластические деформации начинают развиваться практически сразу, модуль E некорректно называть модулем упругости. В механике грунтов пользуются термином «модуль общей деформации», или «модуль линейной деформации», обозначаемым E₀ и подразумевающим, что учитываются и упругие, и пластические деформации грунта, но предполагается линейный закон деформирования. Аналогично и коэффициент Пуассона μ заменяется коэффициентом относительного поперечного расширения ν. Это позволяет избежать терминологической путаницы между параметрами грунта как линейно-деформируемого тела и параметрами упругости, которые могут быть определены для некоторых разновидностей грунтов, например, геофизическими методами.

Необходимо помнить, что ни один механический параметр нельзя определять в отрыве от выбранной механической модели грунта. Так, например, модуль общей деформации устанавливает линейную зависимость между напряжениями и деформациями, которая в реальных грунтах может не наблюдаться. Модуль деформации не является параметром грунта – это параметр механической модели, описывающей поведение грунта в конкретном диапазоне напряжений.

Остаточные деформации при разгрузке составляют значительную часть от общей деформации. СП 22.13330.2016 предписывает учитывать это обстоятельство при глубинах котлована более 5 м. Для таких случаев определяются параметры деформируемости по ветви разгрузки и повторного нагружения – модуль в этом случае обозначается E_ur.

Модуль общей деформации Е₀ определяется по результатам трехосных испытаний в консолидированно-дренированном режиме в полном соответствии с законом Гука для осесимметричного напряженного состояния:

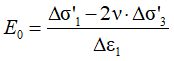
Но в связи с тем, что определение выполняется на этапе девиаторного нагружения при постоянном давлении в камере, Δσ₃ = 0, формула сводится к более простому виду, представленному в ГОСТ:

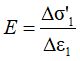
Из вышесказанного следует, что использование других траекторий нагружения (Δσ₃ ≠ 0) требует соответствующих изменений формулы для расчета модуля деформации.

Основные сложности традиционно вызывает выбор диапазона напряжений для определения модуля деформации. Формально модуль деформации может быть определен в любой момент испытания, если этого требует техническое задание. ГОСТ 12248-2010 при этом никаких рекомендаций не содержит, в нем приводится только пример графического построения (см. рис. И.2 ГОСТ 12248-2010). Из данного рисунка большинством специалистов делается вывод о том, что модуль деформации определяется на «некотором линейном участке». Это принципиально неверно, а причина заблуждения кроется в неудачном оформлении графиков ГОСТ.

Рис. 1. Определение модуля деформации согласно ГОСТ 26518-85 и ГОСТ 12248-2010

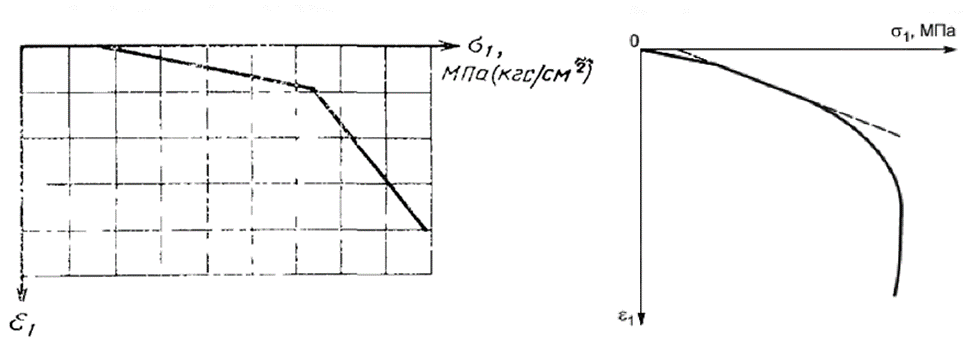
Впервые рекомендации по определению модуля деформации в ходе трехосных испытаний были приведены в ГОСТ 26518-85. График строился в координатах «полные вертикальные напряжения σ₁ – относительные деформации ε₁», и был аппроксимирован двумя прямыми отрезками. Примечательно, что началом графика является нулевое значение относительных деформаций, но не нулевое значение напряжений – то есть к образцу уже приложено некоторое напряженное состояние, а вызванные деформации обнулены. Это полностью соответствует тексту ГОСТ 12248-2010, предполагающему, что относительные деформации рассчитываются от высоты образца после завершения консолидации.

В последующих редакциях ГОСТ (после объединения он получил номер 12248) та же иллюстрация была приведена уже с ошибкой: график начинается из начала координат, что противоречит тексту документа. В результате положение отрезка линейной аппроксимации никак не регламентировано, «повисает в воздухе», и модуль деформации по результатам трехосных испытаний может быть определен, фактически, как угодно – на усмотрение сотрудника лаборатории.

В готовящейся актуализированной редакции ГОСТ 12248.3 этот недостаток устранен. Первой точкой диапазона определения модуля деформации следует принять точку начала девиаторного нагружения (моделирующего дополнительную нагрузку от сооружения) – то есть начальное напряженное состояние в массиве. При девиаторном нагружении в образце преобладают деформации сдвига, что делает бессмысленным поиск каких-либо «условно-линейных» отрезков на зависимости. Вместо этого следует задаться некоторой фиксированной точкой по напряжениям или деформациям. Для деформаций это могла бы быть величина, примерно соответствующая диапазону работы реальных оснований (2-4%). Но в практических целях было принято решение использовать фиксированную точку по напряжениям, соответствующую 60% от бытовых вертикальных напряжений. Такой подход не только формализует процедуру определения модуля деформации, но и упрощает сопоставление результатов, полученных различными лабораториями в кинематическом или статическом режимах нагружения.

В результате построение для определения модуля деформации в готовящейся редакции ГОСТ 12248.3 представлено в следующем виде:

Рис. 2. Определение модуля общей деформации и модуля деформации разгрузки согласно проекту ГОСТ 12248.3

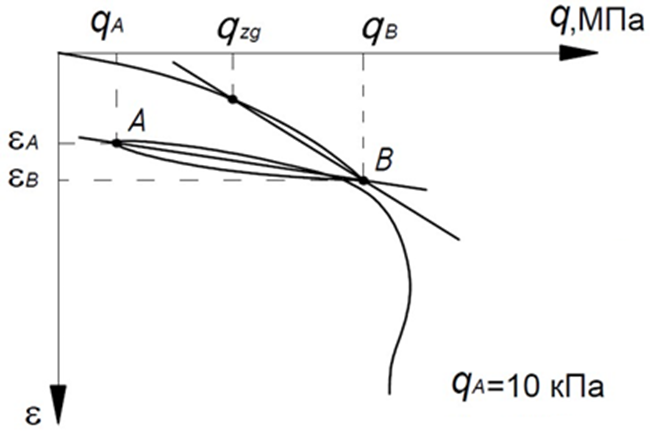
При изотропной консолидации девиатор в начале опыта отсутствует, и q_zg = 0. Вторая точка диапазона q_B на 60% больше бытового вертикального давления; данная величина принята для удобства сопоставления испытаний с кинематическим и ступенчатым приложением нагрузки. Разгрузка выполняется до величины девиатора 10 кПа, чтобы при использовании более распространенной камеры типа А сохранялся контакт штока и штампа. При анизотропной консолидации девиатор в начале опыта не равен 0, но диапазон определения модуля все равно на 60% больше бытового вертикального давления. Разгрузка в этом случае выполняется до величины девиатора также 10 кПа, то есть уходит ниже точки бытового напряженного состояния в предположении, что это больше соответствует диапазону изменения напряжений в основании.

Модуль разгрузки и повторного нагружения Eur определяется аналогично, но на ветви разгрузки. При этом, как и в случае первичного нагружения, разгрузку следует выполнять либо ступенями с выдержкой до стабилизации, либо кинематически, но с той же скоростью, что при первичном нагружении. В противном случае возможно опасное завышение модуля разгрузки, так как процесс упругой разгрузки скелета требует увеличения объема пор и подчиняется законами фильтрационной консолидации (всасывание жидкости происходит во времени).

В расчетах в целях упрощения предполагается, что при повторном нагружении модуль будет таким же вплоть до выхода на ветвь первичного нагружения, однако опытами это не подтверждается. Экспериментально доказано, что величина модуля разгрузки непостоянна, и зависит от степени приближения к предельному сопротивлению сдвигу – тем не менее, в аналитических и численных расчетах это обстоятельство не учитывается.

В последнее время поднимается вопрос о необходимости введения дополнительных коэффициентов корреляции между значениями модулей деформации, определенными в ходе трехосных и штамповых испытаний. Действительно, с теоретической точки зрения при девиаторном нагружении в стабилометре преобладают деформации сдвига, а уплотнение грунта под штампом (или реальным фундаментом) происходит в первую очередь за счет изменения объема пор. Тем не менее, нельзя отрицать, что в ходе нагружения основания штампом в основании практически сразу возникают касательные напряжения, приводящие к сдвиговой деформации. В приборе трехосного сжатия на начальном этапе нагружения (где обычно и определяется модуль деформации) имеет место объемное сжатие образца, что подтверждается экспериментально. Таким образом, в рамках принятой теории линейного деформирования расхождение между значениями модуля, полученными этими двумя методами, скорее вызвано ошибками при выборе диапазона определения, а не различием механизмов деформирования.

Для определения модуля деформации в условиях трехосного сжатия ООО НПП «Геотек» предлагает в составе комплексов АСИС серию как стандартных, так и специализированных установок (стабилометров). Установки могут быть оснащены камерами объемного (тип «А») и радиального (тип «Б») сжатия для создания трехосного напряженного состояния, а также необходимым оборудованием для создания вертикального силового воздействия, управления камерным и противодавлением. Испытания проводятся в автоматизированном режиме с контролем всех параметров испытания в режиме реального времени.

Более подробную техническую информацию можно получить у специалистов компании или на сайте www.npp-geotek.ru

Список литературы

ГОСТ 12248-2010. Грунты. Методы лабораторного определения характеристик прочности и деформируемости.

ГОСТ 26518-85. Грунты. Метод лабораторного определения характеристик прочности и деформируемости при трехосном сжатии.

ISO 17892-9:2018. Geotechnical investigation and testing — Laboratory testing of soil — Part 9: Consolidated triaxial compression tests on water saturated soils.

Бершов А.В., Мирный А.Ю., Усов А.Н. Определение модуля деформации разгрузки в дисперсных грунтах и его учет при проектировании.

Болдырев Г.Г. Методы определения механических свойств грунтов с комментариями к ГОСТ 12248-2010. М.: Прондо, 2014.

Мирный А.Ю. Аналитическое сопоставление методов прямого определения параметров деформируемости грунта. Геотехника, № 1, 2018.

Ухов С.Б. и др. Механика грунтов, основания и фундаменты. М.: АСВ, 2005