Об использовании метода пространственного усреднения для дискретизации случайных полей

Введение

С помощью метода пространственного усреднения (spatial averaging, SA) можно представить случайное поле (random field, RF) через набор случайных величин, представляющих собой локальные средние значения этого поля. Первоначально этот метод был предложен Ванмарке и Григориу (Vanmarcke, Grigoriu, 1983), затем он был подробно описан в монографии Ванмарке (Vanmarcke, 2010).

Метод пространственного усреднения применяется к однородным случайным полям в различных приложениях и обычно используется в контексте геотехнического анализа для аппроксимации пространственно изменяющихся свойств грунта (Rackwitz, 2000;  Fenton, Griffiths, 2003, 2005; Ching, 2016; Tabarroki et al., 2021). Преимущество здесь заключается в том, что поведение оснований сооружений может определяться средними, а не локальными свойствами грунта. Поэтому случайные поля зачастую можно достаточно хорошо аппроксимировать небольшим набором случайных величин или даже одной случайной величиной, отражающей усредненное поведение случайного поля в пространственной области (например, для плоскости разрушения).

Метод пространственного усреднения может быть применен и к неоднородным случайным полям, например в контексте анализа надежности (Geyer et al.,, 2019; Papaioannou et al., 2019).

Неоднородные случайные поля возникают, например, когда функции пространственного момента (среднее значение и дисперсия) следуют некоему тренду или когда однородное случайное поле обновляется включением данных измерений с помощью байесовского анализа (Geyer et al., 2022).

Сочетая моделирование случайного поля и байесовский анализ для учета имеющихся данных, можно определить точную вероятностную модель свойств материала для анализа надежности конструкции. Однако для этого надо выполнить все необходимые стадии расчетов с использованием полной модели случайного поля, которая является дорогостоящей с точки зрения вычислений и которую нелегко совместить с большинством коммерческих программ, работающих на основе метода конечных элементов (Geyer et al., 2019). Сложность этой модели может быть уменьшена за счет использования дискретизации, то есть представления случайного поля через конечное количество случайных величин. Существует множество групп методов дискретизации (точечной дискретизации, усредненной дискретизации, расширения рядов) (Sudret, Der Kiureghian, 2000).

Далее будет рассмотрен метод пространственного усреднения (Vanmarcke, 2010) для дискретизации случайных полей, полученных при измерениях с пространственной переменной, c применением нового подхода, предложенного и описанного в последние годы Гейером с соавторами (Geyer et al., 2019, 2020, 2022). Сначала для обновления модели случайного поля использовались прямые измерения интересующего параметра. Затем выполнялось сведение неоднородного случайного поля к набору случайных величин с помощью пространственного усреднения. Данный подход учитывает пространственную корреляцию расположения точек измерений в байесовском анализе, а дискретизация неоднородного случайного поля позволяет напрямую применять коммерческое конечноэлементное программное обеспечение в процессе анализа надежности.

Метод пространственного усреднения для дискретизации случайных полей

Для точного представления случайного поля в любой точке обычно требуется «бесконечное» число случайных величин. А с помощью методов дискретизации случайное поле аппроксимируется в виде конечного количества случайных величин. Для этого был предложен метод Ванмарке (Vanmarcke, 2010), который легко использовать на практике. В этом методе случайное поле представляется как набор локальных интегралов, которые соответствуют средним значениям случайного поля для небольших участков области W. Для наглядности рассмотрим одномерный случай (хотя эта концепция применима и к многомерным вариантам).

Пространственное среднее значение X_Ti случайного поля X(t) в интервале [t₁, t₂] определяется следующим образом (Vanmarcke, 2010):

где T_i – длина области интегрирования, то есть T_i = t₂ – t₁.

На рисунке 1 в графическом виде представлено однородное гауссово случайное поле и среднее пространственное значение X_Ti в интервале [t₁, t₂] длиной T_i, определяемой уравнением (1). Можно показать, что случайное поле X(t) аппроксимируется постоянным значением в интервале [t₁, t₂].

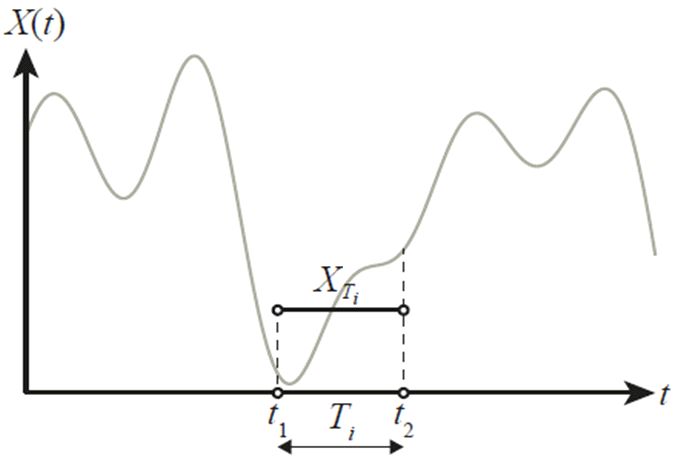
Рис. 1. Аппроксимация случайного поля X(t) через локальное пространственное усреднение в интервале [t₁, t₂]

Соответственно, может быть определено общее среднее локальных пространственных средних значений:

Если величина μ_X(t) постоянна в пространстве (например, в однородном случайном поле), то это интегрирование не влияет на среднее значение. Отметим, что:

Напротив, процесс усреднения всегда влияет на дисперсию случайного поля. Для однородного случайного поля ее можно вычислить путем умножения дисперсии случайного поля на коэффициент уменьшения, найденный путем интегрирования по функции автокорреляции, которая является функцией только пространственного расстояния (Vanmarcke, 2010). Эту функцию часто называют функцией уменьшения дисперсии.

Однако в неоднородном случае корреляция двух точек может зависеть не только от их пространственного расстояния и дисперсии случайного поля (которая не является постоянной в пространстве). Следовательно, дисперсия усредняющего интеграла должна быть вычислена с помощью следующего двойного интеграла по функции автоковариации:

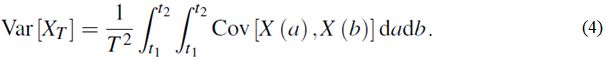
Чтобы представить случайное поле с использованием элементов локального пространственного усреднения, необходимо правильно учитывать ковариацию и, следовательно, корреляцию этих локальных средних значений.

Рассмотрим два интервала длиной T₁ и T₂, для которых необходимо рассчитать ковариацию, как показано на рисунке 2. Ковариация двух пространственных средних Cov[X_T2, X_T1] может быть рассчитана на основе локальных усредненных отклонений следующим образом (Vanmarcke, 2010):

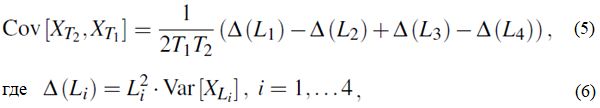
где L₁, L₂, L₃, L₄ – расстояния между конечными точками интервалов T₁ и T₂ на рисунке 2.

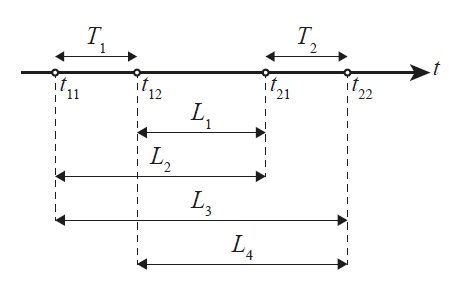
Рис. 2. Интервалы для вычисления ковариации локальных интервалов усреднения Т₁ и Т₂

Локальные усредненные отклонения уравнения (6) вычисляются с помощью уравнения (4). Следует отметить, что формула (5) также справедлива для перекрывающихся, содержащих друг друга или совпадающих интервалов T₁ и T₂.

На основе уравнений (3–6) могут быть вычислены все необходимые параметры локальных усредненных случайных величин, используемых для представления гауссова случайного поля. Аппроксимация случайного поля, представленного на рисунке 1, с помощью метода пространственного усреднения с пятью элементами проиллюстрирована на рисунке 3. Случайное поле аппроксимируется набором из пяти случайных величин, которые следуют многомерному распределению Гаусса со средним вектором и ковариационной матрицей, рассчитанной в соответствии с уравнениями (3–6).

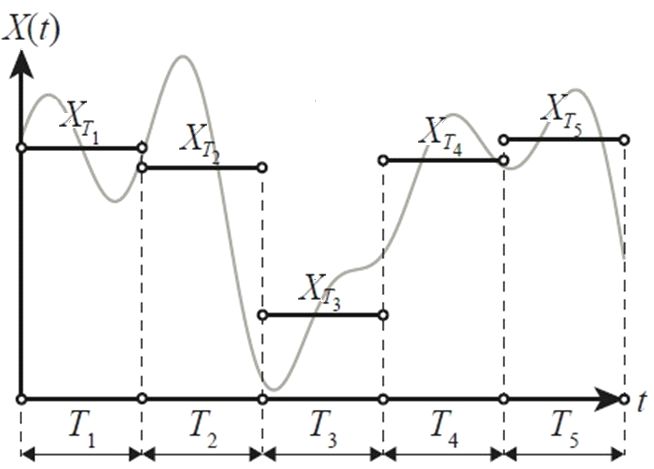
Рис. 3. Аппроксимация случайного поля X(t) с помощью метода пространственного усреднения с пятью элементами (n_SA = 5)

Число элементов, используемых для усреднения, определяет точность аппроксимации. Для количественной оценки ошибки аппроксимации, то есть разницы между истинным случайным полем и аппроксимированным, могут использоваться различные меры погрешности, например дисперсия ошибки, смещение, среднеквадратичная ошибка (Sudret, Der Kiureghian, 2000; Betz et al., 2014 и др.). Поскольку эти величины обычно определяются по точкам, глобальные меры погрешности могут быть вычислены путем интегрирования (Sudret, Der Kiureghian, 2000). Требуемое количество элементов для метода пространственного усреднения можно определить, установив целевую глобальную ошибку дискретизации.

Заключение

Пространственная изменчивость свойств грунтов является одним из источников неопределенностей в результатах инженерных изысканий. Она может быть смоделирована с помощью теории случайных полей, в соответствии с которой тот или иной параметр грунта в любой области инженерно-геологического элемента является случайной переменной, характеризующейся вероятностной функцией распределения. Анализ неоднородного случайного поля интересующего показателя можно упростить, подвергнув это поле дискретизации и применив метод пространственного усреднения для отдельных его областей, то есть сведя представление поля к набору случайных величин, являющихся локальными средними значениями для этих областей (в идеале используя самые элементарные области, хотя их количество зависит от требуемой точности аппроксимации).

Указанный метод полезно использовать в процессе геотехнического анализа для аппроксимации пространственно изменяющихся свойств грунта, особенно для структурного анализа при совместном использовании модели случайного поля и метода конечных элементов.

Список литературы

1. Betz W., Papaioannou I., Straub D., 2014. Numerical methods for the discretization of random fields by means of the karhunen-loиve expansion // Computer Methods in Applied Mechanics and Engineering. 2014. Vol. 271. P. 109–129.
2. Ching J., Tong X.-W., Hu Y.-G., 2016. Effective Young's modulus for a spatially variable soil mass subjected to a simple stress state // Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards. 2016. Vol. 10. № 1. P. 11–26.
3. Fenton G.A., Griffiths D.V., 2003. Bearing-capacity prediction of spatially random c-φ soils // Canadian Geotechnical Journal. 2003. Vol. 40. № 1. P. 54–65.
4. Fenton G.A., Griffiths D.V., 2005. Three-dimensional probabilistic foundation settlement // Journal of Geotechnical and Geoenvironmental Engineering. 2005. Vol. 131. № 2. P. 232–239.
5. Geyer S., Papaioannou D., Straub I., Kunz, C., 2019. Bayesian reliability assessment with spatially variable measurements: the spatial averaging approach // J. Song (ed.). Proceedings of the 13th International Conference on Application of Statistics and Probability in Civil Engineering. Seoul: Seoul National University open repository, 2019. P. 1–8.
6. Papaioannou I., Geyer S., Straub D., 2019. Bayesian updating of foundation reliability with spatially variable measurements: a spatial averaging approach // J. Ching, D.Q. Li, J. Zhang (eds.). Proceedings of the 7th International Symposium on Geotechnical Safety and Risk. Research publishing, 2019. P. 619–624.
7. Rackwitz R., 2000. Reviewing probabilistic soils modelling // Computers and Geotechnics. 2000. Vol. 26. № 3. P. 199–223.
8. Sudret B., Der Kiureghian A., 2000. Stochastic finite element methods and reliability: a state-of-the art report // Structural Engineering, Mechanics and Materials. Berkeley, USA: University of California, Department of civil and environmental engineering, November 2000. Report № UCB/SEMM-2000/08. 190 р. URL: bruno.sudret.free.fr/docs/2000%20-%20State-of-the-art%20Stochastic%20Finite%20Elements%20and%20Reliability.pdf.
9. Tabarroki M., Ching J., Phoon K.-K., Chen Y.-Z., 2021. Mobilisation-based characteristic value of shear strength for ultimate limit states // Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards. 2021. Vol. 0. P. 1–22.
10. Vanmarcke E., Grigoriu V., 1983. Stochastic finite element analysis of simple beams // Journal of Engineering Mechanics. 1983. Vol. 109. № 5, P. 1203–1214.
11. Vanmarcke T., 2010. Random fields: analysis and synthesis, revised and expanded. New Edition. World Scientic, 2010. 364 p.