О программном средстве для практического применения геостатистики в геологии и геотехнике. Часть 1
 Болдырев Геннадий ГригорьевичДиректор по научной работе и инновациям ООО НПП «Геотек», г. Пенза, Россияg-boldyrev@npp-geotek.ru
Болдырев Геннадий ГригорьевичДиректор по научной работе и инновациям ООО НПП «Геотек», г. Пенза, Россияg-boldyrev@npp-geotek.ruГеостатистика как раздел статистики учитывает пространственные корреляции, встречающиеся во многих геологических и геотехнических исследованиях. Из таких корреляций можно извлечь ценную информацию, что в том числе помогает справиться с проблемой ограниченного объема исходных данных. Но это часто бывает связано с отсутствием удобного для пользователей программного обеспечения, препятствующего применению геостатистики.
В соответствии с насущностью данной проблемы представляем вниманию читателей большую статью, посвященную работе в программном пакете GSTools v1.3, основанном на высокоуровневом языке программирования Python. Основой статьи послужили: рассмотрение материалов соответствующего обзора разработчиков этого пакета Себастьяна Мюллера и др. (Германия, Нидерланды) [1], научно-практическое переосмысление этих материалов с ориентацией на потребности российских геотехников и дополнительная поясняющая информация из других источников.
Пакет GSTools предоставляет методы для генерации случайных полей, может выполнять кригинг, оценку вариограмм и многое другое. Его можно использовать для решения задач геологии и геотехники широкого спектра. Разработчики GSTools [1] выбрали язык программирования Python из-за предоставляемого им оптимального баланса между удобством использования, гибкостью и эффективностью, а также из-за его популярности в научных кругах.
Сегодня публикуем первую часть статьи, в которой помимо вводной части рассмотрены такие функциональные возможности GSTools, как построение ковариационных моделей и вариография.

ВВЕДЕНИЕ
Геостатистика возникла как один из разделов статистики в начале 1950-х годов благодаря эмпирической работе южноафриканского горного инженера Дэни Герхардуса Криге [2], который предложил некоторые из первых методов этого специфического научного направления для оценки минеральных ресурсов. А позднее, в 1960-х годах, данное направление формализовал французский инженер Жорж Матерон [3], разработав его математические основы.
Сегодня геостатистика применяется в геологии, гидрогеологии, гидрологии, почвоведении, метеорологии, экологии, океанографии, эпидемиологии и др. [4–11]. Большое количество соответствующих пособий, инструкций и учебников делают теорию этого направления доступной для практиков [5, 12–20 и др.]. Тем не менее темпы внедрения геостатистики в практику были медленными и неравномерными [19, 20]. Одной из причин этого была нехватка подходящего геостатистического программного обеспечения [19–24]. Несмотря на то что сегодня доступно не такое уж малое количество геостатистических программных решений [25–32], их внедрению препятствуют недостаточное удобство использования и лицензирование [33].
Для решения этих проблем Себастьян Мюллер с коллегами [1, 34] разработали большой пакет программ GSTools на языке программирования Python, предназначенный для геостатистического анализа (в их работе 2022 года [1] рассматривается новая версия – GSTools v1.3). Насколько известно, в настоящее время не существует пакета Python с открытым исходным кодом, который предоставлял бы полный необходимый набор средств (функций) для генерации случайных полей, прямого моделирования, кригинга и анализа данных. Однако, с точки зрения разработчиков GSTools [1], выбранный ими язык Python потенциально может решить следующий ряд проблем, связанных с геостатистическими приложениями.
1. Такая среда разработки, как Python, позволяет достичь баланса между простотой использования (обеспечиваемой графическими пользовательскими интерфейсами [35]) и гибкостью (обеспечиваемой инструментами на основе командной строки [36–38 и др.]).
2. Python известен как язык, способный объединять независимые программные решения для выполнения сложных рабочих процессов. Это особенно важно, поскольку геостатистика часто полагается на готовые решатели для генерации данных или на решатели моделей на основе уравнений в частных производных (Partial Differential Equations – PDE).
3. Python – это простой, но мощный язык с увеличивающимся количеством пользователей и растущей поддержкой сообщества в сфере научных вычислений и анализа данных.
Таким образом, как полагают Мюллер и др. [1], язык программирования Python имеет прекрасные перспективы в обозримом будущем. Даже те инженеры и ученые, которые имеют лишь поверхностное образование в области компьютерных наук, смогут применить данный инструментарий и внести необходимые изменения в его конкретные приложения. Однако, чтобы гарантировать принятие и дальнейшее развитие этой области, необходимо максимально «разрешительное» лицензирование.
КОВАРИАЦИОННЫЕ МОДЕЛИ И ВАРИОГРАФИЯ
Как указывают Мюллер и др. [1], в программном пакете GTools реализуется мощный класс CovModel. Методы, предоставляемые этим классом, являются основой для большинства функциональных возможностей программного пакета GSTools, таких как вариография, генерация пространственных случайных полей и кригинг. Модуль CovModel представляет ковариационные модели и вариограммы [1].
Ковариационные модели
Выбор ковариационных функций (модели) зависит от характера стохастичности случайного поля. В геотехнической практике тип ковариационной модели, используемой для пространственной оценки распределения свойств грунта, часто определяется на основе большого количества результатов измерений с использованием геостатистики [14, 39].
Однако данные инженерно-геологических исследований, как правило, являются ограниченными и характеризуются низкой изученностью – в основном из-за стоимости изысканий. Из-за этого точной оценки структуры ковариационной модели достичь трудно. Поэтому в геотехническом вероятностном анализе (например, в анализе надежности оснований, склонов, подпорных стен и пр.) часто используются теоретические модели с предполагаемыми масштабами изменчивости в пространстве.
Изменчивые в пространстве свойства грунта имеют определенную корреляцию между каждыми двумя точками пространства, при этом они в целом гораздо больше коррелируют в соседних местах, чем в удаленных друг от друга [1].
В таблице 1 приведены основные ковариационные модели, применяемые в геостатистике.
Таблица 1. Одномерные функции корреляции [40]
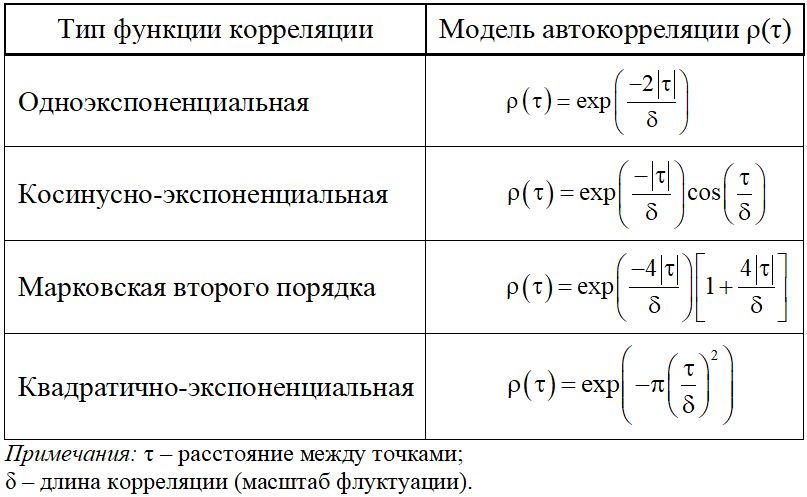
Мюллер и др. [1] использовали несколько ковариационных моделей, которые включены в модуль CovModel.
Вариограммы
Вариограмма – это график, показывающий, как изменчивость изучаемой пространственной переменной (в виде дисперсии) меняется с увеличением расстояния, и отражающий пространственную корреляцию измеренных значений в опорных, или обусловленных, точках. Она состоит из двух разных форм, связанных друг с другом и называемых экспериментальной и модельной (рис. 1). Сначала рассчитывается экспериментальная вариограмма с использованием фактически измеренных значений. Затем создается модельная вариограмма путем аппроксимации экспериментальной формы с использованием любой из общепринятых моделей, таких как линейная, сферическая, экспоненциальная и т. д. [6, 41]. Функции модельной вариограммы представлены в таблице 2.
![Рис. 1. Экспериментальная и модельная вариограммы [42]](/images/dynamic/img48039.jpg)
Таблица 2. Функции модельной вариограммы [43]

Экспериментальная вариограмма описывается следующим уравнением:
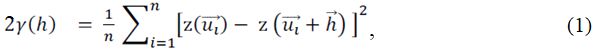
где z – анализируемая переменная (параметр); 2γ(h) – значение вариограммы при расстоянии между точками в паре h; z(u) – значение переменной в точке (u); z(u+h) – значение переменной в точке (u+h) (см. рис. 1); n – общее число пар точек; i – номер пары точек.
Вариограмма, представленная на рисунке 1, измеряет разницу (изменение, несходство) между парами переменных на расстоянии h до достижения некоего постоянного значения, которое называется порогом. Расстояние, на котором вариограмма достигает порога, называется длиной корреляции (см. рис. 1), которая определяет автокоррелированную область переменной [44].
Если вариограмма пересекает ось ординат не в ее начале, а в некоем значении 2γ(h) (см. рис. 1), то это значение еще при возникновении геостатистики (при изучении содержания золота в пробах, которое может сильно различаться, даже если они взяты совсем рядом друг с другом) получило название «эффект самородка».
Эффект самородка представляет собой кажущуюся неоднородность функции вариограммы [45] и может быть определен как мера прямой повторяемости данных, ошибки измерения, разнообразия выборки и разрозненности данных [44, 46].
Как указывают Мюллер и др. [1], GStools реализует в модуле CovModel класс ковариационных моделей слабостационарных пространственных процессов. Здесь слабая стационарность означает, что связанная с ней вариограмма ограниченна, поскольку принимаются постоянное среднее значение и конечная дисперсия.
Для аппроксимации неограниченных вариограмм, таких как модель степенного закона [47], Мюллер и др. [1] предложили набор усеченных степенных моделей на основе работы Ди Федерико и Ноймана [48]. В соответствии с этим внутреннее представление вариограммы γ задается следующей формулой:
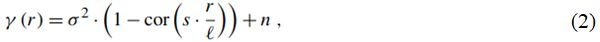
где r – (изотропное) расстояние между точками в паре, или (изотропный) лаг; l – (основная) длина корреляции; s – коэффициент масштабирования для корректировки представления модели (по умолчанию равный единице); σ2 – дисперсия, или частичный порог; n – эффект самородка, или субмасштабная дисперсия; cor(sr/l)=cor(h) – нормализованная корреляционная функция, зависящая от безразмерного расстояния h=sr/l, которая определяет модель.
Соответствующие ковариационные и корреляционные функции задаются такими формулами:

Мюллер и др. [1] обращают внимание на то, что ковариация и корреляция здесь пренебрегают эффектом самородка в начале координат. Таким образом, дисперсия интерпретируется как вариация над ним, которую иногда называют частичным порогом вариограммы, или коррелированной изменчивостью [16]. Следовательно, порог, или предел, вариограммы вычисляется как сумма дисперсии и эффекта самородка.
Вариограмма, ковариационные и корреляционные функции модели доступны через такие функции (методы) класса model модуля CovModel, как variogram, covariance и correlation (model.variogram, model.covariance и model.correlation) соответственно.
Каждая ковариационная модель определяется по меньшей мере шестью параметрами: размерностью dim, дисперсией var, масштабом флуктуации len_scale, величиной коэффициента масштабирования rescale, коэффициентом анизотропии anis и углами поворота angles, причем последние два зависят от размера. На рисунке 2 показаны: пример задания экспоненциальной модели (повторной реализации всего в трех строках) и результирующие функции модели, иллюстрирующие указанные параметры. В дополнение к предопределенным ковариационным моделям пользователи могут задавать свои собственные функции моделей в виде нормализованных корреляционных функций. В таблице 3 представлены ковариационные модели, предопределенные в GSTools.
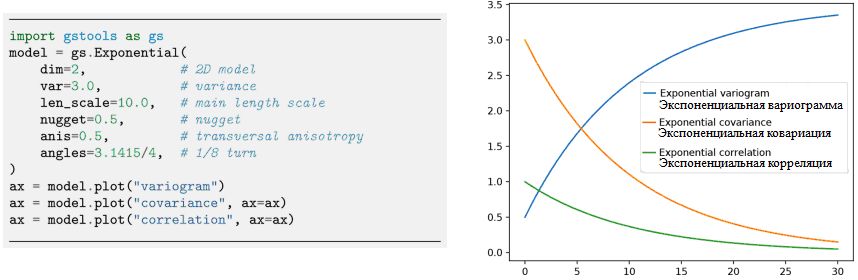
Рис. 2. Инициализация экспоненциальной ковариационной модели, заданной функцией cor(h)=exp(-h). Следует обратить внимание, что коэффициент масштабирования по умолчанию равен единице. На правом рисунке показаны кривые вариограммы, ковариационных и корреляционных функций модели, которые могут быть созданы с помощью удобных методов построения графиков [1, 16]
Таблица 3. Ковариационные модели, предопределенные в GSTools [1]

В дополнение к предопределенным ковариационным моделям пользователи могут задать свою собственную функцию модели, приведя нормализованную корреляционную функцию. На рисунке 3 показано задание экспоненциальной модели всего в трех строках.
![Рис. 3. Инициализация экспоненциальной ковариационной модели, определяемой пользователем. Единственное, что необходимо определить, – нормализованную корреляционную функцию cor [1]](/images/dynamic/img48046.jpg)
Зависящий от размера спектр изотропной ковариационной модели можно «вызвать» с помощью такой функции (метода) класса model модуля CovModel, как spectrum (model.spectrum). Этот спектр вычисляется непосредственно с использованием ковариационной функции следующим образом:
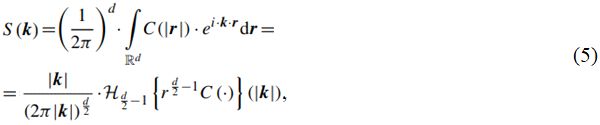
где r=|r| и k=|k| – нормы (модули, длина) соответствующих векторов; H – преобразование Ханкеля, которое обеспечивает математически автономную и численно надежную формулировку радиально-симметричного преобразования Фурье. В GSTools используется реализация H, предоставляемая hankel – библиотекой Python для выполнения простых и точных преобразований Ханкеля [56, 57]. Для улучшения вычислений в GSTools используются модели с известными аналитическими решениями.
Предпосылкой для кригинга или генерации случайного поля является то, что применяемая ковариационная функция является положительно определенной (положительно полуопределенной). Это можно проверить с помощью спектральной плотности, которая определяется следующим образом (здесь Мюллер и др. [1] обращают внимание на то, что спектр изотропной ковариационной модели S зависит только от нормы вектора k):
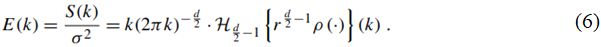
Из теоремы Бохнера [58] следует, что спектральная плотность является функцией плотности вероятности тогда и только тогда, когда лежащая в основе ковариационная функция является положительно определенной (положительно полуопределенной). Этому требованию удовлетворяют все предопределенные модели в GSTools. Как следствие, дисперсия ошибок при кригинге всегда неотрицательна.
Анизотропия и вращение
Мюллер и др. [1] отмечают, что вариограммы обычно определяются на основе лага r, что приводит к изотропной модели. Однако многие естественные процессы включают анизотропию с различными диапазонами корреляции в разных (ортогональных) направлениях. Примером может служить гидравлическая проводимость, где анизотропия обычно возникает из-за геологической стратификации. Реализация анизотропии в GSTools основана на безразмерном расстоянии h, определяемом формулой [16]:
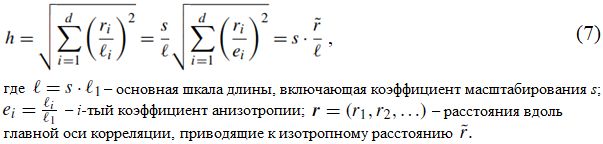
Следовательно, для полного описания анизотропной модели в GSTools используются: шкала основной длины, набор коэффициентов анизотропии и набор углов поворота.
На практике основные направления корреляции не обязательно следуют главной оси. CovModel учитывает вращение, используя углы поворота, число которых m зависит от размера d:

В двумерном случае вращение полностью описывается одним углом поворота в плоскости xy, а в трехмерном – тремя углами (в плоскостях xy, xz и yz). В трехмерном случае их часто называют углами Тейта – Брайана (Tait-Bryan) – углами рыскания (yaw), тангажа (pitch) и крена (roll) [59] (рис. 4). Пример трехмерного случая представлен на рисунке 5.
![Рис. 4. Наглядный пример изображения осей для определения углов Тейта – Брайана (углов рыскания, тангажа и крена) [60]](/images/dynamic/img48051.jpg)
![Рис. 5. Пространственная ковариационная структура анизотропной экспоненциальной модели в 3D, построенная с помощью встроенных (стандартных) интерактивных подпрограмм GSTools. В данном примере показан восьмой поворот в плоскости <i>xy</i> с коэффициентами анизотропии (1/2, 1/4). Углы поворота указаны в радианах [1]](/images/dynamic/img48052.jpg)
Одной из уникальных особенностей GSTools является поддержка произвольных размеров во всех предусмотренных процедурах. Для вращения с более высокой размерностью применяется следующая схема: первые углы совпадают с углами следующего более низкого измерения, а добавленные углы (d–1) описывают вращения в плоскостях добавленного измерения (в 3D – в плоскостях xz и yz). Таким образом, существует 6 углов поворота в 4D, 10 – в 5D и т. д. Вращение в более высоких измерениях имеет значение только для пространственно-временного моделирования с тремя пространственными измерениями и применяется в других областях научных исследований с использованием данных высокой размерности. Указанная схема была выбрана Мюллером и др. [1] для метрических пространственно-временных моделей для учета пространственной анизотропии аналогично тому, как это происходит для простой пространственной модели.
Вращение в плоскости xixj описывается следующей матрицей:
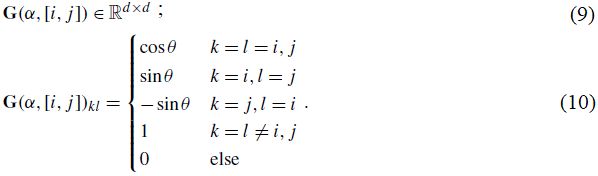
(else – это оператор «иначе», то есть оператор иного выбора (если не соблюдаются остальные условия, записанные выше строки с else в формуле (10)).
Порядок плоскостей вращения определяется описанной схемой, то есть I1=[1, 2] (плоскость xy), I2=[1, 3] (плоскость xz), I3=[2, 3] (плоскость yz) и т. д. Эти значения определяют матрицу вращения Rot для преобразования главных осей в направления корреляции и матрицу обратного вращения DeRot=Rot-1 для инверсии:
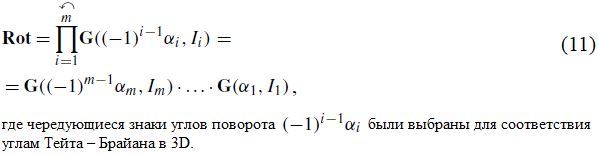
Для применения или исключения анизотропии используются матрица изотропии

и матрица анизотропии

Объединение этих двух типов матриц позволяет изотропно и анизотропно располагать пространственные точки с помощью следующих выражений:

GSTools имеет подпрограмму CovModel.isometrize для преобразования пространственных положений в их изотропные аналоги в соответствии с требованиями уравнения (7) и подпрограмму CovModel.anisometrize для выполнения следующих преобразований (инверсий) соответственно:

Географические координаты
Поверхность Земли, как отмечают Мюллер и др. [1], представляет собой неевклидово многообразие – и все крупномасштабные географически привязанные данные обязательно будут отражать это. Мы имеем дело с неевклидовой природой такого рода данных и при этом принимаем, что Земля представляет собой идеальную сферу и что расстояние между двумя точками p1=(φ1,λ1) и p2=(φ2,λ2) задается их широтой φ и долготой λ и может быть описано центральным углом, вычисленным по расстоянию по дуге большого круга:
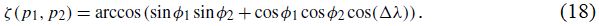
Из 3D моделей может быть получено огромное семейство достаточно достоверных моделей на сфере путем вставки хордальных расстояний, что дает в результате соответствующую ковариационную модель Ядренко CY [61]:

Лежащее в основе этого многообразие вводит новые ограничения для того, чтобы ковариационные модели были положительно определенными. Структура сферы допускает только изотропные модели. Но для мелкомасштабных применений допустимо принять анизотропию. Подходящей адаптацией является использование 2D проекции, подобной координатам Гаусса – Крюгера (Gauss-Kruger). В программном пакете GSTools для унифицированного представления для неевклидовых координат используются модели Ядренко, поскольку они облегчают использование всех представленных моделей с географическими координатами, как показано на рисунке 6.
![Рис. 6. Инициализация ковариационной модели Ядренко. Здесь в качестве коэффициента масштабирования используется радиус Земли, чтобы получить значимую шкалу длины. Работа в подпрограмме vario_yadrenko по-прежнему зависит от центрального угла, заданного в радианах [1]](/images/dynamic/img48061.jpg)
Эмпирическая вариограмма, подготовка данных и аппроксимация модели
Мюллер и др. [1] подчеркивают, что эмпирическая вариограмма является важным инструментом для анализа пространственно-коррелированных данных. Она оценивается с помощью субпакета stools.variogram, который предоставляет две оценочные функции для эмпирической вариограммы – Матерона (Matheron) и Кресси (Cressie) [47].
Оценочная функция Матерона γ для вариограммы пространственного случайного поля U по умолчанию задается следующим образом:
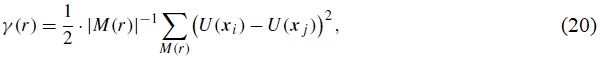
где M(r) – множество всех попарных точек пространственного случайного поля, разделенных расстоянием r c определенным допуском ε>0.
Оценочная функция Кресси, которая более устойчива к выбросам, задается так:
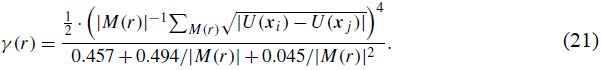
Для обеих оценок требуются предопределенные ячейки, или бины (структурные элементы разбиения массива данных на подмассивы, или подмножества) множества M(r) для группировки попарных расстояний между точками данного поля. GSTools предоставляет стандартную процедуру сортировки, где максимальная ширина такой ячейки устанавливается равной одной трети диаметра части пространства, содержащей поле, а количество ячеек определяется правилом Стёрджеса (Sturges) [62] и все они имеют одинаковую ширину. На рисунке 7 приведен пример оценки вариограммы неструктурированного пространственного случайного поля с автоматическим биннингом (разбиением множества значений на ячейки, или бины, то есть объединением соседних значений в ячейки).
![Рис. 7. Оценка эмпирической вариограммы модельных неструктурированных данных и подбор (аппроксимация) экспоненциальной модели. Было рассчитано, что количество ячеек (бинов, интервалов) составляет 21 при максимальном расстоянии между бинами (в общем интервале) около 45 [1]](/images/dynamic/img48064.jpg)
Мюллер и др. [1] отмечают, что GSTools учитывает анизотропию, предоставляя подпрограммы для оценки вариограмм вдоль заданных направлений с определенным допуском на угол и некой полосой пропускания. При использовании ортогональных осей можно подобрать («подогнать», аппроксимировать) теоретическую модель и ее коэффициенты анизотропии (рис. 8). Однако определение основных осей вращения по заданным данным зависит от пользователя и выходит за рамки представляемой здесь версии GSTools.
![Рис. 8. Оценка вариограмм по направлениям заданных основных осей. На фрагменте программы показана настройка для оценки и побора (аппроксимации) вариограммы к анизотропному полю. На графиках показаны основные оси поворотов модели и результаты подбора. Команды построения графиков опущены [1]](/images/dynamic/img48065.jpg)
Полевые данные часто не соответствуют нормальному распределению, которое является важным допущением для оценки вариограмм. Например, обычно принимается, что значения коэффициента фильтрации (водопроницаемости) распределены логнормально [63], в то время как данные о дождевых осадках нормализуются с помощью преобразования Бокса – Кокса (Box-Cox) [7]. Поэтому, как указывают Мюллер и др. [1], GSTools предоставляет следующий набор нормализаторов, основанных на степенных преобразованиях, которые могут быть адаптированы к заданному набору данных с использованием подхода максимального правдоподобия [64]: LogNormal (логнормальное преобразование), BoxCox (по Боксу – Коксу) [65], YeoJohnson (по Йео – Джонсону) [66], Modulus (по модулю) [67], Manly (по Манли) [68]. Пример их применения показан на рисунке 9. Сравнение всех предоставляемых в GSTools нормализаторов представлено на рисунке 10.
![Рис. 9. Оценка эмпирической вариограммы (график внизу слева) модельных неструктурированных данных (точечная диаграмма вверху слева) после нормализации входных значений методом Бокса – Кокса (Box-Cox). Справа показаны гистограммы данных до (вверху) и после (внизу) нормализации. В демонстрационных целях к эмпирической вариограмме была применена модель Матерна (Matern) [52]. Команды построения графиков опущены [1]](/images/dynamic/img48066.jpg)
![Рис. 10. Сравнение параметрических нормализаторов, предоставляемых в GSTools [1]](/images/dynamic/img48067.jpg)
Мюллер и др. [1] добавляют, что GSTools также предоставляет подпрограммы для удаления трендов (например, температура может уменьшаться с высотой, а гидравлическая проводимость может уменьшаться с глубиной) с помощью статистических методов. Еще одним приложением является анализ пространственной корреляции остатков после применения к данным регрессионной модели. Все подпрограммы, работающие с данными, имеют ключевые слова trend («тренд»), normalizer («нормализатор») и mean («среднее значение нормализованных данных»).
-
Во второй части статьи будут рассмотрены такие функциональные возможности пакета программ GSTools, как регрессионный анализ гауссовых процессов (кригинг), обработка, генерация и преобразование пространственных случайных полей и пространственно-временное моделирование зависящих от времени случайных процессов.
СПИСОК ЛИТЕРАТУРЫ (REFERENCES)
- Muller S., Schuler L., Zech A., Hesse F. GSTools v1.3: a toolbox for geostatistical modelling in Python. Geosci. Model Dev. 2022, 15: 3161–3182. doi.org/10.5194/gmd-15-3161-2022. URL: researchgate.net/publication/355409492_GSTools_v13_A_toolbox_for_geostatistical_modelling_in_Python.
- Krige D.G. A statistical approach to some basic mine valuation problems on the Witwatersrand. J. S. Afr. I. Min. Metall. 1951. 52: 119–139.
- Matheron G. Traite de geostatistique appliquee. Editions Technip, 962. 1. 333 .
- Hohn M.: Geostatistics and Petroleum Geology, computer methods in the geosciences, 2 edn. Springer Netherlands, 1999. doi.org/10.1007/978-94-011-4425-4.
- Kitanidis P. Introduction to Geostatistics: applications in Hydrogeology, 1st edn. Cambridge University Press, Cambridge, New York., 2008. ISBN 9780521587471.
- Goovaerts P. Geostatistics in soil science: state-of-the-art and perspectives. Geoderma. 1999. 89: 1–45. doi.org/10.1016/S0016-7061(98)00078-0.
- Cecinati F., Wani O., Rico-Ramirez M.A. Comparing approaches to deal with non-gaussianity of rainfall data in kriging-based radar-gauge rainfall merging. Water Resour. Res. 2017. 53: 8999–9018. doi.org/10.1002/2016WR020330.
- Rossi R.E., Mulla D.J., Journel A.G., Franz E.H. Geostatistical tools for modeling and interpreting ecological spatial dependence. Ecol. Monogr. 1992. 62: 277–314. doi.org/10.2307/2937096.
- Sales M.H., Souza C.M., Kyriakidis P.C., Roberts D.A., Vidal E. Improving spatial distribution estimation of forest biomass with geostatistics: a case study for Rondonia, Brazil. Ecol. Model. 2007. 205: 221–230. doi.org/10.1016/j.ecolmodel.2007.02.033.
- Monestiez P., Petrenko A., Leredde Y., Ongari B. Geostatistical analysis of three dimensional current patterns in coastal oceanography: application to the gulf of lions (NW Mediterranean sea). In: geoENV IV – Geostatistics for environmental applications, edited by: Sanchez-Vila X., Carrera J., GomezHernandez J.J. Springer Netherlands, Dordrecht, 2004. 367–378. doi.org/10.1007/1-4020-2115-1_31.
- Schuler L.. Muller, S. GeoStat – examples/gstoolsherten-example: v1.0. Zenodo. 2021. doi.org/10.5281/zenodo.5159658.
- Kaputin Yu.E., Ezhov A.I., Henli S. Geostatistika v gorno-geologicheskoy praktike [Geostatistics in mining-and-geological practice]. 1995. 165 s. Apatity: KNTs RAN, 1995. 188 s. (in Russian) (Капутин Ю.Е., Ежов А.И., Хенли С. Геостатистика в горно-геологической практике. 1995. 165 с. Апатиты: КНЦ РАН, 1995. 188 с.).
- Porotov G.S. Matematicheskiye metody modelirovaniya v geologii: uchebnik [Mathematical methods of modeling in Geology: a textbook]. SPb.: Sankt-Peterburgskiy gosudarstvenniy gorniy institut (tekhnicheskiy universitet), 2006. 223 s. (in Russian) (Поротов Г.С. Математические методы моделирования в геологии: учебник. СПб.: Санкт-Петербургский государственный горный институт (технический университет), 2006. 223 с.).
- Demyanov V.V., Savelyeva E.A. Geostatistika: teoriya i praktika [Geostatistics: theory and practice] / pod red. R.V. Arutyunyana. M.: Nauka, 2010. 327 s. (in Russian) (Демьянов В.В., Савельева Е.А. Геостатистика: теория и практика / под ред. Р.В. Арутюняна. М.: Наука, 2010. 327 с.).
- Pyrcz M.J., Deutsch C.V. Geostatistical reservoir modeling, 2 edn. Oxford University Press, Oxford, 2014. ISBN 978-0199731442.
- Rubin Y. Applied Stochastic Hydrogeology, 1st edn. Oxford University Press, New York, 2003. ISBN 9780195138047. doi.org/10.1093/oso/9780195138047.001.0001.
- Diggle P., Ribeiro P.J. Model-based Geostatistics, Springer Series in Statistics, 1st edn. Springer-Verlag, New York, 2007. doi.org/10.1007/978-0-387-48536-2.
- Banerjee S., Carlin B.P., Gelfand A.E. Hierarchical modeling and analysis for spatial data, 2 edn. Chapman and Hall/CRC, Boca Raton, 2014. doi.org/10.1201/b17115.
- Zhang Y.-K., Zhang D. Forum: the state of Stochastic Hydrology. Stoch. Env. Res. Risk A. 2004. 18: 265. doi.org/10.1007/s00477-004-0190-8.
- Rajaram H. Debates – Stochastic Subsurface Hydrology from theory to practice: Introduction. Water Resour. Res. 2016. 52: 9215–9217. doi.org/10.1002/2016WR020066.
- Neuman S.P. Stochastic groundwater models in practice. Stoch. Env. Res. Risk A. 2004. 18: 268–270. doi.org/10.1007/s00477-004-0192-6.
- Winter C.L.: Stochastic Hydrology: practical alternatives exist. Stoch. Env. Res. Risk A. 2004. 18: 271–273. doi.org/10.1007/s00477-004-0198-0.
- Cirpka O.A., Valocchi A.J. Debates – Stochastic Subsurface Hydrology from theory to practice: does stochastic subsurface hydrology help solving practical problems of contaminant hydrogeology? Water Resour. Res. 2016. 52: 9218–9227. doi.org/10.1002/2016WR019087.
- Fiori A., Cvetkovic V., Dagan G., Attinger S., Bellin A., Dietrich P., Zech A., Teutsch G. Debates – Stochastic Subsurface Hydrology from theory to practice: The relevance of stochastic subsurface hydrology to practical problems of contaminant transport and remediation. What is characterization and stochastic theory good for? Water Resour. Res. 2016. 52: 9228–9234. doi.org/10.1002/2015WR017525.
- Bellin A., Rubin Y. HYDRO_GEN: a spatially distributed random field generator for correlated properties. Stoch. Hydrol. Hydraul. 1996. 10: 253–278. doi.org/10.1007/BF01581869,
- Deutsch C.V., Journel A.G.: GSLIB: geostatistical software library and user’s guide, Applied geostatistics series, 2. edn. Oxford University Press, 1997. ISBN 9780195100150.
- Brouste A., Istas J., Lambert-Lacroix S. On fractional Gaussian random fields simulations. J. Stat. Softw. 2008. 23: 1–23. doi.org/10.18637/jss.v023.i01.
- Rubin Y., Chen X., Murakami H., Hahn M. A Bayesian approach for inverse modeling, data assimilation, and conditional simulation of spatial random fields. Water Resour. Res. 2010. 46: W10523. doi.org/10.1029/2009WR008799.
- Pebesma E.J. Multivariable geostatistics in S: the gstat package. Comput. Geosci. 2004. 30: 683–691. doi.org/10.1016/j.cageo.2004.03.012.
- Savoy H., Hesse F., Rubin Y.: anchoredDistr: a package for the Bayesian inversion of geostatistical parameters with multi-type and multi-scale data. R Journal. 2017. 9: 6–17. doi.org/10.32614/RJ-2017-034.
- Hesse F., Prykhodko V., Schluter S., Attinger S.: Generating random fields with a truncated power-law variogram: a comprarison of several numerical methods. Environ. Modell. Softw. 2014. 55: 32–48. doi.org/10.1016/j.envsoft.2014.01.013.
- Vrugt J.A. Markov chain Monte Carlo simulation using the DREAM software package: Theory, concepts, and MATLAB implementation. Environ. Modell. Softw. 2016. 75: 273–316. doi.org/10.1016/j.envsoft.2015.08.013.
- Rubin Y., Chang C.-F., Chen J., Cucchi K., Harken B., Hesse F., Savoy H. Stochastic hydrogeology’s biggest hurdles analyzed and its big blind spot. Hydrol. Earth Syst. Sci. 2018. 22: 5675–5695. doi.org/10.5194/hess-22-5675-2018.
- Muller S., Schuler L. GeoStat – framework/GSTools: v1.3.5 “Pure Pink”. Zenodo. January 20, 2022. doi.org/10.5281/zenodo.5883346.
- Embarak O. Data analysis and visualization using Python analyze data to create visualizations for BI systems, 1st edn. Apress, 2018, 394 р.
- Rossum G., Dreyk F.L.Dzh., Otkidach D.S., i dr. Yazyk programmirovaniya Python [Python programming language]. 2001, 454 c. URL: script-coding.com/Python/Otkidach.html (Россум, Г., Ф.Л.Дж. Дрейк, Д.С. Откидач и др. Язык программирования Python. 2001, 454 c. URL: script-coding.com/Python/Otkidach.html).
- Beazley D. Python. Essential Reference, 4th edn. Addison-Wesley, 2010. 860 p. (Бизли Д. Python. Подробный справочник (4-е издание). СПб.: Символ-Плюс, 2010. 864 с. (пер. с англ.)).
- Buynachev S.K., Boklag N.Yu. Osnovy programmirovaniya na yazyke Python: uchebnoye posobiye [Basics of programming in Python: a tutorial]. Ekaterinburg: Izd-vo Ural'skogo un-ta, 2014. 91 c. (Буйначев С.К., Боклаг Н.Ю. Основы программирования на языке Python: учебное пособие. Екатеринбург: Изд-во Уральского ун-та, 2014. 91 c.).
- Kovalevskiy E. Geological modelling on the base of Geostatistics. EAGE Student Lecture Tour (SLT), 2011–2012. URL: petroportal.ru/uploads/library/10_4b6fc13e7ef16f780697332a41680c31.pdf (in Russian) (Ковалевский Е. Геологическое моделирование на основе геостатистики. Студенческое лекционное турне EAGE, 2011–2012. URL: petroportal.ru/uploads/library/10_4b6fc13e7ef16f780697332a41680c31.pdf.)
- Uzielli M., Lacasse S., Nadim F., Phoon K.K. Soil variability analysis for geotechnical practice. Proceedings of the 2nd international workshop on characterisation and engineering properties of natural soils. Singapore, 2006.
- Isaaks E.H., Srivastava R.M. An Introduction to Applied Geostatistics. Oxford University Press, Inc. New York, 1989. 561 p.
- Yan-lin S., Ai-ling Z.A., You-bin H., Ke-yan X. 3D geological modeling and its application under complex geological conditions. Procedia Engineering. 2011. 12: 41–46.
- Kanevskiy M.F., Demyanov V.V., Savelyeva E.A., Chernov S.Yu., Timonin V.A. Elementarnoye vvedeniye v geostatistiku. Problemy okruzhayushchey sredy i prirodnyh resursov. Moskva, VINITI, 1999. 11 (in Russian) (Каневский М.Ф., Демьянов В.В., Савельева Е.А., Чернов С.Ю., Тимонин В.А. Элементарное введение в геостатистику // Проблемы окружающей среды и природных ресурсов. 1999. Москва: ВИНИТИ, 1999. № 11).
- Bohling G. Introduction to geostatistics and variogram analysis. Kansas Geological Survey, 2005, 1: 1–20.
- Armstrong M. Geostatistics (in 2 volumes). Kluwer Academic Publishers, 1989. 1027 p.
- Phoon K.K., Kulhawy F.H. Characterization of geotechnical variability. Canadian Geotechnical Journal. 1999. 36: 612–624.
- Webster R., Oliver M.A. Geostatistics for environmental scientists, 2d edn. John Wiley & Sons, 2007. ISBN 978-0-470-02858-2.
- Di Federico V., Neuman S.P. Scaling of random fields by means of truncated power variograms and associated spectra. Water Resour. Res. 1997. 33: 1075–1085. doi.org/10.1029/97WR00299.
- Wackernagel H. Multivariate Geostatistics: an introduction with applications, 3-d edn. Springer-Verlag, Berlin Heidelberg, 2003. ISBN 978-3-540-44142-7. doi.org/10.1007/978-3-662-05294-5.
- Rasmussen C.E., Williams C.K. I. Gaussian processes for machine learning, 1st edn. The MIT Press, 2005. ISBN 9780262256834. doi.org/10.7551/mitpress/3206.001.0001.
- Chiles J.-P., Delfiner P. Geostatistics: modeling spatial uncertainty, 2d edn. Wiley Series in Probability and Statistics (edited by Balding D.J., et al.). John Wiley & Sons, 2012. doi.org/10.1002/9781118136188.
- Matern B. Spatial variation – stochastic models and their applications to some problems in forest survey sampling investigations. Reports of the Forest Research Institute of Sweden. 1960. 49: 1–144.
- Wendland H. Piecewise polynomial, positive definite and compactly supported radial functions of minimal degree. Adv. Comput. Math. 1995. 4: 389–396. doi.org/10.1007/BF02123482.
- Muller S., Hesse F., Attinger S., Zech A. The extended generalized radial flow model and effective conductivity for truncated power law variograms. Adv. Water Resour. 2021. 156: 104027. doi.org/10.1016/j.advwatres.2021.104027, 2021a.
- Abramowitz M., Stegun I.A. Handbook of mathematical functions, 10th edn. Dover Publications, New York, 1972. ISBN 978-0-486-61272-0.
- Murray S.G., Poulin F.J.: hankel: a Python library for performing simple and accurate Hankel transformations, The Journal of Open Source Software. 2019. 4: 1397. doi.org/10.21105/joss.01397,
- Ogata H. A numerical integration formula based on the Bessel functions. Publ. Res I. Math. Sci. 2005. 41: 949–970. doi.org/10.2977/prims/1145474602.
- Rudin W. Fourier analysis on groups, 1st edn. WileyInterscience, John Wiley & Sons, 1990. ISBN 9780470744819. doi.org/10.1002/9781118165621.
- Goldstein H. Classical mechanics, 2nd edn. Addison-Wesley, 1980. 672 p. ISBN 9780201029185.
- Fiori S. A closed-form expression of the instantaneous rotational lurch index to evaluate its numerical approximation. Symmetry. 2019. 11 (10): 1208. doi.org/10.3390/sym11101208.
- Lantuejoul C., Freulon X., Renard D. Spectral simulation of isotropic Gaussian random fields on a sphere. Math. Geosci. 2019. 51: 999–1020. doi.org/10.1007/s11004-019-09799-4.
- Sturges H.A. The choice of a class interval. J. Am. Stat. Assoc. 1926. 21: 65–66. doi.org/10.1080/01621459.1926.10502161.
- Dagan G. Flow and transport in porous formations, 1st edn. Springer, Berlin, Heidelberg, 1989. doi.org/10.1007/978-3-642-75015-1.
- Eliason S.R.: Maximum likelihood estimation: Logic and practice, 1st edn. Sage Publications. Thousand Oaks, CA, US, 1993. ISBN 9781506315904.
- Box G.E.P., Cox D.R. An analysis of transformations. J. Roy. Stat. Soc B. 1964. 26: 211–243. doi.org/10.1111/j.2517-6161.1964.tb00553.x.
- Yeo I., Johnson R.A. A new family of power transformations to improve normality or symmetry. Biometrika. 2000. 87: 954–959. doi.org/10.1093/biomet/87.4.954.
- John J.A., Draper N.R. An alternative family of transformations. J. Roy. Stat. Soc. C-App. 1980. 29: 190–197. doi.org/10.2307/2986305.
- Manly B.F.J. Exponential data transformations. J. Roy. Stat. Soc. D-Sta. 1976. 25: 37–42. doi.org/10.2307/2988129.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц




















