О новом методе анализа надежности откосов и склонов без преобразований существующих программ

ВВЕДЕНИЕ

Как указывают Цзян с соавторами [1], в последние годы пространственная изменчивость свойств грунтов привлекает широкое внимание при анализе устойчивости откосов и склонов. Но в большинстве исследований, выполненных до публикации статьи [1], проводился детерминированный анализ устойчивости откосов или склонов с использованием традиционного метода предельного равновесия (МПР). Затем для анализа надежности откоса или склона с учетом пространственно изменчивых свойств грунта МПР комбинировался с теорией случайных полей. После этого для оценки вероятности разрушения использовалось моделирование методом Монте-Карло.

Однако, как отмечают Цзян и др. [1], потенциальная проблема использования метода предельного равновесия заключается в том, что должны быть приняты некоторые допущения, касающиеся формы поверхности скольжения или механизма потери устойчивости. Кроме того, в этом случае не учитывается напряженно-деформированное поведение грунта, а также невозможен реалистичный учет пространственной изменчивости его свойств, если форма поверхности скольжения в разрезе не является круглой. Но метод конечных элементов (МКЭ) позволяет преодолеть отмеченные недостатки МПР.

Что касается оценки надежности откосов и склонов, то хотя моделирование методом Монте-Карло и подходит для оценки вероятности разрушения при пространственной изменчивости параметров прочности на сдвиг, необходимые для него время и ресурсы могут быть неприемлемыми, поскольку для достаточно точной оценки в этом случае необходимо значительное количество «прогонов» конечноэлементной модели. Особенно много усилий затрачивается при анализе с относительно небольшим уровнем вероятности разрушения или когда при расчете устойчивости требуется выполнить сложный анализ с помощью МКЭ.

Традиционные стохастические (вероятностные) конечноэлементные методы требуют значительной модификации существующих компьютерных программ, предназначенных для детерминированного анализа на основе МКЭ, что почти невозможно для большинства инженеров, не имеющих доступа к исходным кодам коммерческих программных пакетов.

Поэтому необходимо более эффективно исследовать те методы анализа надежности откосов и склонов, которые учитывают пространственно изменчивые параметры прочности на сдвиг и требуют сложного анализа методом конечных элементов для определения коэффициента запаса устойчивости.

Ввиду вышесказанного Цзян с коллегами [1] предлагают для анализа надежности откосов и склонов с учетом изменчивых параметров прочности на сдвиг использовать стохастический метод конечных элементов, являющийся неинтрузивным (то есть не требующим доступа к исходным кодам и внесения изменений в существующие конечноэлементные программы).

МОДЕЛИРОВАНИЕ СЛУЧАЙНЫХ ПОЛЕЙ СВОЙСТВ ГРУНТОВ

Пространственная изменчивость свойств грунтового массива

Гауссовское случайное поле полностью определяется средним значением µ(x), стандартным отклонением σ(x) и автокорреляционной функций ρ(x₁, x₂). Последняя является важной физической величиной для описания пространственной корреляции свойств грунта.

Цзян и др. [1] используют следующую двумерную квадратичную экспоненциальную автокорреляционную функцию с разными автокорреляционными интервалами в горизонтальном и вертикальном направлениях:

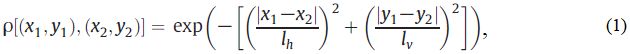
где (x₁, y₁), (x₂, y₂) – координаты двух произвольных точек в двумерном пространстве; l_h, l_v – интервалы автокорреляции в горизонтальном и вертикальном направлениях соответственно.

Разложение Карунена – Лоэва

Цзян и др. [1] напоминают, что для дискретизации случайного поля можно использовать несколько методов, таких как метод средней точки, метод разбиения на локальные средние, метод функции формы, разложение Карунена – Лоэва (Karhunen-Loeve). Поскольку последний из перечисленных методов требует минимального количества случайных переменных для заданного уровня точности, он используется для дискретизации двумерных анизотропных случайных полей параметров прочности на сдвиг.

Далее авторы статьи [1], чтобы облегчить понимание предлагаемого метода, кратко рассматривают разложение Карунена – Лоэва.

Случайное поле H(x, θ) представляет собой набор случайных величин, связанных с непрерывным показателем

где Ω – открытое множество величин Rⁿ, описывающее геометрию системы; θ – координата в пространстве исходов, то есть:

Дискретизация случайного поля с использованием разложения Карунена – Лоэва основана на спектральном разложении его автокорреляционной функции ρ(x₁, x₂), которая обычно является ограниченной, симметричной и положительно определенной. Следовательно, дискретизация случайного поля является задачей на определение собственных значений однородного интегрального уравнения Фредгольма следующего вида:

где x₁, x₂ – координаты двух точек; f_i, λ_i – соответственно собственные функции и собственные значения одномерной автокорреляционной функции ρ(x₁, x₂).

Тогда собственные моды сепарабельной (разделимой) многомерной автокорреляционной функции вычисляются путем умножения на собственные моды, полученные из уравнения (4).

Задача нахождения собственных значений интегрального уравнения Фредгольма (4) часто решается численно из-за ее сложности. Авторы работы [1] решили применить метод Галеркина (с использованием гармонических вейвлетов).

Разложение в ряд двумерного случайного поля H_i(x, y) выражается так:

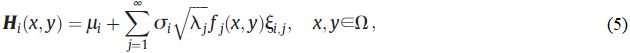
где ξ_i,j – ортогональные случайные коэффициенты (некоррелированные случайные переменные с нулевым средним и единичной дисперсией).

Разложение в ряд (5), называемое разложением Карунена – Лоэва, характеризует момент второго порядка с точки зрения некоррелированных случайных переменных и детерминированных ортогональных функций. Известно, что оно сходится в смысле среднеквадратического отклонения для любого распределения H_i(x, y).

На практике используется приближение в виде ряда с конечным количеством членов в уравнении (5), то есть:

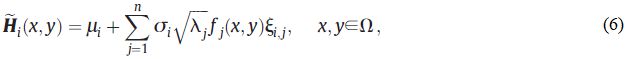
где n – количество сохраняемых членов разложения Карунена – Лоэва, которое сильно зависит от желаемой точности и автокорреляционной функции случайного поля (малые значения автокорреляционных интервалов приведут к значительному увеличению числа собственных мод n).

В некоторых исследованиях в качестве меры точности усеченного ряда использовался параметр ε, который определяется следующим образом:

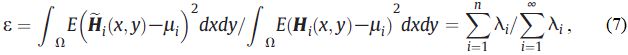
где собственные значения λ_i отсортированы по убыванию.

Большое значение параметра точности ε всегда свидетельствует о высокой точности усеченного ряда.

Взаимно коррелированные негауссовские случайные поля

Далее Цзян с коллегами [1] рассказывают о том, что в инженерно-геологической практике часто приходится моделировать более одного геотехнического параметра с помощью случайных полей. Кроме того, геотехническая литература изобилует информацией о взаимных корреляциях между двумя геотехническими параметрами. В таких случаях требуется обработка взаимно коррелированных случайных полей.

Принимается, что все поля, моделируемые в области Ω, имеют одинаковую автокорреляционную функцию, а структура взаимной корреляции между каждой парой смоделированных полей определяется коэффициентом взаимной корреляции. Это может обеспечить соответствие целевых случайных полей структуре корреляции в пределах каждого поля.

При указанных допущениях модальное разложение автокорреляционной функции выполняется только один раз. Для разложения взаимно коррелированных случайных полей может применяться один и тот же спектр собственных функций и собственных значений. Здесь Цзян и др. [1] отмечают, что используемые наборы случайных величин для разложения взаимно коррелированных случайных полей также являются взаимно коррелированными.

Далее авторы статьи [1] иллюстрируют процедуру моделирования взаимно коррелированных случайных полей на примере удельного сцепления c и угла внутреннего трения ϕ, обозначив матрицу коэффициентов взаимной корреляции между c и ϕ следующим образом:

Сначала формируется матрица выборок ξ размером (n х N_F) х N_p, где N_p – количество смоделированных выборок (или количество «прогонов» детерминированной модели устойчивости откоса или склона), N_F – количество случайных полей. Каждый из N_p столбцов является одной реализацией вектора независимой стандартной нормальной выборки, разбитого на N_F векторов, каждый из которых имеет размер n.

Для дискретизации взаимно коррелированных случайных полей с участием двух пространственных переменных c и ϕ можно сформировать k-й столбец матрицы выборок ξ

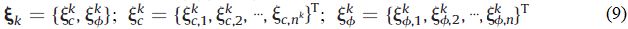
с помощью двух наборов точек независимых стандартных нормальных распределений вероятностей или точек выборки латинского гиперкуба.

Нижняя треугольная матрица L размером 2 х 2 получается с помощью разложения Холецкого матрицы коэффициентов взаимной корреляции R_c,ф. Затем получается матрица коррелированной стандартной нормальной выборки χ, k-й столбец которой χ_k определяется формулой:

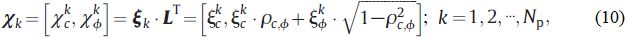
где матрица ξ_k размером n х 2 формируется путем перестройки k-го столбца матрицы выборок ξ.

Если принять в качестве основы вектор коррелированной стандартной нормальной выборки χ_k, то k-я реализация каждого из взаимно коррелированных гауссовских случайных полей c и ϕ запишется так:

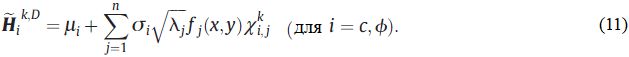
Подобно изовероятностному преобразованию ненормально распределенных случайных величин, k-я реализация аппроксимации (приближения) взаимно коррелированных негауссовских случайных полей может быть получена покомпонентно:

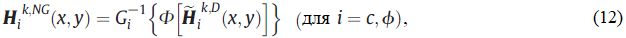
где G_i^-1 – обратная функция предельного кумулятивного распределения каждой компоненты негауссовского векторного случайного поля H^NG(x, y); Ф – функция стандартного распределения Гаусса.

Если параметры прочности на сдвиг (c, ϕ) считаются распределенными логнормально, то k-я реализация приближенных взаимно коррелированных логнормальных случайных полей может быть получена путем потенцирования приближенных взаимно коррелированных гауссовских случайных полей из уравнения (12) следующим образом:

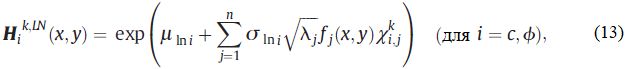
где

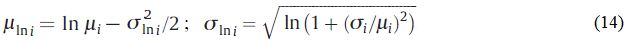
представляют собой среднее значение и стандартное отклонение гауссовской случайной величины ln i соответственно.

ПРОЦЕДУРА ИСПОЛЬЗОВАНИЯ НЕИНТРУЗИВНОГО СТОХАСТИЧЕСКОГО МЕТОДА КОНЕЧНЫХ ЭЛЕМЕНТОВ

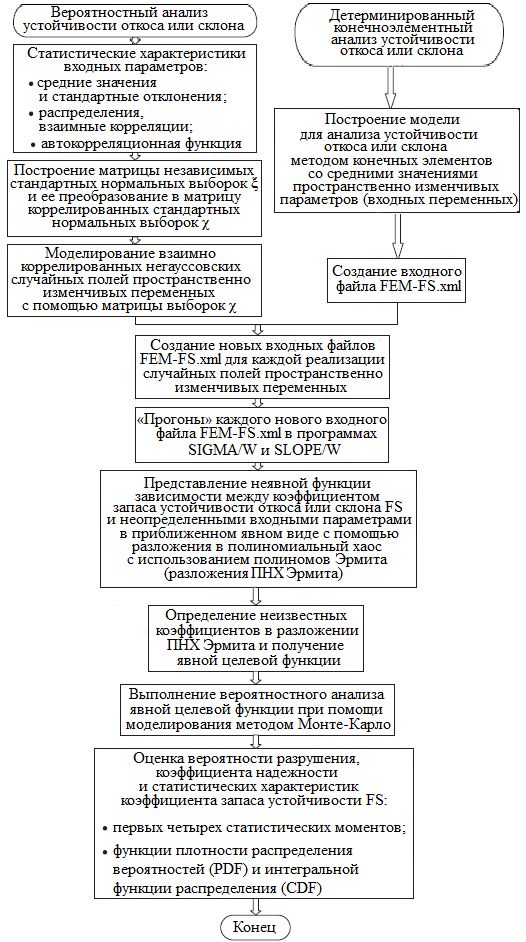
Цзян с соавторами [1] описывают следующие девять шагов, из которых состоит процедура выполнения анализа надежности откоса или склона с помощью неинтрузивного стохастического метода конечных элементов (см. также рисунок).

1. Определение пространственно изменчивых переменных и их статистических показателей (средних значений, коэффициентов вариации COV, распределений и коэффициентов взаимной корреляции между переменными, связанными с задачей оценки надежности откоса или склона). Далее – выбор подходящей автокорреляционной функции и оценка автокорреляционных интервалов в горизонтальном и вертикальном направлениях для двумерной модели случайного поля.

2. Построение модели для анализа устойчивости откоса или склона методом конечных элементов со средними значениями входных переменных с использованием программ SIGMA/W и SLOPE/W (GEO-SLOPE International Ltd., 2010 a, b). Далее – нахождение координат (x_o,i, y_o,i) центроида (геометрического центра) i-го элемента, где i = 1, 2, ..., n_e; n_e – количество конечных элементов. Затем – сохранение файла детерминированной модели устойчивости откоса или склона как входного с именем FEM-FS.xml. В этом файле содержится вся информация, нужная для программ SIGMA/W и SLOPE/W (она также может быть введена непосредственно через текстовый редактор). Цзян и др. [1] обращают внимание читателей на то, что коэффициент запаса устойчивости склона рассчитывается с использованием метода конечных элементов (Farias, Naylor, 1998) в SLOPE/W с использованием поля напряжений, полученного методом конечных элементов в SIGMA/W.

3. Построение матрицы независимых стандартных нормальных выборок ξ размером (n х N_F) х N_p с использованием вероятностных коллокационных точек (или точек выборки латинского гиперкуба). Далее – преобразование матрицы независимых стандартных нормальных выборок ξ в матрицу коррелированных стандартных нормальных выборок χ с помощью уравнения (10).

4. Моделирование взаимно коррелированных негауссовских случайных полей пространственно изменчивых переменных с помощью матрицы выборок χ, координат (x_o,i, y_o,i) и разложения Карунена – Лоэва. Таким образом – получение N_p реализаций взаимно коррелированных негауссовых случайных полей пространственно изменчивых значений параметров прочности на сдвиг в физическом пространстве, которые присваиваются каждому конечному элементу рассматриваемого откоса или склона.

5. Замена средних значений соответствующих неопределенных входных параметров в центроиде (геометрическом центре) каждого конечного элемента в файле FEMFS.xml, созданном на шаге 2, на каждую пару пространственно изменчивых переменных (то есть c и ϕ) в каждой реализации случайных полей из шага (4). Таким образом – создание N_p различных новых входных файлов FEM-FS.xml. При этом не требуется усилий по программированию для модификации существующей конечноэлементной программы в отличие от процедуры использования спектрального стохастического метода конечных элементов (Ghanem, Spanos, 2003).

6. «Прогоны» каждого нового входного файла FEM-FS.xml, созданного на шаге (5), в программах SIGMA/W и SLOPE/W для детерминированного конечноэлементного анализа устойчивости откоса или склона. Это может выполняться автоматически с помощью Winbatch™ (скриптового языка Microsoft Windows, имеющего дополнительный компилятор, используемый для создания автономно выполняемых программ). Этот процесс приведет к получению N_p различных коэффициентов запаса устойчивости откоса или склона FS = (FS₁, FS₂, ..., FS_Np), которые можно будет непосредственно «извлечь» из соответствующих файлов результатов FEM-FS.fac.

7. Замена неявной функции зависимости между коэффициентом запаса устойчивости откоса или склона FS и неопределенными входными параметрами на разложение в полиномиальный хаос (разложение ПНХ) с использованием полиномов Эрмита (такое разложение для конечноэлементного анализа откоса или склона называется метамоделью, суррогатной моделью, моделью модели, разложением ПНХ Эрмита (Isukapalli et al., 1998; Ghanem, Spanos, 2003)):

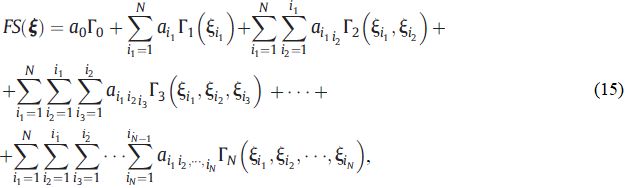
где N – общее количество случайных величин, N = n х N_F; a (с разными нижними индексами) – неизвестные коэффициенты, подлежащие оценке (количество этих коэффициентов в уравнении равно N_c = (N + p)!/(N! х p!) для разложения ПНХ p-го порядка); ξ_i (с разными нижними индексами после i) – вектор независимых стандартных нормальных переменных, представляющих неопределенности во входных параметрах, который соответствует случайным переменным, используемым для дискретизации случайных полей с применением разложения Карунена – Лоэва (5); Г_N(ξ_i1, ξ_i12, ..., ξ_iN), – многомерные многочлены Эрмита N-й степени.

Такое разложение широко используется в геотехнике (Li et al., 2011; Mollon et al., 2011; Al-Bittar, Soubra, 2013). Для получения подробной информации Цзян с соавторами [1] советуют ознакомиться с работами Ганема и Спаноса (Ghanem, Spanos, 2003), Ли и др. (Li et al., 2011).

8. Определение неизвестных коэффициентов в разложении ПНХ Эрмита путем приравнивания коэффициентов запаса устойчивости, полученных на шаге 6, к оценкам по уравнению (15) при матрице ξ из шага 3. Далее – формирование и решение системы линейных уравнений. Для этой цели могут быть использованы коллокационный метод, основанный на принципе линейной независимости (Li, Zhang, 2007), или регрессия, основанная на подходе Исукапалли и др. (Isukapalli et al., 1998). В результате – нахождение явной функции зависимости между FS и неопределенными входными параметрами.

9. Выполнение вероятностного анализа явной целевой функции G(ξ) = (FS(ξ) – 1). Вероятность разрушения и соответствующий коэффициент запаса устойчивости FS можно оценить с помощью моделирования методом Монте-Карло с использованием 1 млн выборок для целевой функции с коэффициентом FS, представленным разложением ПНХ Эрмита. Первые четыре статистических момента также могут быть непосредственно оценены с помощью разложения ПНХ (Mollon et al., 2011). Здесь Цзян и др. [1] отмечают, что оценка целевой функции не требует опять детерминированного конечноэлементного анализа устойчивости откоса или склона, а включает только расчеты по простым алгебраическим выражениям, что намного эффективнее в вычислительном отношении.

Рис. Блок-схема процедуры выполнения анализа надежности откосов или склонов с помощью неинтрузивного стохастического метода конечных элементов

ВЫВОДЫ, СДЕЛАННЫЕ АВТОРАМИ СТАТЬИ [1]

Авторы статьи [1] предложили метод анализа надежности откосов и склонов с учетом пространственно изменчивых параметров прочности на сдвиг с помощью неинтрузивного стохастического метода конечных элементов (прежде всего они использовали разложение Карунена – Лоэва для дискретизации двумерных взаимно коррелированных негауссовских случайных полей этих пространственно изменчивых переменных). Кроме того, они рассмотрели конкретные примеры использования этого метода, которые продемонстрировали его возможности и достоверность получаемых результатов (но в настоящем обзоре эти примеры не представлены).

В заключение Цзян с коллегами [1] делают следующие выводы (в том числе на основе рассмотренных ими конкретных случаев анализа).

1. Предложенный неинтрузивный стохастический метод конечных элементов представляет собой практический инструмент для решения задач по определению надежности откосов и склонов с учетом пространственной изменчивости параметров прочности на сдвиг, и он не требует от пользователей изменений в программах, предназначенных для детерминированного конечноэлементного анализа, и доступа к их исходным кодам. Более того, при его использовании детерминированный конечноэлементный анализ и вероятностный анализ разделены.

2. Этот метод позволяет эффективно оценивать надежность откосов или склонов при наличии пространственной изменчивости параметров прочности на сдвиг. С его помощью можно существенно уменьшить количество обращений к детерминированной конечноэлементной модели и гораздо более эффективно оценить надежность откоса или склона с учетом изменчивых параметров сдвиговой прочности, чем с применением метода выборки значений из латинского гиперкуба, в том числе при больших значениях коэффициента устойчивости (что соответствует большинству практических случаев).

3. Если коэффициент вариации показателей прочности на сдвиг превышает критическое значение или если коэффициент запаса устойчивости FS относительно невелик, то игнорирование пространственной изменчивости параметров сдвиговой прочности приведет к оценкам вероятности разрушения откоса или склона, не обеспечивающим запаса устойчивости. При этом критические значения коэффициента вариации параметров прочности на сдвиг увеличиваются с ростом коэффициента FS.

4. Изменение вероятности разрушения откоса или склона сильно зависит от коэффициента запаса устойчивости FS. Чем меньше значение FS, тем больше вероятность того, что параметры прочности на сдвиг с низкой изменчивостью будут приводить к завышению вероятности разрушения.

5. Когда пространственная автокорреляция параметров прочности на сдвиг очень слаба, для получения достаточно точных результатов оценки надежности требуется больше членов разложения Карунена – Лоэва. Чтобы повысить эффективность вычислений, в неинтрузивный стохастический метод конечных элементов должны быть включены другие высокоэффективные разложения ряда, например в разреженный полиномиальный хаос.

ИСТОЧНИК

1. Jiang S.H., Li D.Q., Zhang L.M., Zhou C.B. Slope reliability analysis considering spatially variable shear strength parameters using a non-intrusive stochastic finite element method // Engineering Geology. 2014. Vol. 168. P. 120–128.

СПИСОК ПУБЛИКАЦИЙ, НА КОТОРЫЕ ССЫЛАЮТСЯ АВТОРЫ СТАТЬИ [1]

Al-Bittar T., Soubra A.-H. Bearing capacity of strip footings on spatially random soils using sparse polynomial chaos expansion // Int. J. Numer. Anal. Methods Geomech. 2013. Vol. 37. № 13. P. 2039–2060.

Ching J., Phoon K.K. Effect of element sizes in random field finite element simulations of soil shear strength // Comput. Struct. 2013. Vol. 126. P. 120–134.

Cho S.E. Effects of spatial variability of soil properties on slope stability // Eng. Geol. 2007. Vol. 92. № 3–4. P. 97–109.

Cho S.E. Probabilistic assessment of slope stability that considers the spatial variability of soil properties // J. Geotech. Geoenviron. 2010. Vol. 136. № 7. P. 975–984.

Cho S.E. Probabilistic analysis of seepage that considers the spatial variability of permeability for an embankment on soil foundation // Eng. Geol. 2012. Vol. 133–134. P. 30–39.

Choi S.K., Canfield R., Grandhi R., Pettit C. Polynomial chaos expansion with Latin hypercube sampling for estimating response variability // AIAA J. 2004. Vol. 42. № 6. P. 1191–1198.

Der Kiureghian A., Ke J.-B. The stochastic finite element method in structural reliability // Probabilistic Eng. Mech. 1988. Vol. 3. № 2. P. 83–91.

Duncan J.M. Factors of safety and reliability in geotechnical engineering // J. Geotech. Geoenviron. 2000. Vol. 126. № 4. P. 307–316.

El-Ramly H., Morgenstern N.R., Cruden D.M. Probabilistic stability analysis of a tailings dyke on presheared clay-shale // Can. Geotech. J. 2003. Vol. 40. № 1. P. 192–208.

Farias M.M., Naylor D.J. Safety analysis using finite elements // Comput. Geotech. 1998. Vol. 22. № 2. P. 165–181.

Fenton G.A., Griffiths D.V. Bearing capacity prediction of spatially random c–ц soils // Can. Geotech. J. 2003. Vol. 40. № 1. P. 54–65.

GEO-SLOPE International Ltd. Stress-deformation modeling with SIGMA/W2007 version: an engineering methodology [computer program]. Calgary, Alberta, Canada: GEO-SLOPE International Ltd., 2010a.

GEO-SLOPE International Ltd. Stability modeling with SLOPE/W 2007 version: an engineering methodology [computer program]. Calgary, Alberta, Canada: GEO-SLOPE International Ltd., 2010b.

Ghanem R.G., Spanos P.D. Stochastic finite element: a spectral approach. Revised version. Mineola, New York: Dover Publication Inc., 2003.

Griffiths D.V., Fenton G.A. Probabilistic slope stability analysis by finite elements // J. Geotech. Geoenviron. 2004. Vol. 130. № 5. P. 507–518.

Griffiths D.V., Huang J.S., Fenton G.A. Probabilistic infinite slope analysis // Comput. Geotech. 2011. Vol. 38. № 4. P. 577–584.

Huang S.P. Simulation of random processes using Karhunen–Loeve expansion: Ph.D. thesis Singapore: National University of Singapore, 2001.

Isukapalli S.S., Roy A., Georgopoulos P.G. Stochastic response surface methods for uncertainty propagation: application to environmental and biological systems // Risk Anal. 1998. Vol. 18. № 3. P. 351–363.

Ji J., Liao H.J., Low B.K. Modeling 2-D spatial variation in slope reliability analysis using interpolated autocorrelations // Comput. Geotech. 2012. Vol. 40. P. 135–146.

Laloy E., Rogiers B., Vrugt J.A., Mallants D., Jacques D. Efficient posterior exploration of a high-dimensional groundwater model from two-stage MCMC simulation and polynomial chaos expansion // Water Resour. Res. 2013. Vol. 49. № 5. P. 2664–2682.

Li H., Zhang D. Probabilistic collocation method for flow in porous media: comparisons with other stochastic method // Water Resour. Res. 2007. Vol. 43. № W09409. P. 44–48.

Li D.Q., Chen Y.F., Lu W.B., Zhou C.B. Stochastic response surface method for reliability analysis of rock slopes involving correlated non-normal variables // Comput. Geotech. 2011. Vol. 38. № 1. P. 58–68.

Li D.Q., Jiang S.H., Chen Y.G., Zhou C.B. A comparative study of three collocation point methods for odd order stochastic response surface method // Struct. Eng. Mech. 2013a. Vol. 45. № 5. P. 595–611.

Li D.Q., Tang X.S., Phoon K.K., Chen Y.F., Zhou C.B. Bivariate simulation using copula and its application to probabilistic pile settlement analysis // Int. J. Numer. Anal. Methods Geomech. 2013b. Vol. 37. № 6. P. 597–617.

Li D.Q., Qi X.H., Phoon K.K., Zhang L.M., Zhou C.B. Effect of spatially variable shear strength parameters with linearly increasing mean trend on reliability of infinite slopes // Struct. Saf. 2013c. DOI: http://dx.doi.org/10.1016/j.strusafe.2013.08.005.

Liu W.K., Belytschko T., Mani A. Random field finite elements // Int. J. Numer. Methods Eng. 1986. Vol. 23. № 10. P. 1831–1845.

Low B.K., Lacasse S., Nadim F. Slope reliability analysis accounting for spatial variation // Georisk. 2007. Vol. 1. № 4. P. 177–189.

Lumb P. Safety factors and the probability distribution of soil strength // Can. Geotech. J. 1970. Vol. 7. № 3. P. 225–242.

Mollon G., Dias D., Soubra A.-H. Probabilistic analysis of pressurized tunnels against face stability using collocation-based stochastic response surface method // J. Geotech. Geoenviron. 2011. Vol. 137. № 4. P. 385–397.

Phoon K.K., Kulhawy F.H. Characterization of geotechnical variability // Can. Geotech. J. 1999. Vol. 36. № 4. P. 612–624.

Phoon K.K., Huang S.P., Quek S.T. Implementation of Karhunen-Loeve expansion for simulation using a wavelet-Galerkin scheme // Probabilistic Eng. Mech. 2002. Vol. 17. № 3. P. 293–303.

Srivastava A., Sivakumar Babu G.L. Effect of soil variability on the bearing capacity of clay and in slope stability problems // Eng. Geol. 2009. Vol. 108. № 1–2. P. 142–152.

Srivastava A., Sivakumar Babu G.L., Haldar S. Influence of spatial variability of permeability property on steady state seepage flow and slope stability analysis // Eng. Geol. 2010. Vol. 110. № 3–4. P. 93–101.

Stefanou G. The stochastic finite element method: past, present and future // Comput. Methods Appl. Mech. Eng. 2009. Vol. 198. № 9–12. P. 1031–1051.

Tabarroki M., Ahmad F., Banaki R., Jha S., Ching J. Determining the factors of safety of spatially variable slopes modeled by random fields // J. Geotech. Geoenviron. 2013. Vol. 139. № 12. P. 2082–2095.

Tang X.S., Li D.Q., Chen Y.F., Zhou C.B., Zhang L.M. Improved knowledge-based clustered partitioning approach and its application to slope reliability analysis // Comput. Geotech. 2012. Vol. 45. P. 34–43.

Tang X.S., Li D.Q., Rong G., Phoon K.K., Zhou C.B. Impact of copula selection on geotechnical reliability under incomplete probability information // Comput. Geotech. 2013. Vol. 49. P. 264–278.

Vanmarcke E.H. Probabilistic modeling of soil profiles // J. Geotech. Eng. Div. 1977. Vol. 103. № 11. P. 1227–1246.

Vanmarcke E.H. Random fields: analysis and synthesis. Revised and expanded new edition. World Beijing: Scientific Publishing, 2010.

Vorechovsky M. Simulation of simply cross-correlated random fields by series expansion methods // Struct. Saf. 2008. Vol. 30. № 4. P. 337–363.

Wang Y., Cao Z.J., Au S.K. Practical reliability analysis of slope stability by advanced Monte Carlo simulations in a spreadsheet // Can. Geotech. J. 2011. Vol. 48. № 1. P. 162–172.

Wolff T.F. Analysis and design of embankment dam slopes: a probabilistic approach: Ph.D. thesis. Lafayette, Ind, USA: Purdue University, 1985.

Zhang J., Huang H.W., Juang C.H., Li D.Q. Extension of Hassan and Wolff method for system reliability analysis of soil slopes // Eng. Geol. 2013. Vol. 160. P. 81–88.

Zhu H., Zhang L.M. Characterizing geotechnical anisotropic spatial variations using random field theory // Can. Geotech. J. 2013. Vol. 50. № 7. P. 723–734.