Магия трансформации координат: от местного к глобальному
 Гладышев Александр КонстантиновичЗаместитель начальника отдела строительного проектирования департамента капитального строительства АО «Концерн ВКО «Алмаз-Антей»
Гладышев Александр КонстантиновичЗаместитель начальника отдела строительного проектирования департамента капитального строительства АО «Концерн ВКО «Алмаз-Антей» Никифоров Николай ВасильевичГенеральный директор и основатель компании Soilbox, резидента «Сколково» и Московского инновационного кластера
Никифоров Николай ВасильевичГенеральный директор и основатель компании Soilbox, резидента «Сколково» и Московского инновационного кластераЧасто изыскатели, не имеющие специального геодезического образования, испытывают трудности при переводе координат из одних систем в другие. Также возникает много вопросов по системам координат в целом и границам их применимости. В связи с этим в статье рассматриваются основные современные земные геодезические координатные системы, границы их применимости и назначение. Приводится подробный алгоритм пересчета из системы координат WGS-84 в местные системы координат Российской Федерации. На основании расчетов создан открытый интерактивный веб-сервис wgs-msk.soilbox.app, приводится оценка точности пересчета.
Координация пространства: от древних звезд к современной геодезии
Земные геодезические системы координат
Почему мы используем разные системы координат
Наиболее распространенные системы координат в России и СНГ
Пересчет координат из WGS-84 в МСК
Делаем интерактивный веб-сервис
ВВЕДЕНИЕ
Оглядываясь на наш опыт решения задач в изысканиях, строительстве и кадастре, мы часто сталкивались с тем, что специалисты, не имеющие специального геодезического образования, испытывают сложности при работе с системами координат.
Наибольшую сложность обычно вызывает трансформация координат между популярными в России системами МСК (местная система координат) и WGS-84 (World Geodetic System 1984), которая, например, является стандартом устройств Garmin и прочих навигационных приемников. И это неслучайно. Ведь в открытых источниках не так много информации на русском языке, предоставляющей сведения по данному вопросу в структурированном и простом виде. А рыться в учебниках по геодезии самостоятельно осмелится далеко не каждый. Поэтому перед нами встала задача создать простое алгоритмическое решение по трансформации координат, которое было бы интерактивно, функционально, основывалось на современных технологиях и работало как веб-сервис.
Мы подумали, почему бы не сделать такое решение общедоступным с детальным разбором механизма пересчета. Хотим поделиться с вами результатами нашей работы. Для этого начнем наше путешествие с погружения в историю координации пространства на разных этапах становления человеческих цивилизаций.
КООРДИНАЦИЯ ПРОСТРАНСТВА: ОТ ДРЕВНИХ ЗВЕЗД К СОВРЕМЕННОЙ ГЕОДЕЗИИ
С древнейших времен люди стремились понять и измерить мир вокруг себя. В эпоху древних цивилизаций, таких как Египет и Вавилон, использовались простые системы координат (способы определения положения и перемещения на местности с помощью чисел или других символов в плоской прямоугольной системе), основанные на земных опорных точках (системах межевых линий, дорогах, городах, системах водоснабжения и проч.) и звездных ориентирах. Эти системы позволяли строить пирамиды и архитектурные сооружения с удивительной точностью (рис. 1).

В древней Греции ученые впервые начали использовать более сложные системы координат. Эратосфен (276 год до н. э. – 194 год до н. э.), например, смог вычислить окружность Земли, используя простую систему координат, основанную на измерении теней.
Средневековые картографы и астрономы развивали эти идеи, создавая более сложные системы координат. Они использовали эти системы для создания более точных карт и в морской навигации.
В эпоху Возрождения с развитием математики и астрономии системы координат стали еще более сложными и точными. Это привело к созданию первых геодезических систем координат, которые использовались для измерения Земли на больших расстояниях. Начало эпохи Возрождения (примерно XVI век) ознаменовалось крайне важным переходом от геоцентрической модели мира (начало отсчета системы координат – в центре масс Земли) к гелиоцентрической (начало отсчета системы координат – в центре масс Солнца), что в разы повысило точность астрономических измерений.
В XIX–XX веках с развитием технологий и науки появились новые методы измерений и новые системы координат. Это привело к созданию современных геодезических систем координат, таких как WGS-84, которые используются сегодня в любых отраслях – от спутниковой навигации до моделирования климата [1].
Сегодня мы используем самые разные системы координат, которые позволяют измерять и постигать мир вокруг нас с невероятной точностью. Они являются результатом тысячелетнего развития и инноваций и продолжают совершенствоваться по мере того, как мы продолжаем исследовать и понимать наш мир.
ЗЕМНЫЕ ГЕОДЕЗИЧЕСКИЕ СИСТЕМЫ КООРДИНАТ
Системы координат, применяемые в геодезии и смежных с ней дисциплинах, можно классифицировать по различным признакам. Например по области их приложения: астрономические, геодезические, спутниковые, картографические, фотограмметрические и др.; по уровню глобализации: мировые, общеземные, национальные и т. д. Однако наиболее часто применимы классификации, основанные на выборе:
- начала отсчета системы координат (планетоцентрические, квазипланетоцентрические и топоцентрические);
- направления осей координат (звездные, квазарные и земные);
- основной координатной плоскости (экваториальные, эклиптические, орбитальные и горизонтальные).
Мы рассмотрим только земные системы координат. Чтобы разобраться в этом вопросе, в первую очередь определим, что относится к земным геодезическим системам координат.
К земным геодезическим системам координат относятся такие системы координат, которые жестко связаны с Землей, то есть системы, вращающиеся вместе с Землей и участвующие в ее суточном вращении.
Положение точек непосредственно на физической поверхности Земли или в околоземном пространстве, а также на поверхности земного эллипсоида (математической модели Земли) может определяться в различных как прямолинейных (прямоугольных), так и криволинейных (ортогональных) системах координат.
Давайте рассмотрим три наиболее часто используемые системы координат:
- пространственные прямоугольные декартовы системы координат X, Y, Z;
- криволинейные эллипсоидальные геодезические координаты B, L, H;
- плоские прямоугольные декартовы системы координат х, y.
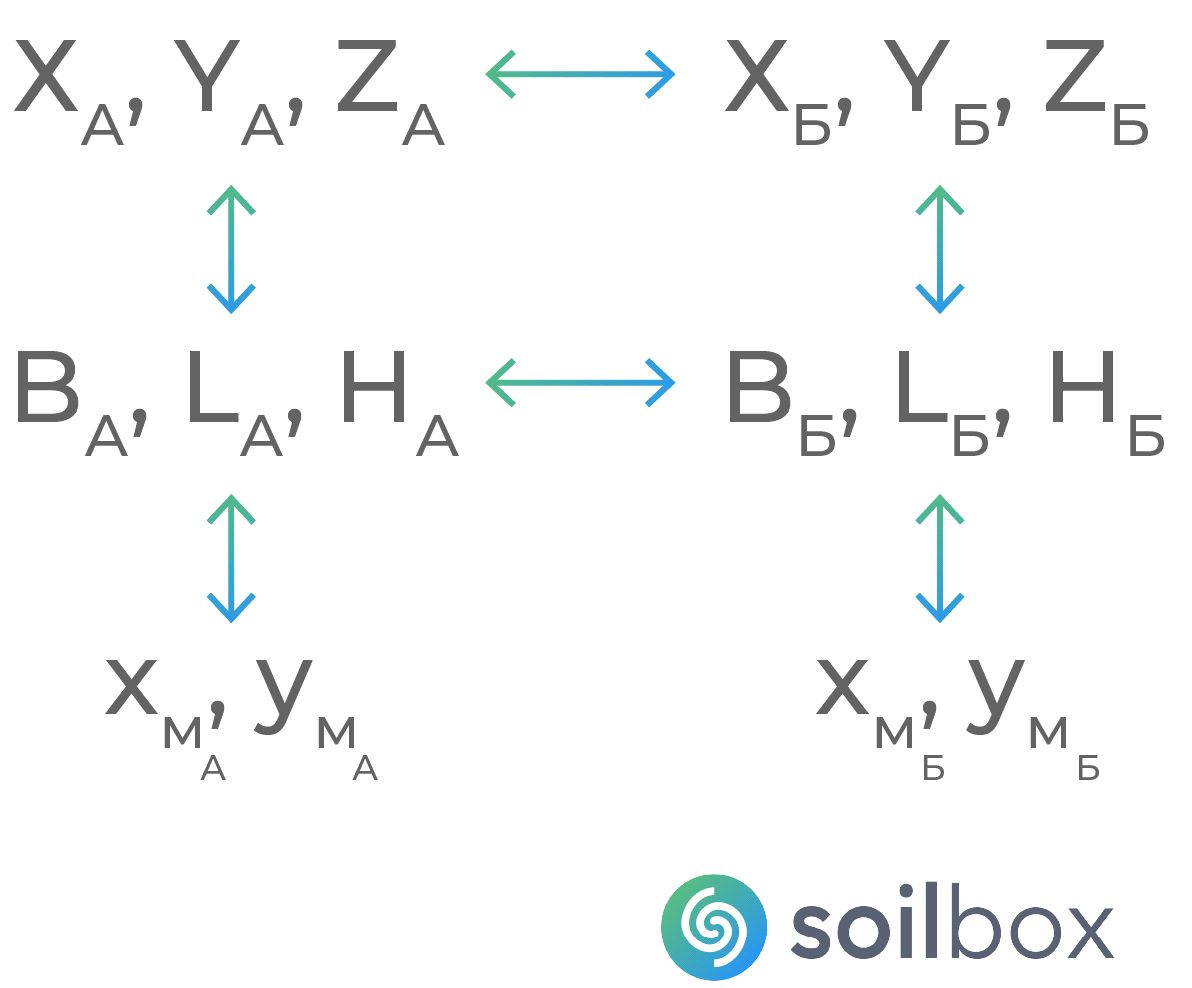
В пространственных прямоугольных системах координат началом является центр эллипсоида вращения, а направления осей связываются с положением полюса Земли, ее экватора и меридиана Гринвича. Ось аппликат (Z) направлена на север по оси вращения Земли, ось абсцисс (Х) совпадает с линией пересечения земного экватора и плоскостью Гринвичского меридиана, а ось ординат (Y) дополняет систему до правой. Пространственные прямоугольные системы координат позволяют определять координаты точек не только на эллипсоиде, но и вне его, то есть на земной поверхности и вне ее.
Положение любой точки пространства будет однозначно определяться тремя координатами (рис. 2): абсцисса равна отрезку ОР1 (Х = ОР1), ордината соответствует отрезку координатной оси ОР2 (Y = ОР2), а аппликата равна отрезку ОР3 (Z = ОР3). Данная система широко используется в спутниковых определениях положения точек, так как для ее применения не нужно иметь поверхность относимости (поверхность эллипсоида вращения), из-за чего отсутствует необходимость в редуцировании результатов полевых измерений на поверхность относимости (эллипсоид, сферу).
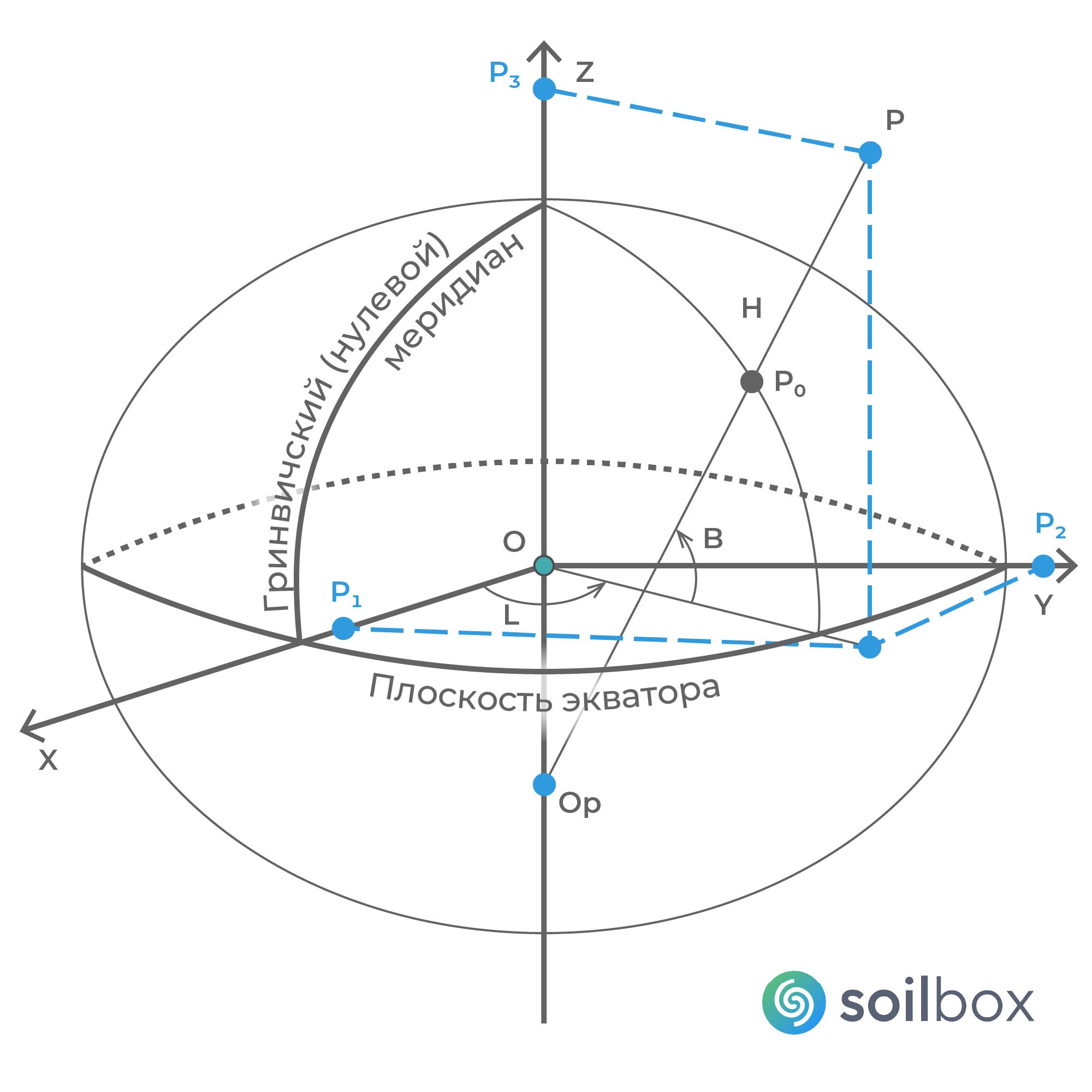
Криволинейные эллипсоидальные (геодезические координаты) системы геодезических координат связаны с математической моделью земной поверхности – эллипсоидом вращения, форма и размеры которого с определенной степенью точности соответствуют форме и размеру Земли.
Положение точки на земной поверхности или в околоземном пространстве будет определяться тремя величинами, две из которых угловые (широта В, долгота L) и одна линейная (высота Н). В – это угол, составленный плоскостью экватора и нормалью POP к поверхности эллипсоида в данной точке P. L – это двухгранный угол, составленный плоскостью начального геодезического меридиана, проходящего через обсерваторию в Гринвиче, и плоскостью геодезического меридиана, проходящего через заданную точку P. H – отрезок нормали PоP от поверхности эллипсоида до данной точки P (см. рис. 2).
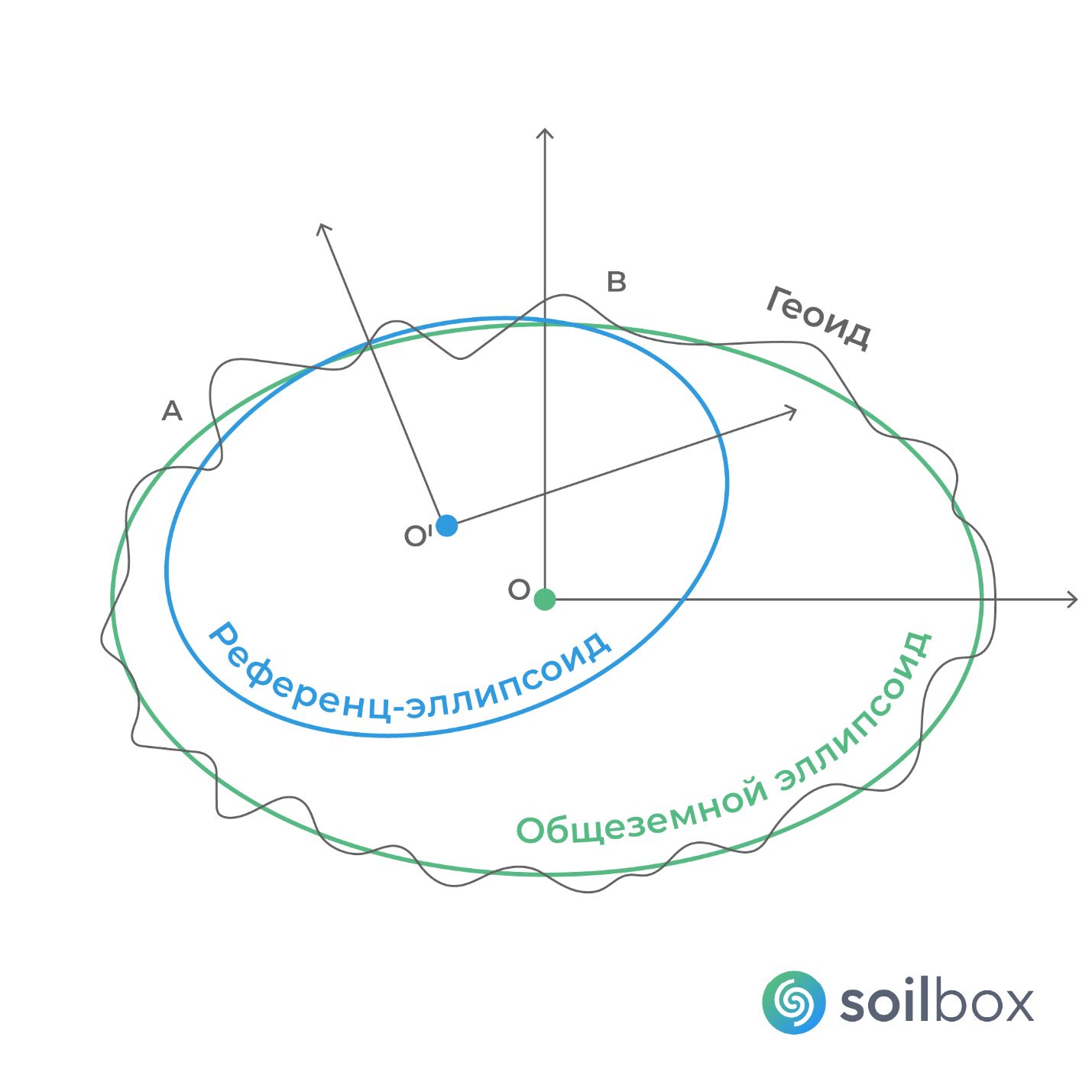
Если центр эллипсоида вращения совпадает с центром масс Земли, плоскость экватора эллипсоида совпадает с плоскостью земного экватора, а суммы квадратов уклонений по высоте геоида 1 от поверхности эллипсоида во всех его точках минимальны, то такая система является геоцентрической, а эллипсоид называется общим земным эллипсоидом (ГСК-2011, ПЗ-90.11, ITRS, WGS-84 [2]). (Напомним, что геоид – это близкое к реальности представление физической формы Земли без учета особенностей рельефа, представляющее собой выпуклую замкнутую поверхность. Эта поверхность приблизительно соответствует среднему уровню вод Мирового океана в состоянии покоя, а также условно продолжается под континентами. При этом в каждой его точке направление силы тяжести перпендикулярно его поверхности.)
Если используется эллипсоид, параметры которого были рассчитаны по результатам измерений, охватывающих территорию одного или нескольких прилегающих государств, такие эллипсоиды принято называть референц-эллипсоидами (например, референц-эллипсоид Красовского), а системы координат – региональными (государственные – СК42) (рис. 3).
В геоцентрических и региональных системах координат координаты для точки на поверхности Земли или в околоземном пространстве могут записываться как в виде пространственных прямоугольных координат (например: X=3166151,882 м; Y=2016439,241 м; Z=5139515,764 м), так и в виде криволинейных эллипсоидальных координат (например: B=54°02'23,68925'' N; L=032°29'31,17590'' E; H=200,0 м).
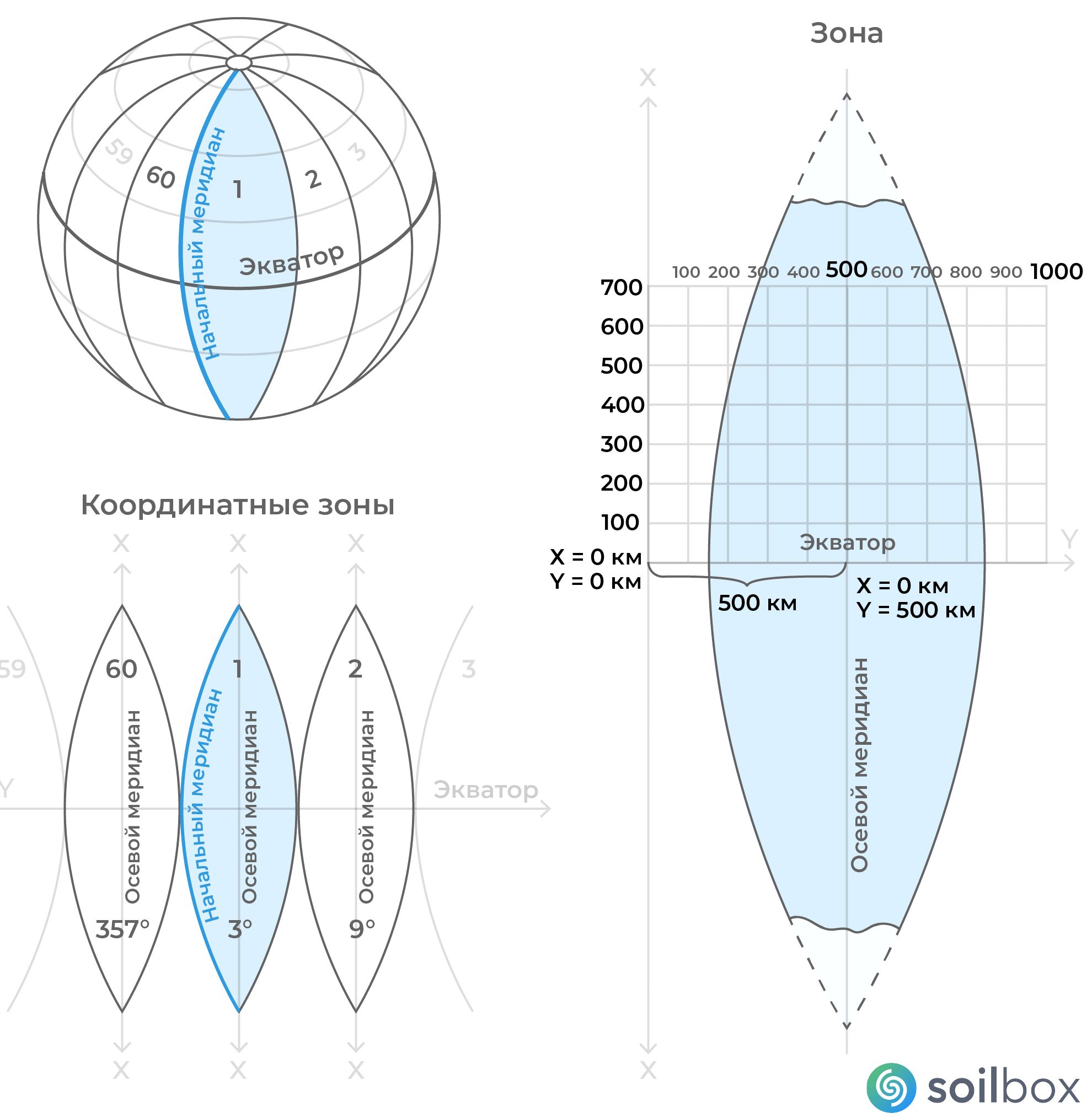
Плоские прямоугольные координаты получают путем отображения поверхности эллипсоида как математической модели Земли на плоскость по тому или иному математическому закону (в той или иной картографической проекции). Изображение осевого меридиана (меридиана, проходящего посередине зоны проекции) и экватора эллипсоида на плоскости принимаются за координатные оси, а точка их пересечения – за начало системы действительных плоских систем прямоугольных координат. При этом ось абсцисс (x) направлена на север, а ось ординат (y) – на восток. В государственных системах координат России (СССР) для всех точек на территории нашей страны абсциссы имеют положительное значение. Для того чтобы ординаты точек также были положительными, в каждой зоне ординату начала координат принимают равной 500 км (рис. 4) [3].
ПОЧЕМУ МЫ ИСПОЛЬЗУЕМ РАЗНЫЕ СИСТЕМЫ КООРДИНАТ
Геоцентрические координаты, будучи общими, глобальными (едиными) для всей Земли в целом, применяются для решения задач, связанных с изучением всей Земли как планеты, то есть для решения геодезических задач между точками, удаленными друг от друга на большие расстояния.
Однако при производстве массовых наземных работ, предназначенных для решения локальных практических задач (производства топографических съемок, создания геодезического обеспечения для строительства и эксплуатации крупных инженерно-технических сооружений, сопровождения инженерных изысканий и других, выполняемых, как правило, на сравнительно небольших территориях), применение общеземных и референцных систем координат становится неудобным и даже обременительным.
Поэтому в практике ведения инженерных геодезических работ обычно используются системы плоских прямоугольных координат. Их основными преимуществами являются простота и удобство, а также возможность при обработке геодезических измерений использовать формулы плоской геометрии и тригонометрии, позволяющие существенно упростить вычисления.
Но земная поверхность, как и ее математическая модель – эллипсоид вращения, не является плоскостью. Поэтому не может быть предложена система плоских прямоугольных координат, в которой без искажений могло бы быть выражено взаимное положение точек земной поверхности. Исследования кривизны земного эллипсоида показывают, что только весьма небольшие участки его поверхности можно принимать за плоскости. Так, например, при искажениях, не превышающих 1 мм, можно принимать за плоскость участок земной поверхности радиусом не более 5–6 км [1].
В сравнительной таблице 1 приведены значения длины дуги в 33 секунды на плоскости: на осевом меридиане и удалении на 1,5 и 3 градуса от него, а также на разных широтах (рис. 5).
Таблица 1. Длина дуги на эллипсоиде и на плоскости (в проекции Гаусса – Крюгера)
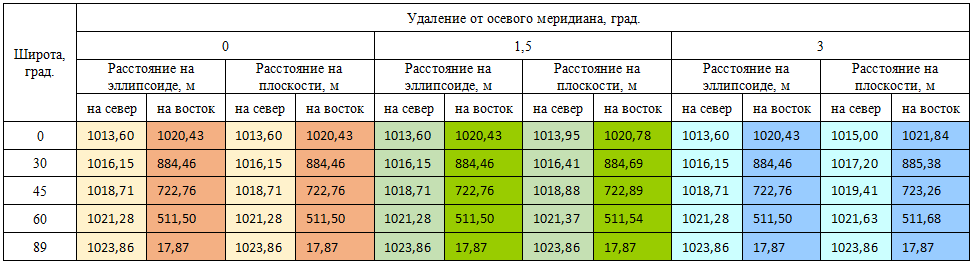
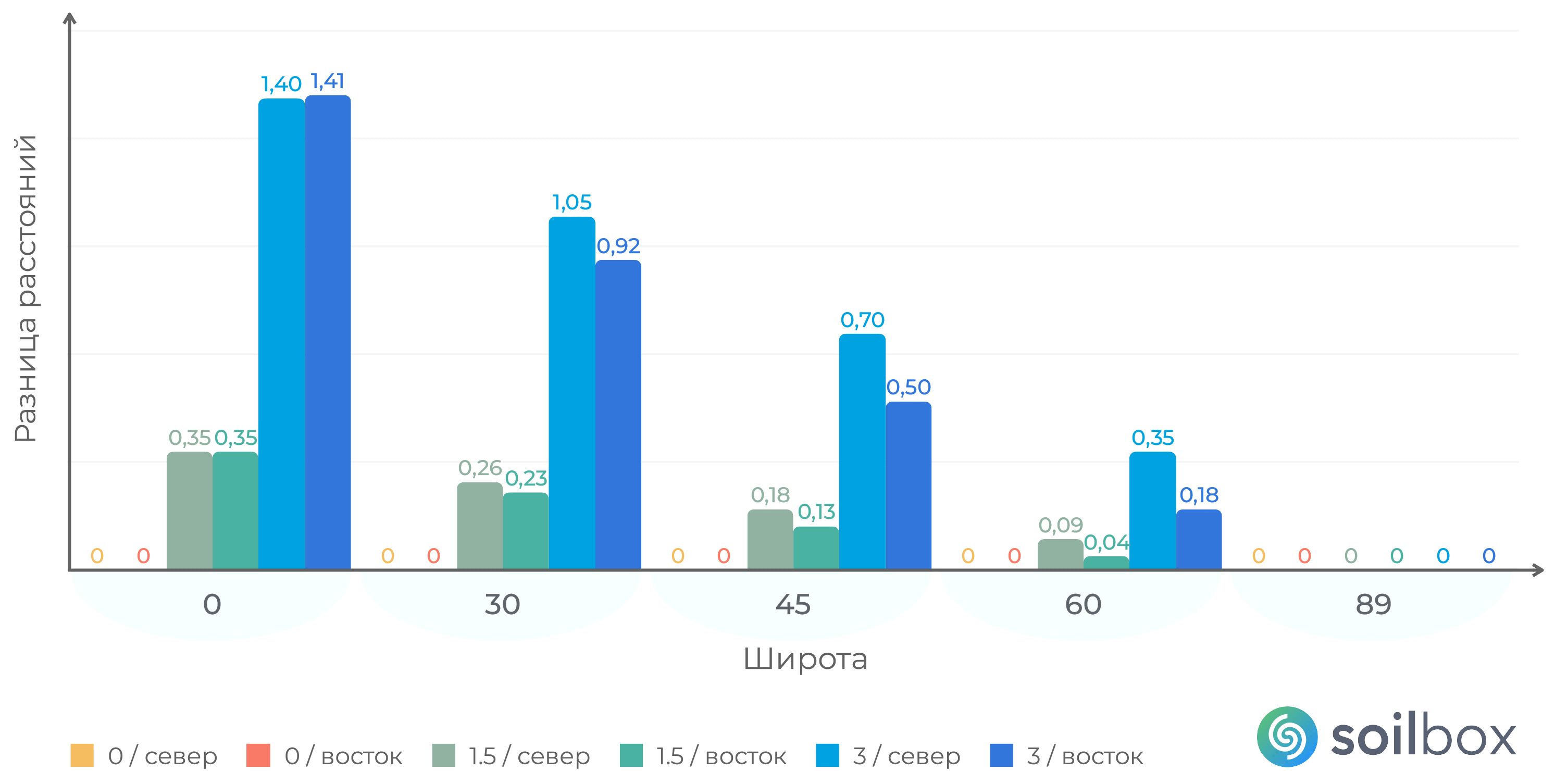
Как видно из таблицы 1 и диаграммы (см. рис. 5), расстояние в линейной мере одной и той же длины дуги разное в зависимости от широты, но на эллипсоиде оно не зависит от удаления точки от осевого меридиана в отличие от проекции. При этом видно, что разность расстояний, полученных на эллипсоиде и на плоскости, изменяется в зависимости от удаления от экватора и осевого меридиана.
Расстояния, рассчитанные по координатам на плоскости и фактически измеренные на земле, могут различаться. Особенно это актуально для линейных объектов, располагающихся параллельно экватору (с запада на восток), и участков, находящихся на краях зон проекции. Для исключения данных ошибок необходимо вводить масштабный коэффициент для каждого участка при проведении наземных измерений электронными тахеометрами, а для работы в графических программах вводить соответствующие системы координат.
Чтобы структурировать представление о параметрах наиболее часто используемых координатных систем, в таблице 2 сопоставлены основные характеристики трех земных систем отсчета: на общеземном эллипсоиде (геоцентрические системы координат), на референц-эллипсоиде (региональные системы координат) и на плоскости (местные системы координат).
Таблица 2. Характеристики координатных систем
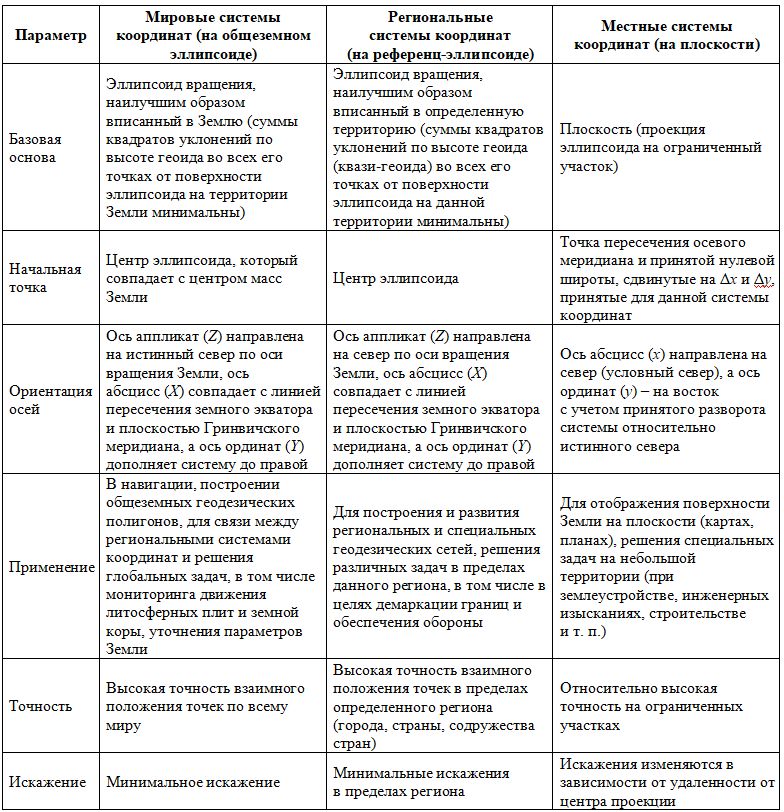
Проанализировав приведенную выше информацию, давайте сформулируем основные причины использования различных систем координат.
Специфика применения. Решение конкретной задачи опирается на определенную систему координат. Например, для решения задач на ограниченной территории в области кадастра, строительства и мониторинга, а также составления картографической продукции на бумажных носителях (картах и планах) принято использовать плоские прямоугольные координаты. Однако для решения задач, связанных с позиционированием с помощью глобальной навигации (например, GPS, ГЛОНАСС), мониторингом движения литосферных плит, картографическими работами на больших территориях (стран и сопредельных государств, Земли), используются пространственные прямоугольные или эллипсоидные системы координат.
Точность. Разные системы координат могут обеспечивать разную точность в зависимости от отображаемой площади и территории. Например, пространственные прямоугольные или эллипсоидные системы координат на базе общеземного эллипсоида обеспечивают высокую точность взаимного положения точек практически по всему миру, однако в некоторых регионах могут использоваться референц-эллипсоиды, которые обеспечивают еще большую точность на ограниченной территории. Применение плоских прямоугольных систем координат на ограниченных участках земной поверхности позволяет получать высокую (субмиллиметровую) [4] точность взаимного положения точек при выполнении работ с использованием оптико-электронных и лазерных средств измерений.
Исторические причины. Многие системы координат были разработаны десятилетия или даже столетия назад и продолжают использоваться традиционно. Например, многие страны и города имеют свои собственные системы координат, которые были разработаны до появления общеземных систем координат, таких как WGS-84, ITRS, ПЗ-90. В настоящий период идет постепенный переход к общеземным системам координат, но, учитывая огромный объем данных, в том числе в аналоговом виде, и вопросы, связанные с секретностью, процесс этот будет долгим.
Легальные и регулятивные требования. В большинстве случаев выбор системы координат определен законодательством, регулятивными требованиями или общепринятыми нормами [5, 6]. Например, в некоторых странах законодательство требует использовать определенную систему координат для выполнения отдельных видов геодезических или картографических работ, а для проведения международных исследований в настоящее время принята система ITRS (ITRF 2020).
НАИБОЛЕЕ РАСПРОСТРАНЕННЫЕ СИСТЕМЫ КООРДИНАТ В РОССИИ И СНГ
На сегодняшний день в России и странах СНГ используются самые разные системы координат в зависимости от конкретных задач и областей применения. Назовем наиболее распространенные из них.
Система отсчета ITRF2020 (International Terrestrial Reference Frame) – это реализация международной земной системы координат (ITRS), которая представляет собой пространственную прямоугольную декартову систему координат и используется для точных геодезических и геодинамических измерений на международном и межгосударственном уровнях.
Система координат WGS-84 – это общеземная система координат, которую использует американская система глобального навигационного спутникового позиционирования GPS. Она представляет собой трехмерную систему координат, основанную на общеземном эллипсоиде вращения.
Система координат ПЗ-90.11 («Параметры Земли 1990 года») – это общеземная система координат, которую использует российская система глобального навигационного спутникового позиционирования GLONASS. Она представляет собой трехмерную систему координат, основанную на общеземном эллипсоиде вращения.
Система координат СК-42 («Система координат 1942 года») – это региональная (референцная) система координат, которая использовалась в СССР для геодезических и картографических целей. Она реализована на референц-эллипсоиде Красовского. В ней координаты для точки на поверхности Земли могут быть записаны как в виде пространственных прямоугольных координат (X, Y, Z) и криволинейных эллипсоидальных координат (B, L, H), так и в виде плоских прямоугольных координат (x, y), которые являются поперечно-цилиндрической проекцией Гаусса – Крюгера эллипсоида Красовского с шириной зоны 6°. Для исключения отрицательных координат по оси ординат (у) и возможности однозначно определять номер зоны начало отсчета сдвигают на 500 км на восток и добавляют номер зоны n:
y = y' + n500000,
где y' – значение ординаты, полученное из вычислений.
Системы координат МСК – это плоские прямоугольные системы координат, которые используются для местных и региональных нужд (выполнения инженерных изысканий, ведения кадастра, сопровождения строительства). В России и странах СНГ существует множество различных МСК, каждая из которых применяется для определенного региона.
ПЕРЕСЧЕТ КООРДИНАТ ИЗ WGS-84 в МСК
Системы координат WGS-84, ГСК-2011 и ПЗ-90.11 являются геоцентрическими (центр масс Земли совпадает с центром эллипсоидов вращения), а эллипсоиды вращения – общеземными. Системы координат СК-95 и СК-42 являются региональными (центр масс Земли не совпадает с центром эллипсоида вращения) и реализуются на референц-эллипсоиде Красовского.
Местные системы координат являются плоскими прямоугольными и на территории России реализуются преимущественно с помощью проекции Гаусса – Крюгера (равноугольной, конформной) референц-эллипсоида Красовского на плоскость с шириной зон 6, 3 и 1,5 градуса.
В общем случае границы местных систем координат соответствуют географическим границам федеральных субъектов РФ. Например, границы МСК-01 будут соответствовать географическим границам федерального субъекта Республики Адыгея. Номер федерального субъекта и номер МСК также чаще всего совпадают: 01 – Республика Адыгея, 02 – Республика Башкортостан и так далее (рис. 6).
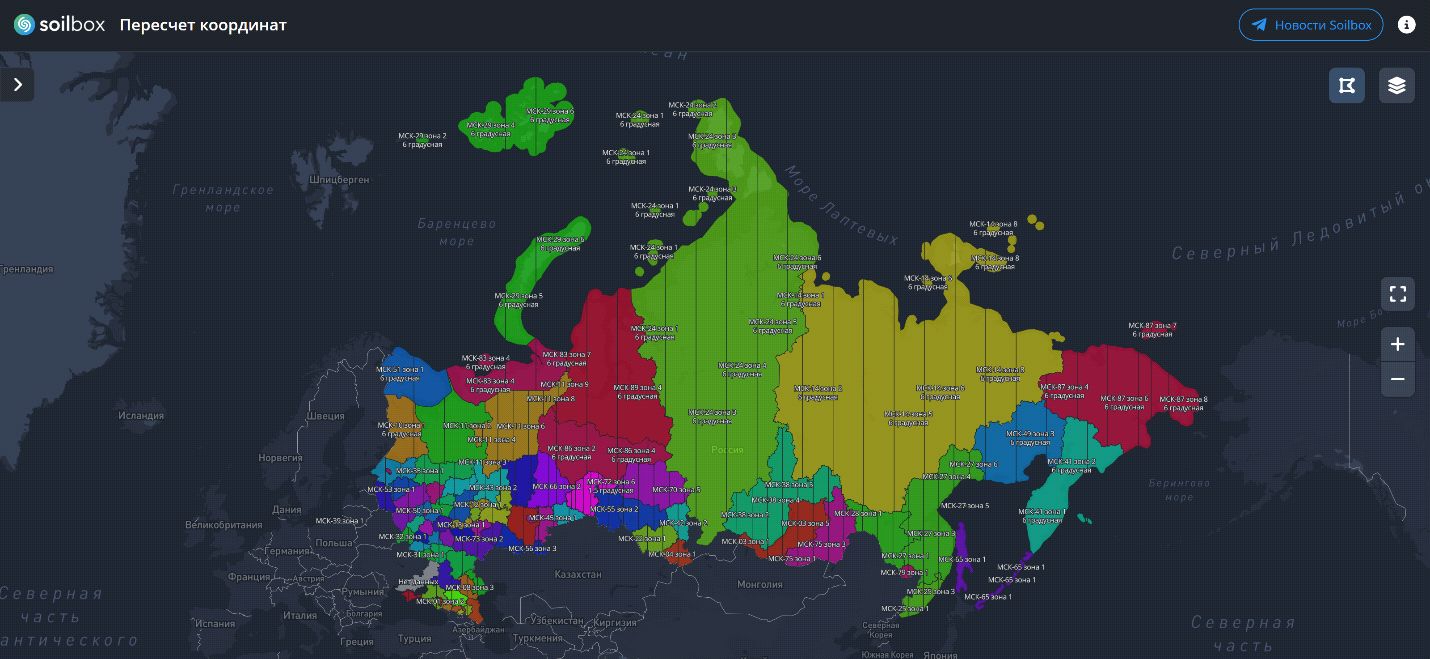
Однако осевые меридианы зон чаще всего не соответствуют географическому положению той или иной МСК, так как они были унаследованы в большинстве случаев от СК-63. Например, осевые меридианы для зоны 1 и зоны 2 МСК-01 (Республика Адыгея) находятся по краям федерального округа (ширина республики – 2 градуса). Таким образом, каждая МСК делится дополнительно на зоны шириной 6, 3 или 1,5 градуса вдоль меридиана. Каждая зона имеет свой осевой меридиан, тем самым разделяя МСК на участки произвольного размера параллельно меридиану. То есть для зоны 1 МСК-01 географические границы будут представлены в виде результата пересечения двух полигонов: полигона с географическими границами МСК-01 (Республика Адыгея) и полосы с границами (рис. 7):
[осевой меридиан зоны – ширина зоны/2;
осевой меридиан зоны + ширина зоны/2].
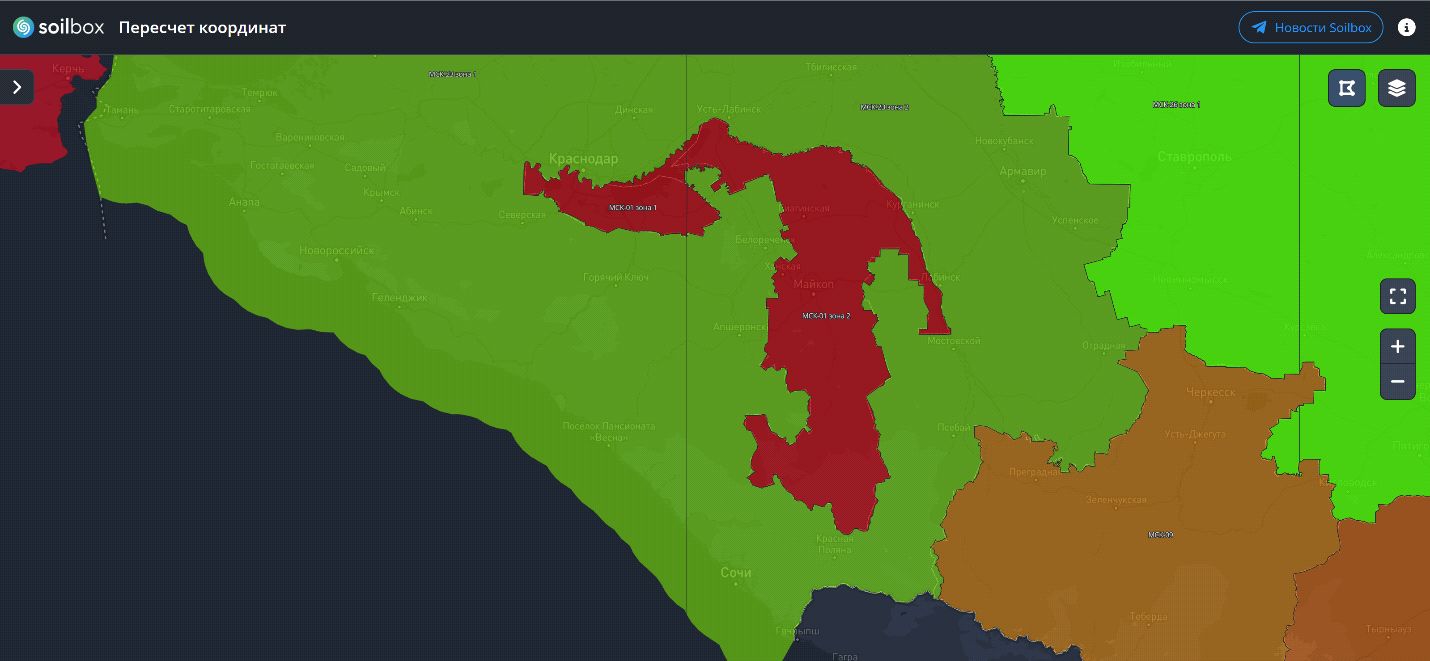
Учитывая, что в настоящее время широко применяется спутниковая аппаратура, которая работает в системе координат WGS-84, а инженерные изыскания, проектирование и кадастровые работы ведутся преимущественно в местных системах координат, возникает необходимость во взаимном преобразовании координат.
Для выполнения взаимных преобразований из одной системы в другую с необходимой точностью в геодезической литературе имеются формулы, которые позволяют решать эти задачи с высокой точностью (рис. 8).
Рассмотрим пример наиболее часто встречающейся задачи, с которой сталкиваются специалисты в Российской Федерации, – пересчета координат, полученных с помощью навигационных приемников типа GARMIN, из геоцентрической системы координат WGS-84 в местную систему координат, принятую для ведения кадастра. Данную процедуру можно выполнить в два этапа.
1. Переход из системы координат WGS-84 (BWGS-84, LWGS-84, HWGS-84) в систему координат СК-42/СК-95, реализованную на референц-эллипсоиде Красовского (BСК-42, LСК-42, HСК-42).
2. Переход от референц-эллипсоида Красовского к плоским прямоугольным координатам путем проекции Гаусса – Крюгера.
Первый этап пересчета
Для выполнения первого этапа нам понадобятся следующие исходные данные.
1. Геодезические координаты точки в системе координат А (WGS-84), полученные с помощью навигационного приемника (B – геодезическая широта, L – геодезическая долгота, H – геодезическая высота). Для примера возьмем точку, расположенную в Астраханской области, которая попадает в местную систему координат МСК-30 зона 2:
- BА = 46°17'47,07144'';
- LА = 48°00'57,18644'';
- HА = -20 м
2. Параметры общеземного эллипсоида WGS-84 (системы координат А) и референц-эллипсоида Красовского (системы координат Б) (таблица 3) [7, 8]:
Таблица 3. Параметры общеземного эллипсоида WGS-84 и референц-эллипсоида Красовского

3. Семь параметров трансформации для перехода из системы координат WGS-84 в систему координат СК-42 таблица 4) [2, 9]:
Таблица 4. Параметры трансформации для перехода из системы координат WGS-84 в систему координат СК-42

Для обратного перехода из СК-42 в WGS-84 данные параметры берутся с противоположным знаком.
В общем виде преобразование геодезических координат из системы А (WGS-84) в систему Б (СК-42) можно записать так:
- BБ=BA+ΔB;
- LБ=LA+ΔL;
- HБ=HA+ΔH,
где ΔB, ΔL, ΔH – поправки к геодезическим координатам точки.
Для расчета поправок нам потребуется вычислить следующие дополнительные элементы.
1. Разность больших полуосей эллипсоидов:
Δа = аБ – аА;
2. Квадраты первых эксцентриситетов эллипсоидов:
е2А = 2×αА – α2А; е2Б = 2×αБ – α2Б;
3. Разность квадратов первых эксцентриситетов эллипсоидов:
Δе2 = е2Б – е2А;
4. Среднее значение большой полуоси двух эллипсоидов:
a = (aA + aБ) / 2;
5. Среднее значение квадратов первых эксцентриситетов эллипсоидов:
e2 = (е2А + е2Б) / 2;
6. Радиус кривизны первого вертикала:

7. Радиус кривизны меридианного сечения:

После получения значений данных элементов и принимая число угловых секунд в 1 радиане
ρ = (180/π)×3600 = 206264,806,
рассчитаем поправки к геодезическим координатам по формулам:
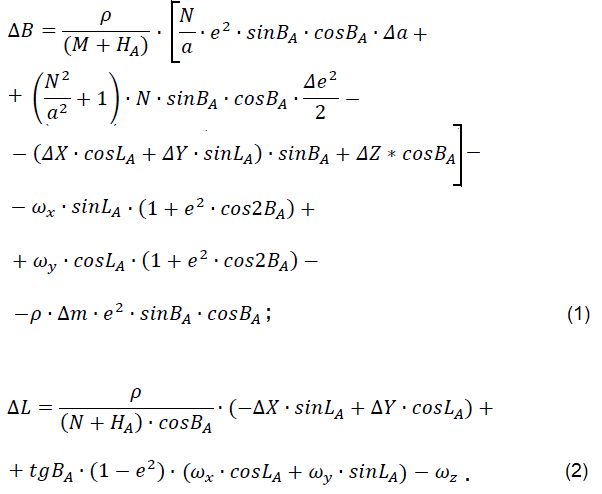
Подставляя известные значения в формулы (1) и (2), получим:
ΔB = -0,152''; ΔL = +4,704''.
Соответственно:
BБ = 46°17'46,91930''; LБ = 48°01'01,89076''.
В приведенном примере расчет поправок выполнен с погрешностью, не превышающей 0,3 м (в линейной мере), что превышает точность навигационных координат. Для достижения погрешности не более 0,001 м необходимо выполнить вторую итерацию, то есть учесть значения поправок к геодезическим координатам и повторно выполнить вычисление поправок ΔB и ΔL. При этом формулы для определения широты и долготы будут иметь вид:

Второй этап пересчета
Для выполнения второго этапа нам понадобятся параметры эллипсоида Красовского из первого этапа и следующие данные.
1. Параметры эллипсоида Красовского:
- размер большой полуоси aБ = 6378245 м;
- сжатие эллипсоида aБ = 1:298,3;
- квадрат первого эксцентриситета е2 = 6,69342162297×10-3.
2. Рассчитанные выше значения геодезических координат:
- BБ = 46°17'46,91930'';
- LБ = 48°01'01,89076''.
3. Параметры проекции, полученные из открытых источников (для МСК-30 зона 2):
- осевой меридиан L0 = 49,05°;
- масштабный коэффициент, равный 1;
- начальная широта, равная 0°;
- линейные смещения Δx = -4714743,504 м; Δy = 2300000 м [10]:
Для использования формулы трансформации нам потребуется вычислить следующие дополнительные элементы.
1. Разность долгот:
l = LБ – L0 = -1°01'58,10924''.
2. Радиус кривизны первого вертикала:
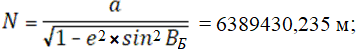
3. Проекция полного уклонения отвесных линий на плоскость первого вертикала:
η2 = e2 × cos2BБ / (1 – e2) = 0,0032168497817.
4. Коэффициенты G0, G1, G2, G3:
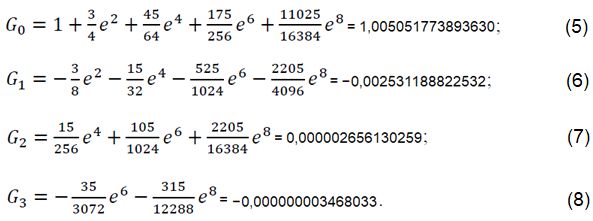
Данные коэффициенты являются постоянными для эллипсоида.
5. Длина дуги меридиана от экватора до параллели с широтой В:
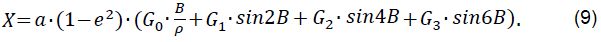
Данная формула позволяет получить значение длины дуги с погрешностью, не превышающей 0,2 мм.
После получения значений данных элементов можем рассчитать действительные плоские прямоугольные координаты:
x = X + ΔX = 5129637,23 м,
где длина дуги Х = 5129118,703 м,
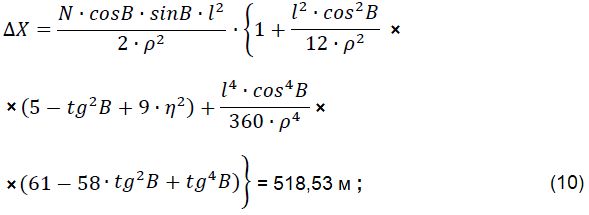
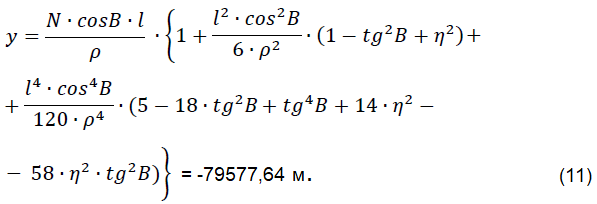
Переход от действительных плоских прямоугольных координат к местным плоским прямоугольным координатам осуществляется по следующим формулам:
х' = х + Δx = 414893,73 м;
y' = y + Δy = 2220422,36 м.
В итоге получили координаты точки в МСК-30 зона 2 с линейной точностью 0,3 м без учета ошибок исходных данных (точность определения абсолютных координат точки в WGS-84).
При необходимости возможен и обратный пересчет из местных плоских прямоугольных координат в геодезические в системе координат WGS-84.
В настоящее время практически все современные ГИС и программы для оформления картографической продукции (создания карт и топопланов), а также для обработки геодезических измерений позволяют задать пользовательскую систему координат или выбрать из заложенных в ГИС или программах.
Пересчет в данных программах между эллипсоидами обычно выполняется через пространственные прямоугольные координаты (X, Y, Z) и параметры трансформации, в большинстве случаев расчетные, а не принятые по нормативным документам. В случае выполнения пересчетов с использованием разных программных продуктов по установленным в них параметрам перехода это может привести к расхождению результатов вычислений величиной до десятков метров. Для исключения таких расхождений рекомендуется проверять установленные параметры пересчета и в случае их несоответствия нормативным документам выполнять корректировку или калибровку параметров по точкам с известными координатами в заданных системах [2].
Учитывая наличие огромного количества различных эллипсоидов, систем координат и проекций, необходимо очень внимательно подходить к данному выбору, так как неправильно выбранный эллипсоид или проекция могут дать ошибку в плоских прямоугольных координатах в десятки и сотни метров.
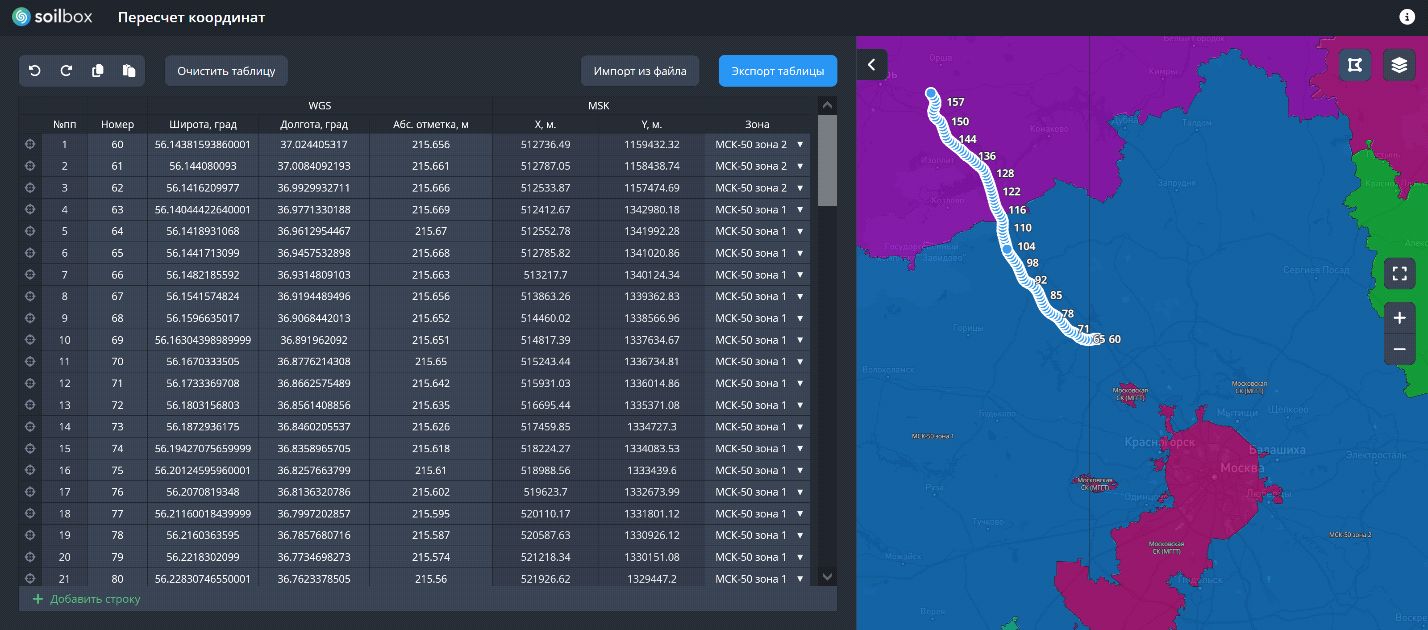
ДЕЛАЕМ ИНТЕРАКТИВНЫЙ ВЕБ-СЕРВИС
Тем не менее, несмотря на большое изобилие решений по трансформации координат, за все время работ нам не удалось встретить такого, которое было бы достаточно современно, интерактивно и решало бы за пользователя рутинные задачи. При общении с нашими коллегами и клиентами мы собрали основные требования, которым должен отвечать современный веб-сервис пересчета координат.
1. Интерактивность -- способность сервиса оперативно реагировать на действия пользователя
2. Автоматическое назначение зон МСК. Сейчас во всех программах при пересчете координат из WGS в МСК нужно задавать вручную зоны МСК для пересчитываемых точек, хотя они могут быть определены автоматически в соответствии с их географическими координатами WGS. Особенно это актуально на протяженных линейных объектах, пересекающих несколько зон МСК. В связи с этим появилась задача определять зону МСК для каждой точки автоматически с возможностью уточнения зоны пользователем в ручном режиме.
3. Импорт данных из разных форматов:
- kmz, kml (kmz – zip-архив с kml-файлом; kml – xml-разметка пространственных данных, сделанных по стандартам google earth или opengis; изыскатели, строители, проектировщики и кадастровые инженеры часто используют этот формат данных для обмена между различными ГИС и приложениями, в том числе навигационными приемниками типа Garmin);
- asc – формат экспорта данных спутниковых измерений из программного комплекса Leica Geo Office;
- csv – стандартный формат экспорта данных спутниковых измерений из программного комплекса Topcon Magnet Tools;
- txt – стандартный формат экспорта данных спутниковых измерений из программного комплекса Justin (JAVAD);
- xlsx – здесь пользователи хотели иметь возможность простого взаимодействия с таблицами Excel, применяя привычные комбинации клавиш: скопировать целиком весь массив данных из таблицы Excel (Ctrl+C) и сразу же вставить его в сервис пересчета координат (Ctrl+V) без необходимости загрузки самой таблицы Excel в виде файла.
4. Сервис должен обладать базовыми возможностями ГИС:
- свернуть-развернуть карту в полноэкранный режим;
- переключить подложки (схему, спутник, рельеф);
- включить-отключить границы зон МСК в виде полигонов;
- центрировать все данные на карте по их пространственным границам;
- центрировать отдельный объект из таблицы на карте;
- подсветить выделенные объекты из таблицы на карте.
Нам удалось реализовать эти требования в созданном веб-сервисе. При получении координат WGS сервис автоматически определяет номер зоны МСК и далее производит пересчет по заданным параметрам перехода. Все это происходит в онлайн-таблицах, совмещенных с картой. В качестве параметров перехода использовались открытые данные. Реализацию этого решения мы выкладываем в открытый доступ. Веб-сервис находится по ссылке: wgs-msk.solbox.app (рис. 9).
ОЦЕНКА ТОЧНОСТИ ПЕРЕСЧЕТА
Для оценки точности параметров перехода было выбрано 11 объектов, расположенных в разных регионах России. В качестве исходных данных были взяты уравненные результаты измерений, полученные с помощью геодезических GNSS-приемников на пунктах Государственной геодезической сети в системе координат WGS-84, а также каталоги координат для данных пунктов в местных системах координат, полученные в управлениях Росреестра.
В таблице 5 представлены полученные данные по оценке точности параметров перехода. В столбцах под названием «без учета поправки» представлены разности между координатами, полученными по формулам и по каталогам координат. Эти величины зависят от:
- точности получения координат в WGS-84, так как сеть уравнивалась как свободная в зависимости от выбора координат исходного пункта (базового, референцного): полученных из навигации, введенных из каталога или рассчитанных от пунктов сети IGS;
- качества исходной основы, указанной в каталогах координат Росреестра;
- качества непосредственных спутниковых измерений;
- точности модели перехода (параметров перехода).
Для исключения влияния ошибки, связанной с определением координат исходного пункта в системе координат WGS-84, примем данную ошибку равной среднему отклонению разностей координат идентичных пунктов, полученных путем пересчета по модели результатов спутниковых измерений и взятых из каталогов координат Росреестра. Принимая, что координаты пунктов (вычисленные и взятые из каталогов) являются равноточными, среднее отклонение будет являться средним арифметическим значением данных разностей координат. В таблице 5 в столбцах под названием «с учетом поправки» представлены разности координат пунктов, полученных из результатов преобразования с учетом поправки (среднего отклонения с противоположным знаком) и из каталога.
Абсолютная ошибка была рассчитана как сумма разностей по модулю, деленная на количество вероятных достоверных значений. Полученные значения будут зависеть от точности параметров пересчета и исходных данных.
Таблица 5. Оценка точности пересчета
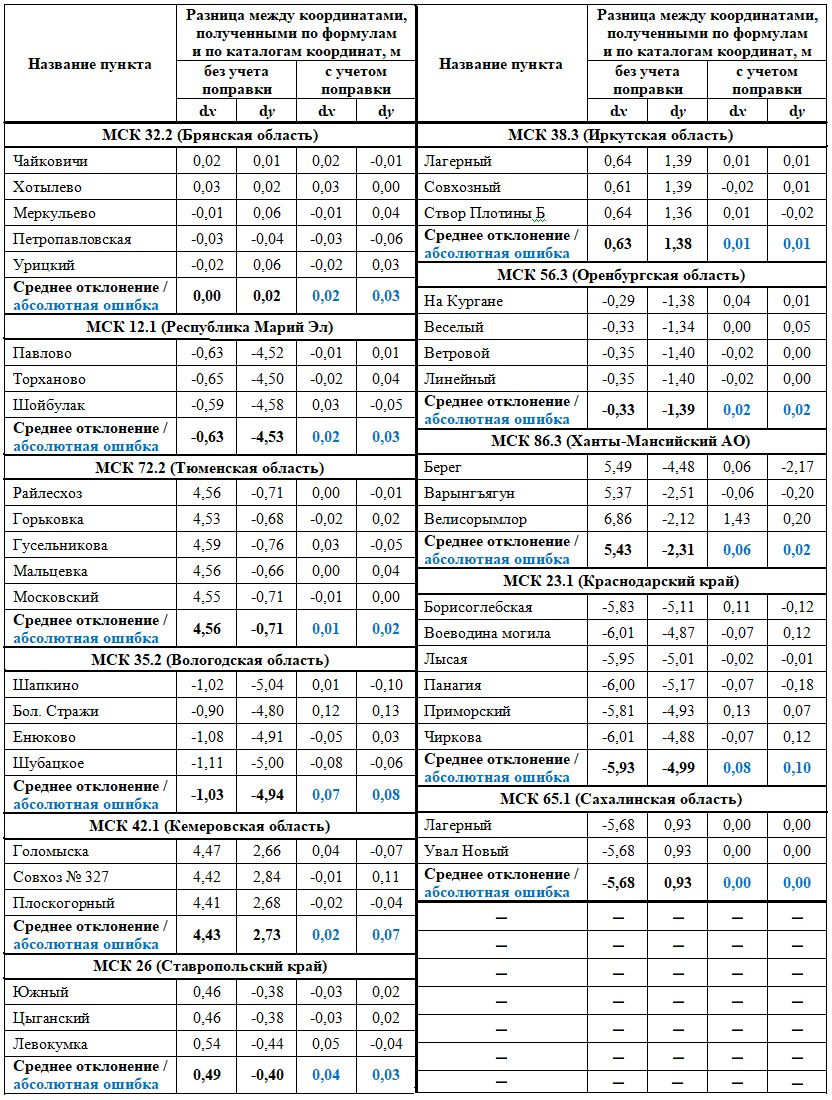
Как следует из данных таблицы 5, полученные отклонения пересчета при исключении ошибки определения координат в системе координат WGS-84 (навигационных координат) находятся в пределах дециметрового диапазона. Таким образом, для повышения точности необходимо делать контрольные измерения на точках с известными координатами в местной системе координат для введения линейной поправки или выполнять измерения от пункта с известными координатами и вводить его координаты как контрольные до начала расчета и уравнивания спутниковой сети. Кроме того, используя данные параметры, можно выполнить оценку качества исходной основы, полученной из каталогов, и сделать отбраковку, так как точность измерений, выполненных с помощью GNSS-приемников в режиме STATIC, в большинстве случаев выше точности исходной сети.
ВЫВОДЫ
В заключение нашего исследования мы хотели бы подчеркнуть, что точность и надежность преобразования координат из глобальных систем в локальные и обратно критически важны для геодезических и картографических приложений. Наша работа над разработкой интерактивного веб-сервиса для преобразования координат нацелена на улучшение пользовательского опыта специалистов для решения этой задачи, особенно для линейных объектов.
Особое внимание в нашем исследовании мы уделили методологии анализа точности и надежности преобразований, поскольку использовали открытые данные в качестве параметров перехода. В результате нам удалось подтвердить дециметровую точность пересчета.
Надеемся, что результаты нашего исследования будут способствовать дальнейшему развитию и улучшению методов работы с геоданными, а также повышению качества пользовательского опыта современных картографических приложений.
Мы благодарны И.И. Яицкому за создание современного интерфейса веб-сервера, А.М. Папсуевой за создание красочных иллюстраций, К.А. Миниханову за помощь в переводе расчетных формул в формализованный код и за подготовку начальных данных, команду Soilbox за разработку сервиса. Также благодарим наших друзей и коллег за участие в обсуждении, критические замечания, предложенные дополнения и тестирование сервиса, без которых наше исследование не было бы полным: В.В. Лощилина (ООО «ГЕОМ»), А.В. Грицая (ООО «Норникель Технические Сервисы»), Р.Ю. Жидкова (ГБУ «Мосгоргеотрест»), Д.С. Савченко (ФГБУ ИГЭ РАН), М.А. Булатникова (МГУ им. М.В. Ломоносова).
Примечание 1. Геоид – это представление физической формы Земли близкое к реальности без учета особенности рельефа, представляющее собой выпуклую, замкнутую поверхность. Эта поверхность приблизительно соответствует среднему уровню вод Мирового океана в состоянии покоя, а также условно продолжается под континентами. При этом в каждой его точке направление силы тяжести перпендикулярно его поверхности.
- Телеганов Н.А., Тетерин Г.Н. Методы и системы координат в геодезии. Новосибирск: Изд-во СГГА, 2008.
- ГОСТ 32453-2017. Глобальная навигационная спутниковая система. Системы координат. Методы преобразований координат определяемых точек. М., 2017
- Клюшин Е.Б., Киселев М.И., Михелев Д.Ш., Фельдман В.Д. Инженерная геодезия. М.: ACADEMA, 2004.
- Дьяков Б.Н. Геодезия. Общий курс. Новосибирск: Изд-во СГГА, 2004.
- Постановление Правительства РФ от 24.11.2016 № 1240 «Об установлении государственных систем координат, государственной системы высот и государственной гравиметрической системы». М., 2016.
- Федеральный закон от 13.07.2015 № 218-ФЗ «О государственной регистрации недвижимости». М., 2015.
- Постановление губернатора Владимирской области от 26.10.2009 № 876 «Об утверждении Положения о местной системе координат Владимирской области (МСК-33)». Владимир, 2009.
- Положение о пространственной местной системе координат города Москвы (ПМСК Москвы). М., 2011.
- Приказ Росреестра от 23.03.2016 № П/0134 «Об утверждении геометрических и физических числовых геодезических параметров государственной геодезической системы координат 2011 года». М., 2016.
- Веб-сайт MapBasic. Дата последнего обращения: 14.01.2024. URL: mapbasic.ru.
ДЛЯ СПРАВКИ
- Бессель Ф.В. Избранные геодезические сочинения / под ред. Г.В. Багратуни, пер. с нем. Н.Ф. Булаевского. М.: Издательство геодезической литературы, 1961. 283 с.
- Закатов П.С. Курс высшей геодезии (4-е изд., перераб. и доп.). М.: Недра, 1976.
- Новое во вращении Земли вокруг своей оси – Леонид Зотов (видео) // НаукаPRO. 14.01.2024. URL: youtube.com/watch?v=-RKhJazHbEo&ysclid=lrtfg9m30988776324.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц















