Сравнение моделей грунта Рамберга – Осгуда и Хардина – Дрневича в программе Midas GTS NX

ВВЕДЕНИЕ

Ответ конструкций на динамическое нагружение напрямую зависит от реакции грунта под ними или вокруг них. Поэтому многие исследователи в последние несколько десятилетий сосредоточили внимание на изучении поведения грунтов, подвергающихся динамическим нагрузкам.

Принято считать, что наиболее важными параметрами, определяющими это поведение, являются динамический модуль сдвига и коэффициент демпфирования (поглощения), от которых зависят изменения жесткости и диссипация энергии при циклическом нагружении. Поэтому, чтобы иметь возможность численно изучить взаимодействия «грунт – конструкция» с достаточной точностью, важно иметь модель материала, которая хорошо отражает поведение грунта в полевых условиях. Это было проблематично, когда речь шла о схемах неравномерного нагружения, из-за сложного поведения грунтов и его зависимости от многих факторов, таких как бытовое давление, коэффициент пористости, плотность, количество циклов и т. д.

Однако прогрессивное развитие компьютерных технологий (в том числе увеличение скорости сложных расчетов при обработке данных) позволило использовать численное моделирование для более простой и быстрой калибровки моделей в целях их дальнейшего использования при решении конкретных и гораздо более сложных геотехнических задач (например, для моделирования фундаментов глубокого заложения [1–2] и тоннелей [3]).

В настоящей статье использовались модели Рамберга – Осгуда (Ramberg-Osgood) и Хардина – Дрневича (Hardin-Drnevich) для имитации и прогнозирования поведения грунта при испытании на чистый сдвиг при кручении (TOrsional Simple Shear – TOSS), то есть методом крутильного сдвига. При этом результаты сравнивались с данными испытаний для случаев неравномерного нагружения.

НЕЛИНЕЙНЫЙ ДИНАМИЧЕСКИЙ МОДУЛЬ СДВИГА

Жесткость грунта при сдвиге обычно выражается модулем сдвига G, который представляет собой наклон кривой зависимости «напряжение – деформация». Его можно определить в полевых условиях с помощью сейсмических методов, чтобы получить скорость поперечных волн in situ, когда уровень деформаций очень низок и грунт все еще ведет себя упруго. Также могут быть использованы уравнения на основе обширных лабораторных испытаний для расчета начального динамического модуля сдвига G_max, который коррелирует с всесторонним давлением, коэффициентом пористости и коэффициентом однородности C_U. Наиболее часто используемые уравнения были представлены Хардином и Ричартом [4], Хардином и Блэком [5] и совсем недавно – Вихтманом, Наваррете-Эрнандесом и Триантафиллидисом [6].

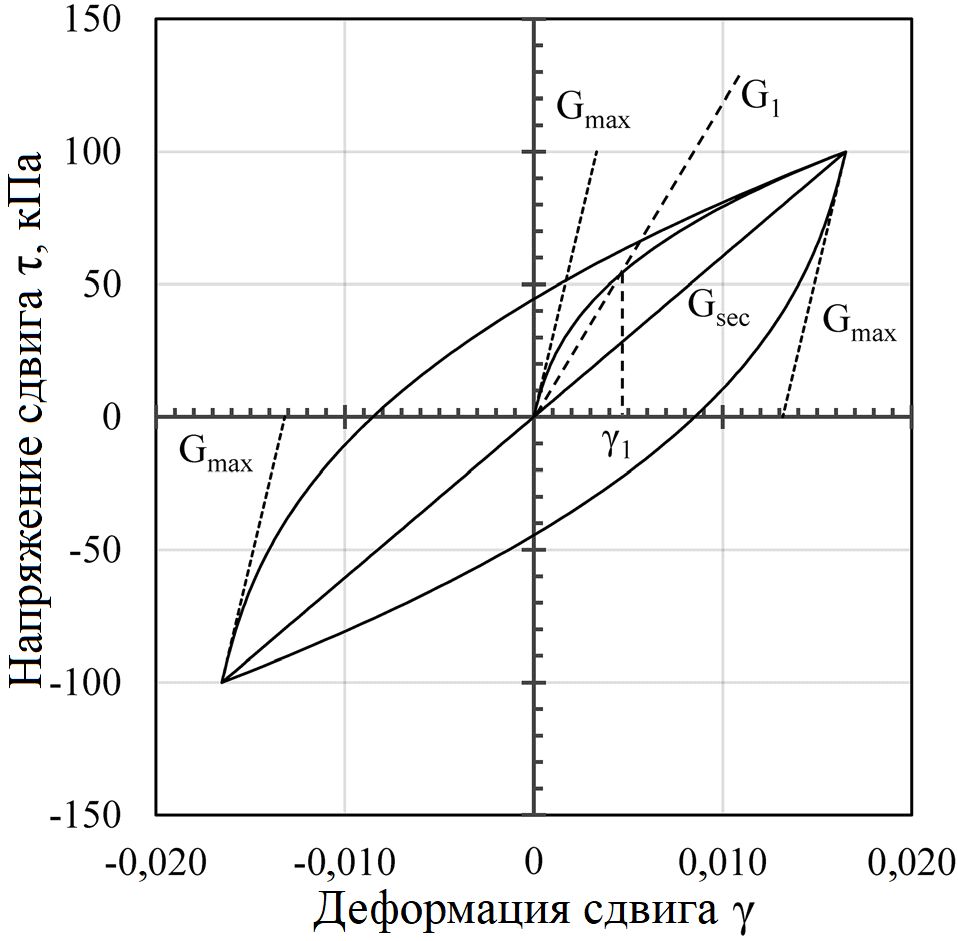
Вучетич и Добри [7] и Ишихара [8] определили пороговую объемную деформацию сдвига в условиях циклического нагружения (γ_tv), при превышении которой идет постоянное необратимое изменение микроструктуры и жесткости дисперсного грунта. Кроме того, модуль сдвига уменьшается по мере увеличения амплитуды деформации сдвига и поведение грунта становится нелинейным. На данном этапе для описания этого свойства обычно используется кривая уменьшения (деградации) модуля сдвига, что важно для анализа различных динамических задач, в которых деформации имеют большие амплитуды (например, при сильных движениях  грунта во время землетрясений). Кривая деградации модуля сдвига может быть получена по результатам испытания на крутильный сдвиг (TOSS), при котором генерируются петли гистерезиса на кривой «напряжение – деформация». По последним вычисляются значения секущего модуля сдвига G_sec при увеличении уровня деформации (рис. 1).

Рис. 1. Оценка модуля сдвига при циклическом нагружении

КОМБИНИРОВАННОЕ ИСПЫТАНИЕ НА РЕЗОНАНСНОЙ КОЛОНКЕ И МЕТОДОМ КРУТИЛЬНОГО СДВИГА

Использованное в данном исследовании комбинированное устройство для испытаний на резонансной колонке и на чистый сдвиг при кручении (RC-TOSS) первоначально было разработано профессором Ричардом Рэем (Richard Ray) в Мичиганском университете в 1980-х годах [9, 10]. В 2013 году оно было модифицировано и откалибровано Жольтом Сильвадьи  в геотехнической лаборатории кафедры геотехники и проектирования зданий и сооружений Университета имени Иштвана Сечени в венгерском городе Дьёр и подробно описано в диссертационной работе этого исследователя [11].

Были проведены испытания при циклическом и при неравномерном нагружении, а также комплекс испытаний сухого песка на резонансной колонке (RC) до уровней напряжения 60 кПа и всестороннего давления 94 кПа. На рисунке 2 вместе с прочими показаны результаты испытания на резонансной колонке, при котором максимальный модуль сдвига составил 95 500 кПа. Другие испытания RC проводились при более высоких напряжениях.

Рис. 2. Сопоставление кривых деградации модуля сдвига

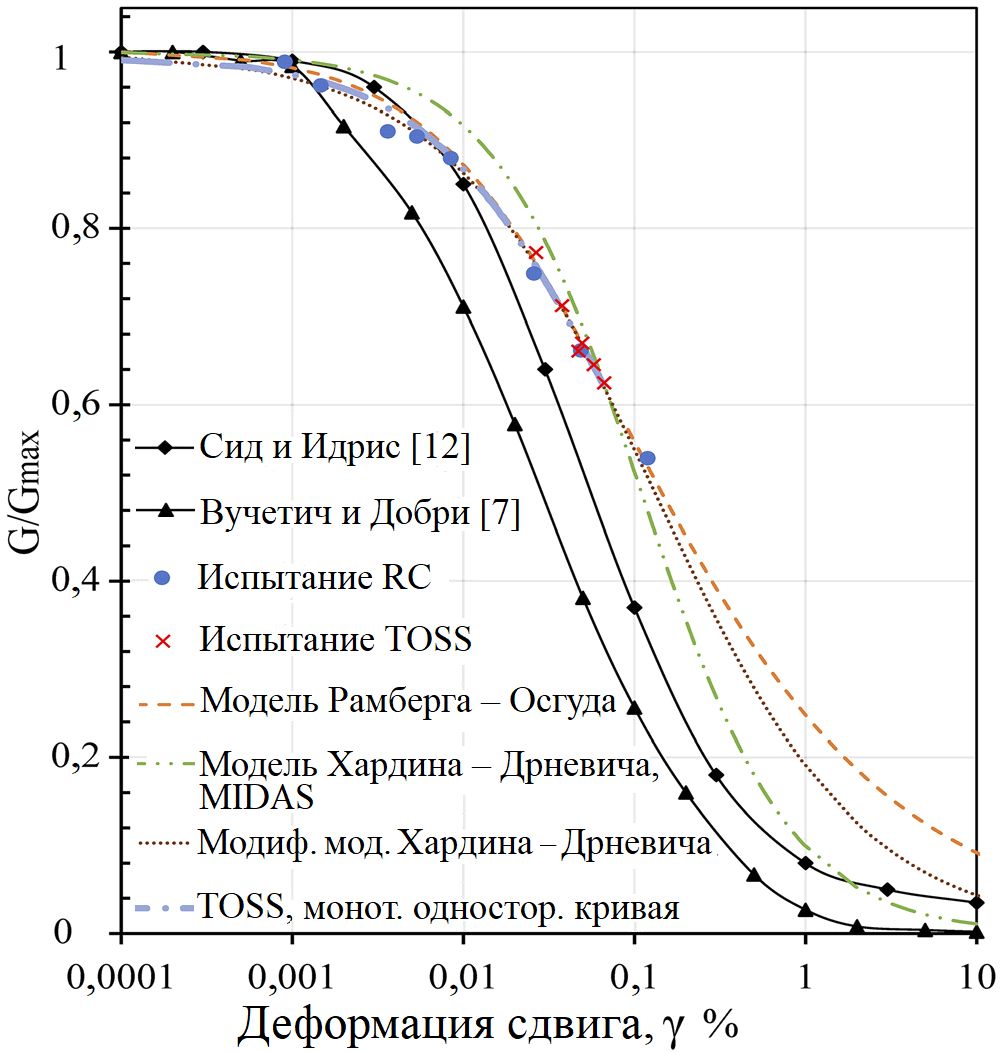
Было выполнено только одно испытание при неравномерном нагружении методом крутильного сдвига (TOSS) при напряжении сдвига 40 кПа для оценки способности моделей материалов предсказывать динамическое поведение дисперсного грунта. История неравномерного нагружения была масштабирована так, чтобы получить максимальное значение напряжения сдвига 40 кПа для этого TOSS с контролируемым напряжением. Полученная зависимость «напряжение – деформация» использовалась для аппроксимации (fitting) соответствующей кривой и калибровки модели. Величины модуля сдвига по данным испытания TOSS были получены по монотонной односторонней (однонаправленной) кривой, а также по значениям секущего модуля сдвига G_sec (наклонам линий, соединяющих два конца каждой из петель).

Из рисунка 2 видна хорошая совместимость результатов испытаний TOSS и RC, а также их схожесть с результатами исследований Сида и Идриса [12] и Вучетича и Добри [7].

МОДЕЛИ МАТЕРИАЛОВ

Модель Рамберга – Осгуда

Рамберг и Осгуд [13] предложили модель с тремя параметрами для описания кривых «напряжение – деформация» для листов (пластин) из алюминиевого сплава, нержавеющей стали и углеродистой стали. Фаччоли и др. [14] использовали ее для моделирования поведения дисперсного грунта с целью прогнозирования кривой деградации модулей сдвига песков. Формула, описывающая нелинейное поведение «напряжение – деформация», для использования в практических расчетах для дисперсных грунтов имеет следующий вид:

С помощью простых манипуляций с уравнением (1) можно также получить формулу для кривой деградации модуля сдвига (а также коэффициент демпфирования, или поглощения):

где γ – относительная деформация сдвига; τ – напряжение сдвига (касательное); G_max – модуль сдвига при малой деформации; τ_max – максимальное напряжение сдвига, обычно получаемое по результатам трехосных испытаний и являющееся функцией всестороннего напряжения, угла внутреннего трения и удельного сцепления; α, C, R – константы для аппроксимации кривой.

Эта модель была модифицирована в соответствии с исходными критериями Мазинга (Masing) [15], поскольку модуль сдвига для кривых на этапе разгрузки и повторного нагружения равен G_max, а по форме эти графики представляют собой односторонние (однонаправленные) кривые, за исключением двукратного увеличения.

Пайк [16] предложил два дополнительных правила для предсказания траекторий этих кривых: кривые разгрузки и повторного нагружения должны соответствовать исходной кривой в случае превышения предыдущей максимальной деформации сдвига; а если кривая текущих нагружения или разгрузки пересекает предыдущую, она должна следовать предыдущей кривой. Эти расширенные правила можно легко запрограммировать, чтобы определить траекторию, по которой будет следовать кривая «напряжение – деформация» для сложных историй нагружения. А исходные правила можно реализовать, модифицировав формулу односторонней (однонаправленной) кривой следующим образом:

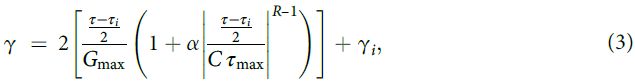
где τ_i, γ_i – соответственно напряжение сдвига (касательное) и относительная деформация сдвига в поворотной точке.

Модифицированная модель Рамберга – Осгуда была реализована в программе Midas GTS для дисперсных грунтов твердой консистенции. Однако следующее уравнение, использованное в этой программе, немного отличается от обычного:

где G₀ = G_max; α, β определяются по формулам:

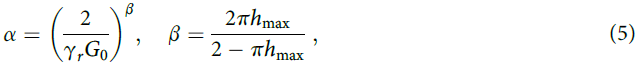
где h_max – максимальная постоянная демпфирования; γ_r – эталонная деформация сдвига.

Для петли гистерезиса также использовались расширенные критерии Мазинга:

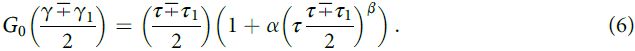
Модель Хардина – Дрневича

Хардин и Дрневич [17] предложили модифицированную гиперболическую зависимость для прогнозирования поведения «напряжение – деформация» при сдвиге для дисперсного грунта. Они обнаружили, что это поведение описывается гиперболой неточно. Поэтому они модифицировали гиперболическое уравнение, исказив масштаб деформации так, чтобы реальная кривая «напряжение – деформация» имела гиперболическую форму. Введенное Хардином и Дрневичем уравнение используется и в программе Midas. Выглядит оно следующим образом:

где G₀ – начальный модуль сдвига; γ_r – эталонная деформация сдвига, которую можно модифицировать так, чтобы получить наилучшее соответствие данным испытаний.

Петли гистерезиса также описываются формулой на основе правила Мазинга:

КОНЕЧНОЭЛЕМЕНТНАЯ МОДЕЛЬ В ПРОГРАММЕ MIDAS GTS

Для этого исследования в программе Midas GTS NX была построена модель на основе статьи Сильвадьи и Рэя [18]. Однако указанная работа [18] была сосредоточена на изучении жесткости дисперсных грунтов при малых деформациях и подтвердила способность Midas GTS NX моделировать испытания методом крутильного сдвига (TOSS) более статическим образом. Кроме того, при анализе Сильвадьи и Рэя возникали некоторые трудности моделирования, которые были преодолены при разработке модели в представляемом сейчас исследовании. Оно было сосредоточено в основном на прогнозировании динамического поведения дисперсных грунтов при неравномерных и более сложных режимах нагружения, что не было учтено в вышеупомянутой работе [18].

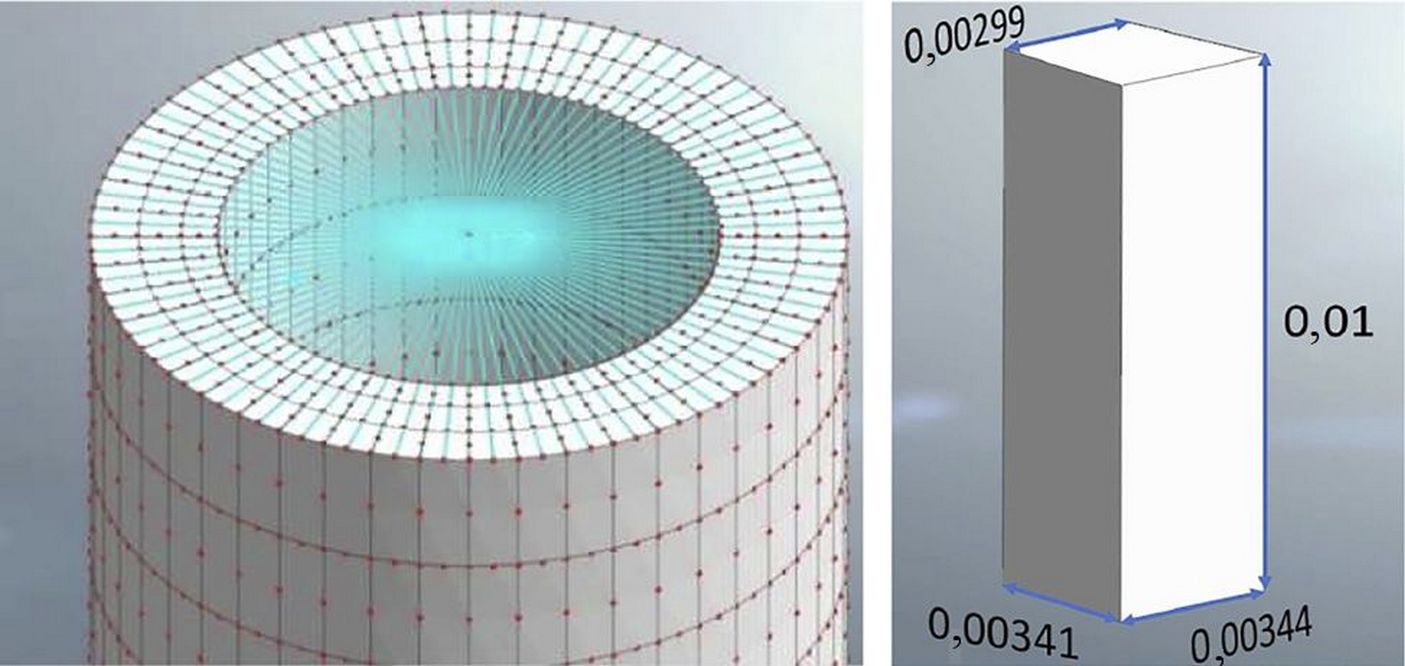
Для настоящей статьи моделирование в Midas GTS NX выполнялось с использованием цилиндрической системы координат. Полученная модель имитирует испытание TOSS, поэтому она представляет собой полый (трубчатый) цилиндр с толщиной стенки 1 см и с теми же размерами, что и у испытываемого образца грунта. В ней использованы шестигранные элементы сетки высокого порядка, каждый из которых имеет 20 узлов (рис. 3, а). Размеры среднего элемента показаны на рисунке 3, б (в метрах).

Рис. 3. Сетка конечных элементов образца дисперсного грунта: а – элементы и узлы; б – размеры среднего элемента (м)

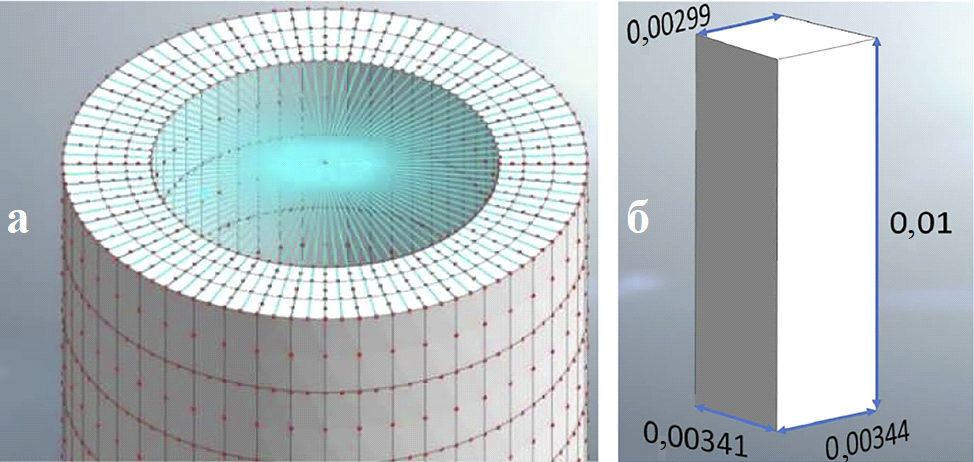
Эта модель состоит из 2017 элементов, она закреплена на нижней поверхности, а все верхние узлы связаны жесткими связями с центральным узлом, который может перемещаться вдоль вертикальной оси и вращаться вокруг нее. Этому центральному узлу предписывается вращение (или момент), что должно имитировать крутильную нагрузку, приложенную при испытании TOSS. Никаких неравномерностей в напряжениях в основании модели после стадии предварительного трехосного сжатия не было замечено.

Такой анализ выполняется на этапах строительства с целью имитации условий испытаний. Он начинается с трехосного сжатия при давлении 94 кПа на свободные поверхности элементов, после чего для всех элементов устанавливается динамическая модель материала (Рамберга – Осгуда или Хардина – Дрневича) и начинается этап приложения скручивающей нагрузки. Предписанному вращению вокруг вертикальной оси была назначена функция, изменяющаяся во времени аналогично истории нагружения при испытании TOSS с максимальным углом поворота 0,00338 рад, который вызовет среднюю деформацию сдвига в направлении θ-Z, равную 0,00067 мм/мм. В отличие от исследования Сильвадьи и Рэя [18] не требовалось ручное пошаговое изменение нагрузки до и после поворотных точек, анализ был непрерывным и сходился без проблем (без большого количества итераций).

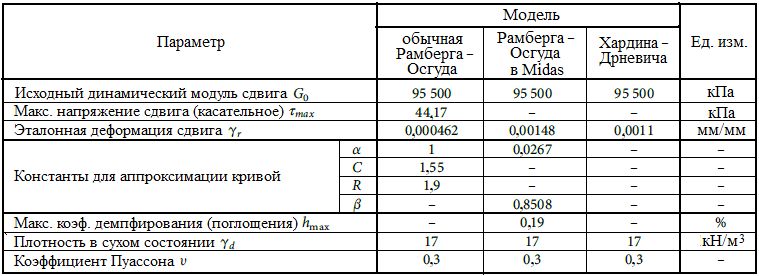
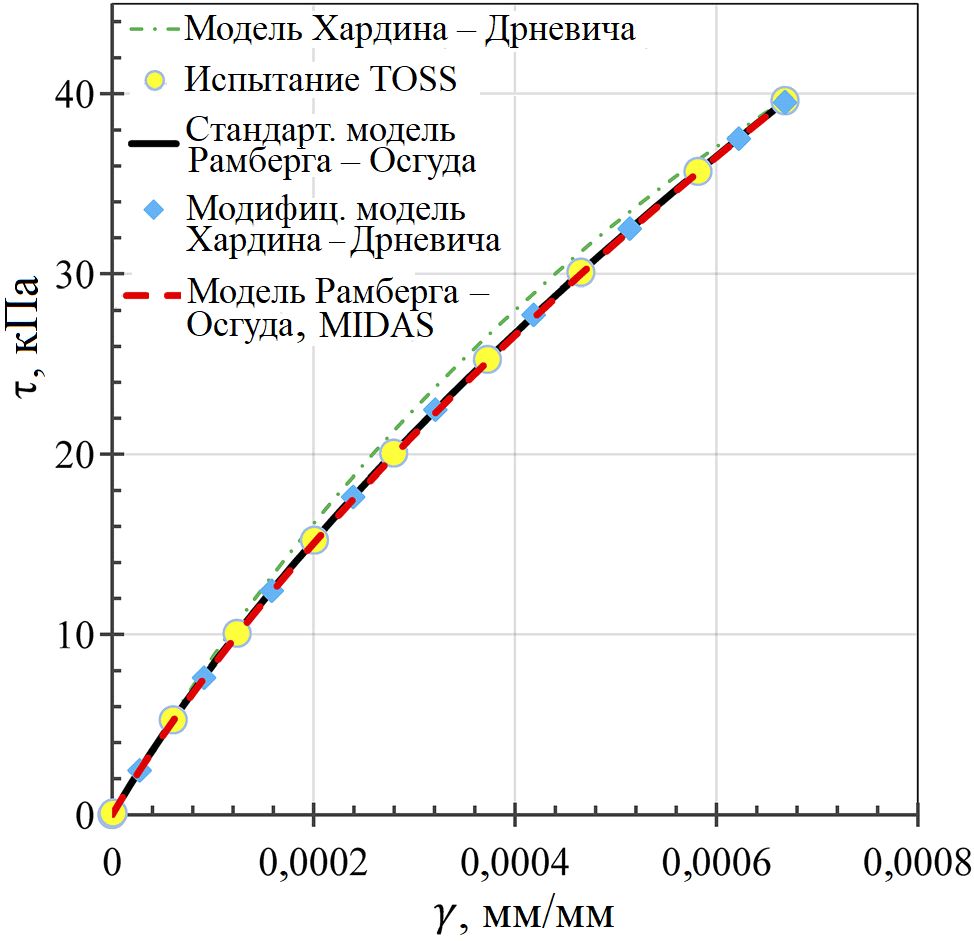
Для нахождения значений постоянной кривизны, которые соответствуют кривым, описываемым уравнениями моделей Рамберга – Осгуда (1) и Хардина – Дрневича на основе данных испытаний (см. таблицу), был использован метод наименьших квадратов с помощью решателя в Excel – путем минимизации суммы квадратов остаточных деформаций (разностей между значением, полученным при испытании, и величиной, подобранной с помощью модели). Тот же метод был применен впоследствии для нахождения эталонной деформации, которая используется в уравнении модели Рамберга – Осгуда в программе Midas (рис. 4).

Таблица. Использованные параметры модели материала

Рис. 4. Аппроксимация кривой для моделей грунта на основе данных испытания методом крутильного сдвига (TOSS)

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ

После первого этапа весь образец подвергается всестороннему давлению (трехосному сжатию)  величиной 94 кПа, в результате чего нормальные напряжения по трем направлениям будут одинаковыми для всех элементов, без заметных отклонений даже при закрепленной нижней поверхности.

Длительность истории нагружения составляет 0,801 секунды с шагом по времени 0,001 секунды, что приводит к 801 временнОму шагу для каждого анализа. На рисунке 5 показано распределение напряжений сдвига (касательных) и деформаций вдоль радиуса образца при конечном приращении. Как и ожидалось, для моделей грунта Рамберга – Осгуда и Хардина – Дрневича результаты наблюдений оказались похожими, поскольку распределение было равномерным по высоте образца и увеличивалось с удалением от центра. Это показывает преимущество использования трубчатого цилиндрического образца для более равномерного распределения напряжений и деформаций вдоль его радиуса.

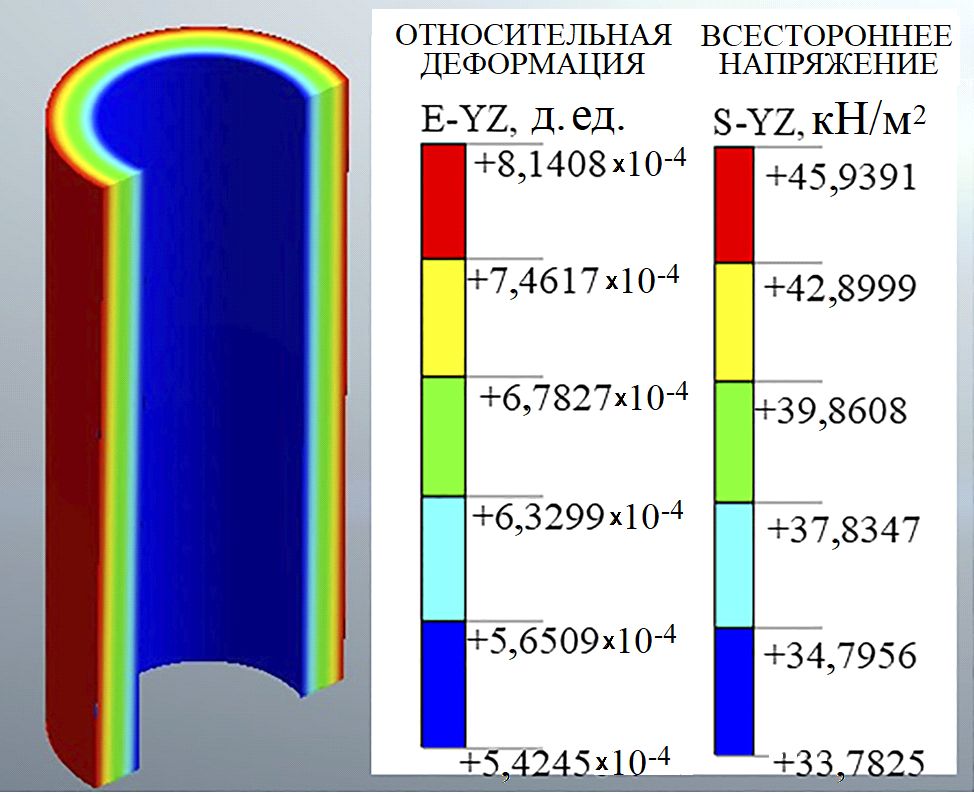
Рис. 5. Распределение по радиусу (при использовании модели Рамберга – Осгуда): а – напряжений сдвига в направлении θ-Z, б – деформаций сдвига в направлении θ-Z

Средние всесторонние напряжения и деформации в направлении θ-Z (S-YZ, E-YZ) для трех типов элементов (внутреннего, среднего и внешнего) в модели сравнивались с кривыми «напряжение – деформация», построенным по результатам испытания методом крутильного сдвига (TOSS) для обеих моделей материалов. Кроме того, по этим кривым рассчитывался динамический модуль сдвига, который также сравнивался с кривыми деградации модуля сдвига, полученными в ходе комбинированных испытаний на резонансной колонке и на крутильный сдвиг (RC-TOSS).

Из рисунка 6 видно очень хорошее соответствие между данными испытаний и кривыми, полученными в результате расчетов методом конечных элементов в программе Midas с применением модели Рамберга – Осгуда. С другой стороны, при использовании модели Хардина – Дрневича с параметрами из приведенной ранее в статье таблицы соответствие было не таким хорошим, как это видно из рисунка 7. А в случае применения обычной гиперболической формулы Хардина – Дрневича (7) расчетные значения еще больше отклонялись от данных испытаний при более высоких уровнях напряжений.

Рис. 6. График «напряжение – деформация», полученный для сдвига в программе Midas с использованием модели Рамберга – Осгуда, в сопоставлении с результатами испытаний методом крутильного сдвига (TOSS)

Рис. 7. График «напряжение – деформация», полученный для сдвига в программе Midas с использованием модели Хардина – Дрневича, в сопоставлении с результатами испытаний методом крутильного сдвига (TOSS)

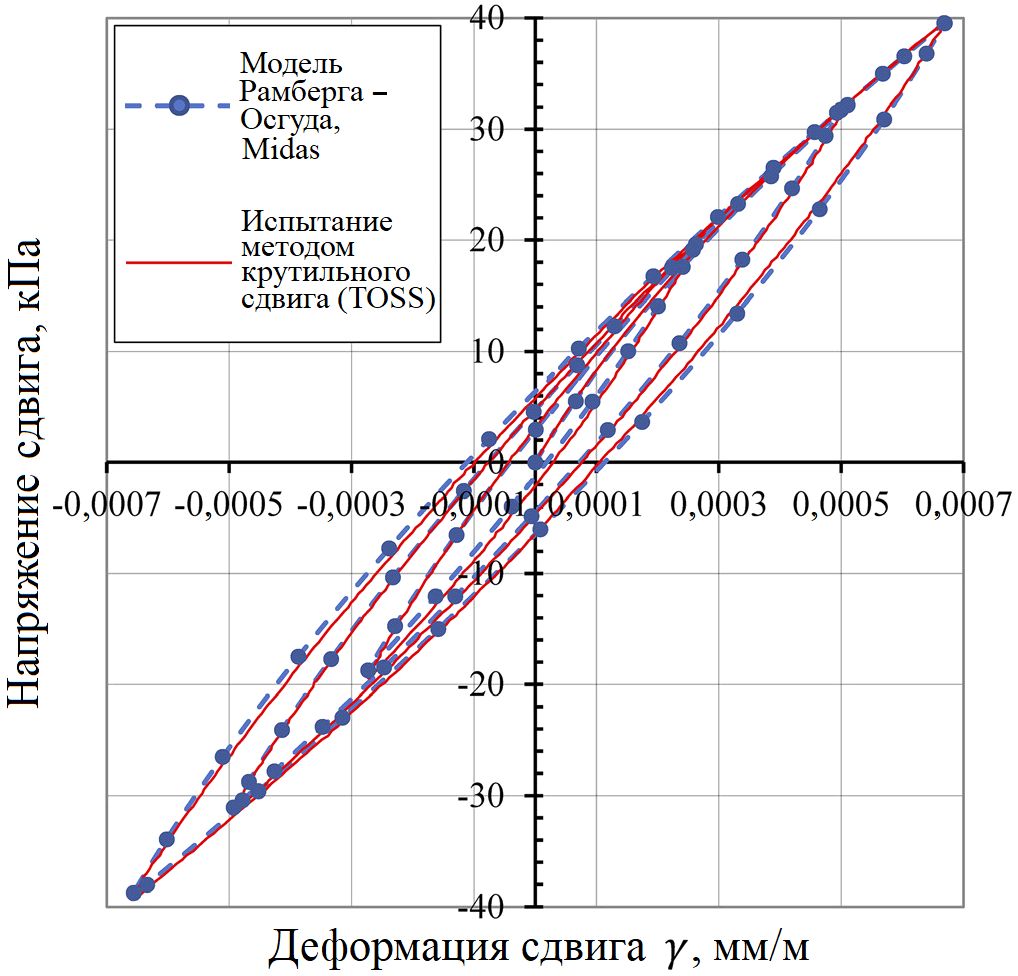
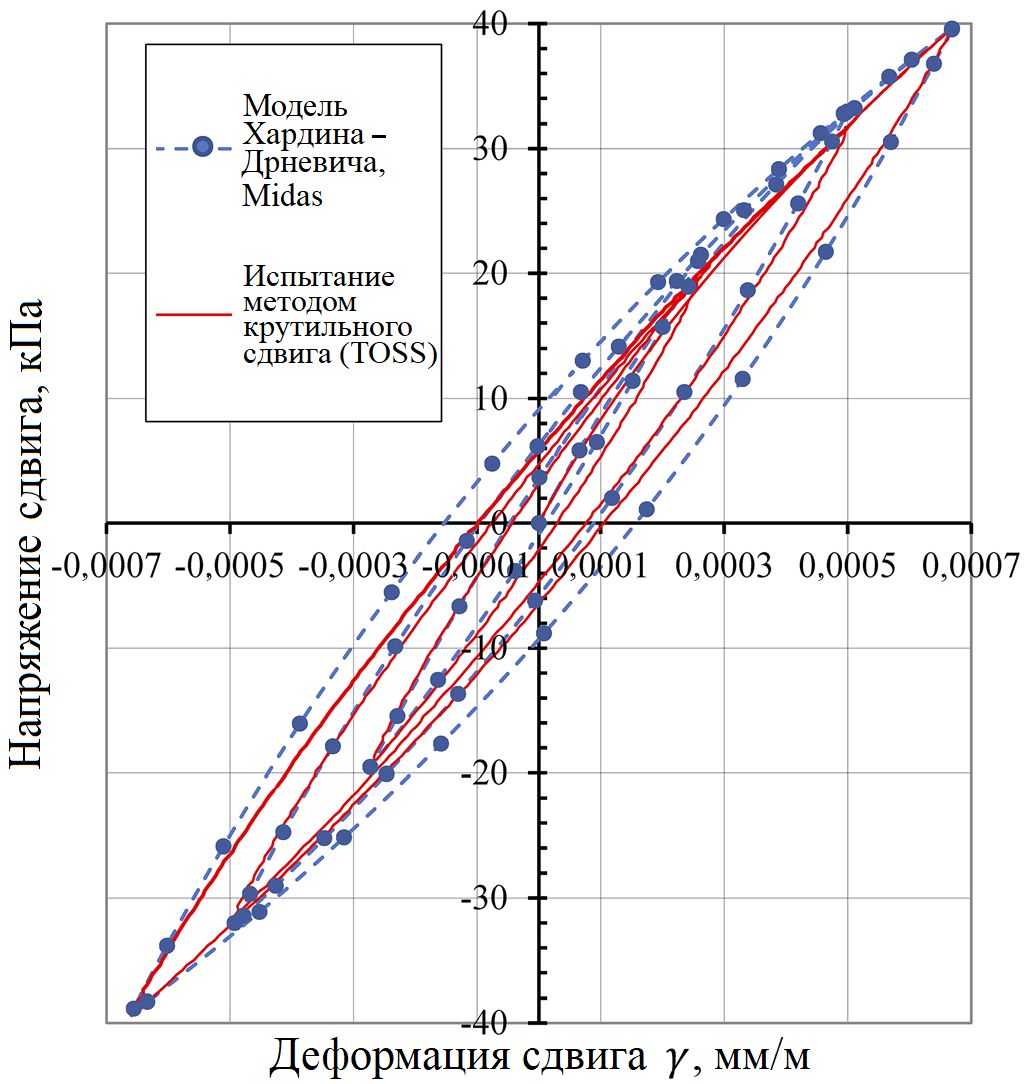
На приведенном ранее рисунке 2 показано, как обе модели предсказывают модуль сдвига при расчетах методом конечных элементов в программе Midas. Кривая деградации модуля сдвига на основе модели Рамберга – Осгуда, рассчитанная по уравнению (2), идеально соответствует результатам расчетов в Midas и очень хорошо согласуется с данными испытаний на резонансной колонке (RC) и на крутильный сдвиг (TOSS). В то время как кривая деградации модуля сдвига, которая была получена на основе монотонной односторонней (однонаправленной) кривой, построенной в результате анализа модели Хардина – Дрневича в Midas, проходит выше реальных значений, пока не достигнет деформации 0,057%, после чего опускается ниже кривой испытания TOSS.

Чтобы достичь лучшего представления кривой уменьшения нормализованного модуля, Дарендели [19] предложил модифицировать гиперболическую модель, введя в уравнение коэффициент формы кривой α (коэффициент кривизны). Такая модификация может быть применена к гиперболическому уравнению Хардина и Дрневича для более хорошего предсказания гистерезисного поведения дисперсных грунтов. В результате получается следующая формула:

При использовании того же метода, что и раньше (метода наименьших квадратов), значения эталонной деформации γ_r = 0,00132 мм/мм и коэффициента кривизны α = 0,7129 дают гораздо более хорошее соответствие с данными испытаний для обеих кривых «напряжение – деформация» (рис. 8) и кривой деградации модуля (см. рис. 2), чем обычная модель Хардина – Дрневича.

Рис. 8. Модель Хардина – Дрневича, модифицированная Дарендели [19], в сопоставлении с результатами испытаний методом крутильного сдвига (TOSS)

ЗАКЛЮЧЕНИЕ

Исследование, представленное в этой статье, было посвящено динамическому поведению грунтов при воздействии неравномерного нагружения.

Были проанализированы результаты испытаний на резонансной колонке (RC) и на чистый сдвиг при кручении (TOSS). Они были использованы в качестве эталонных для оценки способности моделей грунта Рамберга – Осгуда и Хардина – Дрневича прогнозировать кривые «напряжение – деформация» при указанных типах сдвиговых нагрузок.

Для имитации испытаний TOSS была создана модель в конечноэлементной программе Midas GTS NX. При этом были преодолены некоторые трудности, возникавшие при разработке предыдущей подобной модели, с целью обеспечения возможности точно строить более сложные гистерезисные кривые для историй сейсмического нагружения. Было подтверждено, что указанная модель способна отражать условия TOSS, поскольку она дала хорошее соответствие с деградацией модуля сдвига и гистерезисным поведением грунта при реальных испытаниях, особенно для модели материала Рамберга – Осгуда. Модель Хардина – Дрневича неплохо, но похуже соответствовала нелинейности кривых «напряжение – деформация» на основе испытаний. Поэтому для получения более хороших результатов было предложено использовать в конечноэлементном программном обеспечении коэффициент кривизны, введенный в гиперболическое уравнение Хардина и Дрневича.

Разработанная в Midas модель может быть полезным и удобным инструментом для имитации испытаний TOSS в целях изучения историй неравномерного нагружения на основе простого циклического или даже однонаправленного теста и для последующего использования полученных параметров при решении сложных геотехнических задач.