Численное моделирование процесса таяния мерзлого грунта

ВВЕДЕНИЕ

В северных и высокогорных регионах, таких как Цинхай-Тибетское нагорье, имеются большие площади с многолетней мерзлотой (ММ) [1]. Однако связанные с этим гидрологические и экологические сложности усугубляются из-за изменений климата [2-7]. В результате глобального повышения температуры ММ теперь тает быстрее. При этом парниковые газы, такие как углекислый газ и метан, выделяющиеся при таянии многолетней мерзлоты, в свою очередь, усугубляют глобальное потепление [8-10]. И эта тенденция сохранится по крайней мере в обозримые десятилетия [11].

В результате таяния многолетней мерзлоты или перемен в характере сезонного подземного льда могут происходить изменения в распределении поверхностных и подземных вод и, соответственно, в гидрологическом и гидрогеологическом режимах [12–14]. Кроме того, циклы замерзания-оттаивания грунтов также могут влиять на здания и сооружения, построенные на таких территориях [15, 16].

Поэтому ключевой темой для изучения влияния изменений климата на бореальные и высокогорные регионы являются грунты в условиях замерзания и оттаивания [17]. Одно из основных направлений в этом отношении – экспериментальные исследования. Так, Ван с соавторами [18] изучали изменения физико-механических свойств цинхай-тибетской глины в результате циклического замерзания-оттаивания. Чжан с коллегами [19] исследовали изменения температуры и объемного содержания незамерзшей воды в процессе замерзания-оттаивания грунта. Позже Ван и др. [20–22] изучали характеристики трещиноватости и механическое поведение скальных пород в таких условиях. Дэрроу и др. [23] измеряли электрокинетический потенциал (дзета-потенциал) грунтов, обработанных катионами, чтобы выяснить его влияние на подвижность незамерзшей воды. Цао и др. [24] изучали влияние циклических обработок замораживанием-оттаиванием на характеристики трещиноватости песчаника. Чжоу и др. [25] исследовали механическое поведение лёсса под воздействием таких циклов. Хан и др. [26] изучали влияние этих циклических процессов на сдвиговую прочность засоленного грунта. Чжао и др. [27–30] исследовали динамическую прочность мерзлой засоленной сульфатной пылеватой глины при циклическом нагружении. Де Гузман и др. [31] обнаружили, что сдвиговая прочность образцов мерзлого грунта при замерзании-оттаивании снижается на целых 50%. Кроме того, некоторые ученые изучали поведение поверхности раздела «мерзлый грунт – бетон» при сдвиге в таких условиях [32, 33].

Помимо экспериментальных исследований, возможным подходом также является численное моделирование. Линь и др. [34–36] построили поле напряжений в зоне верхней части открытой трещины в моделях одноосного сжатия и сдвига. Ли и др. [37] разработали термогидромеханическую (thermo-hydro-mechanical, THM) модель для исследований механизмов разрушения при замерзании-оттаивании и для разработки соответствующих мер инженерной защиты. Чжао и др. [38–41] создали модели поведения скальных пород в таких условиях с использованием модели THM. Гренье и др. [42] изучали потоки подземных вод и перенос тепла в системах, подвергающихся замораживанию-оттаиванию. Хэ и др. [43] предложили модель температурно-влажностных деформаций мерзлых водонасыщенных грунтов. Принимая во внимание влияние потока воды в пористой среде, вызванное эффектом Соре (Soret) и потенциалом сегрегации (разжижения), на скорость фильтрации и распределение давления воды, Тань и др. [44] разработали термогидравлическую (thermo-hydraulic, TH) модель для строительства высокогорного тоннеля Галун Ла (Galung La tunnel) на Тибете. Амири и др. [45] расширили парадигму теоретической кривой замерзания грунта. Курилик и Ватанабэ [46] обобщили и исследовали совмещенные модели, описывающие перенос тепла и воды в холодных регионах.

Грунты в условиях замерзания-оттаивания изучались и изучаются с различных точек зрения. Однако изменения в состоянии мерзлого грунта невозможно отобразить интуитивно. Поскольку внутреннюю эволюцию этого грунта в процессе таяния трудно наблюдать, для изучения изменений, происходящих при этом в содержании воды, температуре, переносе тепла и давлении, был выбран подход, основанный на численном моделировании. Результаты такого исследования имеют определенную эталонную ценность для последующих экспериментов и соответствующих приложений.

ПОСТРОЕНИЕ МОДЕЛИ

Определение модели

Численное моделирование процесса таяния мерзлого грунта выполнялось с помощью пакета программ Comsol Multiphysics 5.5. При этом были выбраны такие интерфейсы, как Darcy’s law («Закон Дарси») и Heat Transfer in Porous Media («Теплоперенос в пористых средах»).

На рисунке 1 схематично отражена построенная двумерная численная модель. Заполненный пористой средой канал длиной 3 м и шириной 1 м c общим направлением фильтрационного потока слева направо содержит зону со льдом в порах, двумерный профиль которой имеет квадратную форму с длиной стороны 0,333 м (далее будем называть эту зону ледяным включением). Начальная температура данного ледяного включения T_ini равна минус 5 °C. Температура в пористом канале T_inw составляет плюс 5 °C. Движение потока жидкости осуществляется за счет гидравлического градиента (потери напора) ΔH, равного 3% по длине канала.

Рис. 1. Схематичное представление численной модели

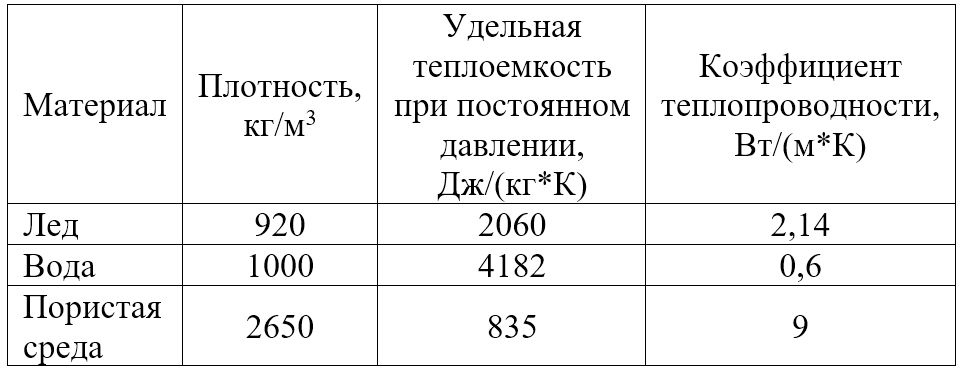
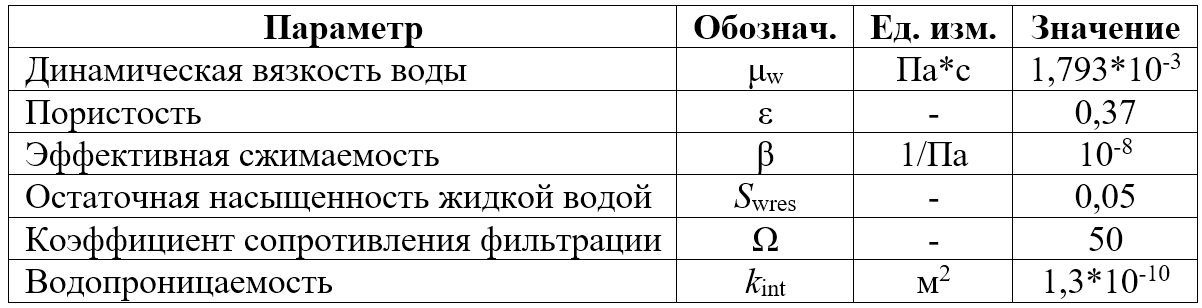
Для облегчения исследовательской работы модель была построена при следующих допущениях: в уравнение теплопереноса не включена термическая дисперсия (рассеяние тепла); плотность воды и динамическая вязкость считаются постоянными по отношению к температуре (таблица 1).

Таблица 1. Свойства льда, воды и пористой среды («скелета », или «твердой матрицы»)

Уравнения модели

При использовании опции Storage model («Модель хранения») в интерфейсе Darcy’s law («Закон Дарси») обеспечивается выполнение закона Дарси, что дает возможность определения линеаризованного хранения S (1/Па) с использованием сжимаемости жидкости и пористой среды («скелета», или «твердой матрицы»):

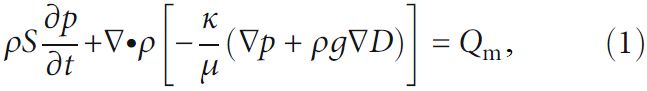
где Q_m – источник массы, который представляет собой дополнительную жидкую воду в результате таяния ледяных включений.

В этом случае S определяется по формуле:

где S_w – водонасыщенность; ε_p – пористость; β – эффективная сжимаемость, которая представляет собой совокупную сжимаемость воды, льда и пористой среды.

Для простоты гравитационной составляющей, имеющейся в уравнении (1), пренебрегают.

В результате формула для определения Q_m выглядит следующим образом:

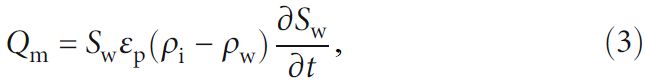
где ρ_i, ρ_w – плотность льда и жидкой воды соответственно.

Водонасыщенность жидкой воды S_w зависит от фазового перехода так:

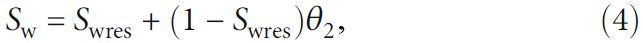
где S_wres – остаточная насыщенность жидкой водой; θ₂ – сглаженная ступенчатая функция, определенная в опции Phase change («Фазовый переход»). Ступенчатая функция θ₂(T) равна нулю для температур ниже температуры плавления T_pc и равна единице для температур выше T_pc.

Теплоперенос в пористой среде описывается следующим уравнением:

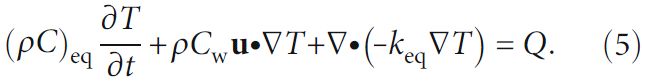
где (ρС)_eq – эквивалентное значение произведения плотности ρ (кг/м³) и удельной теплоемкости при постоянном давлении C (Дж/(кг*К)); k_eq – эффективный коэффициент теплопроводности (Вт/(м*К)); T – температура (К); Q – объемная плотность теплового потока, характеризующая мощность действия внутреннего источника теплоты (Вт/м³); C_w – эффективная теплоемкость жидкости при постоянном давлении (Дж/(кг*К)).

Данные модели

В базовом (контрольном) примере описывается фазовый переход от льда к воде для ледяного включения внутри пористого канала (значения тепловых свойств воды, льда и пористой среды представлены в таблице 1). Применена скрытая теплота плавления L, равная 334 кДж/кг. Дополнительные физические параметры, использованные в примере, сведены в таблицу 2.

Таблица 2. Дополнительные физические параметры

ПОЛУЧЕННЫЕ РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ

Моделирование соответствовало по времени 56 часам. Через 19,2 часа лед полностью растаял, но минимальная температура в пористом канале не возвращалась к первоначальным 5 °C до 56-го часа. При таянии льда изменения различных физических показателей в этом канале могут отражать внутреннюю эволюцию процесса таяния в мерзлом грунте, что заслуживает дальнейшего обсуждения.

Кривые по результатам численного моделирования

В «запущенной» модели лед в грунте постепенно таял и общий объем жидкой воды в пористом канале увеличивался (рис. 2). Примерно через 19,2 ч этот объем вырос до 1,11 м³ и далее оставался постоянным, что свидетельствовало о том, что лед полностью растаял.

Рис. 2. Изменения общего объема жидкой воды в пористом канале в процессе таяния ледяного включения

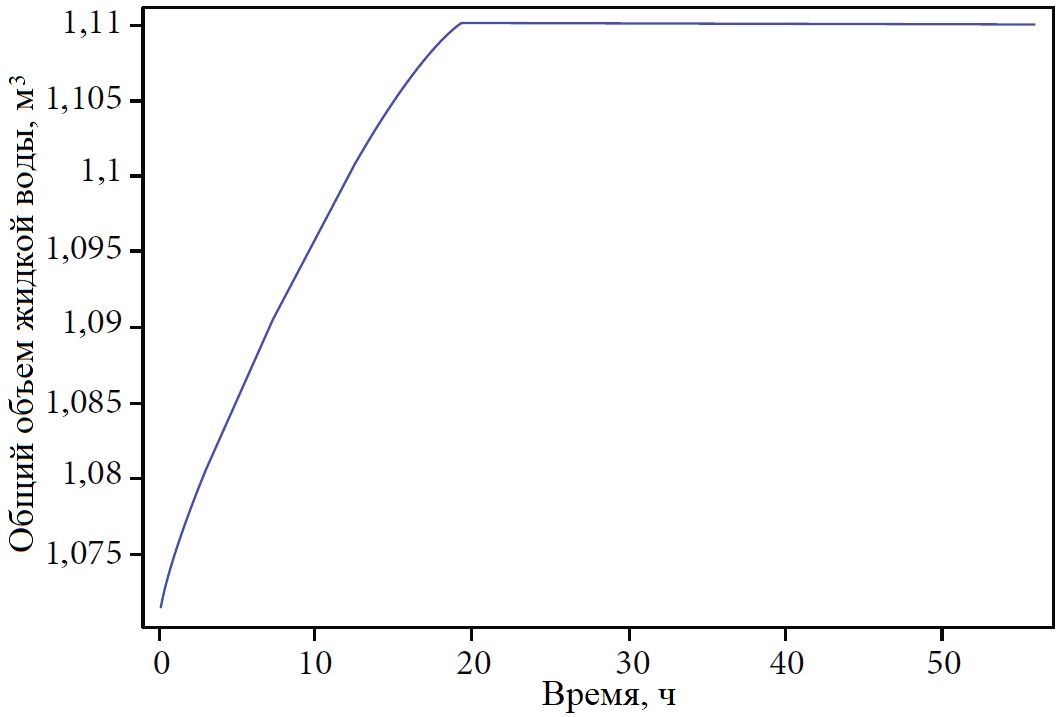
В начале моделирования температура грунта в основной части пористого канала составляла плюс 5 °C, а температура льда – минус 5 °C, в то же время минимальная температура в канале была равна температуре льда, то есть минус 5 °C. Через 56 часов минимальная температура во всем канале стала равной плюс 5 °C.

Как видно из рисунка 3, минимальная температура в канале быстро поднялась до минус 1 °C в течение первых двух часов после начала таяния льда. С момента 2 ч до примерно 19,2 ч она повышалась очень медленно. В узком интервале с 19,2 до 19,9 ч она повышалась быстро и превысила точку замерзания. Затем повышение минимальной температуры в канале происходило в три этапа (медленный, быстрый и опять медленный) и через 56 ч она стала равной плюс 5 °C, какой была исходно в основной части канала.

Рис. 3. Изменения минимальной температуры в пористом канале в процессе таяния ледяного включения

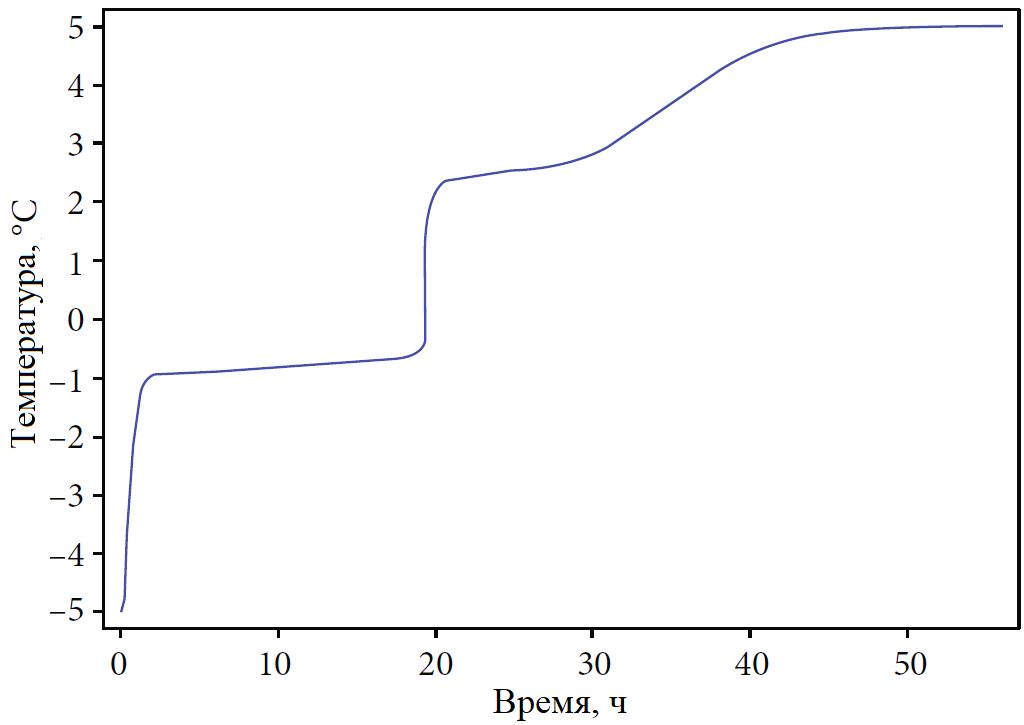
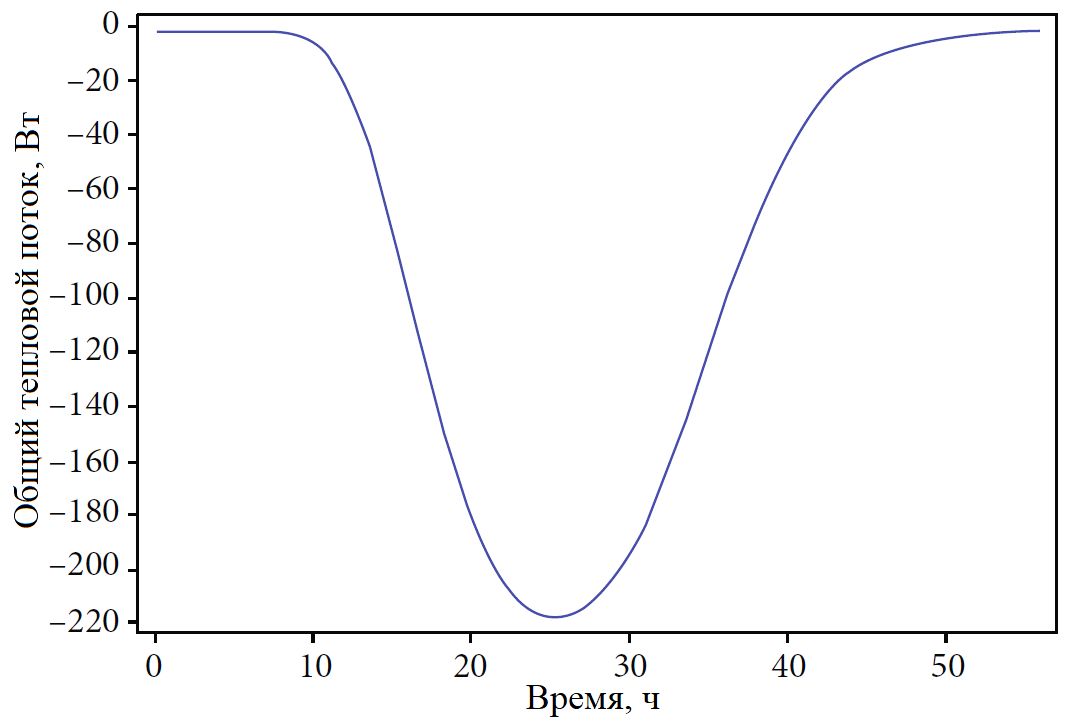
В модели жидкость течет в канале слева направо, поэтому правая сторона очерчивающего его прямоугольника является выходной границей системы (см. рис. 1). Изменения общего теплового потока, выходящего через нее, показаны на рисунке 4. Поскольку ледяное включение находится в левой половине канала на определенном расстоянии от правой границы, тепловой поток , идущий через нее, не соответствует в точности изменениям теплоты, вызванным таянием льда. Поэтому рисунки 3 и 4 не согласуются друг с другом со всей очевидностью (соответствующая взаимосвязь между изменениями теплового потока и температуры будет описана в статье позже). Изменения теплового потока на выходной границе системы обусловлены таянием льда, и этот поток отрицателен по направлению. Но по модулю общий тепловой поток на выходной границе сначала увеличивался, а затем уменьшался (см. рис. 4).

Рис. 4. Изменения общего теплового потока, выходящего из системы через выходную границу канала, в процессе таяния ледяного включения

Распределение жидкой воды

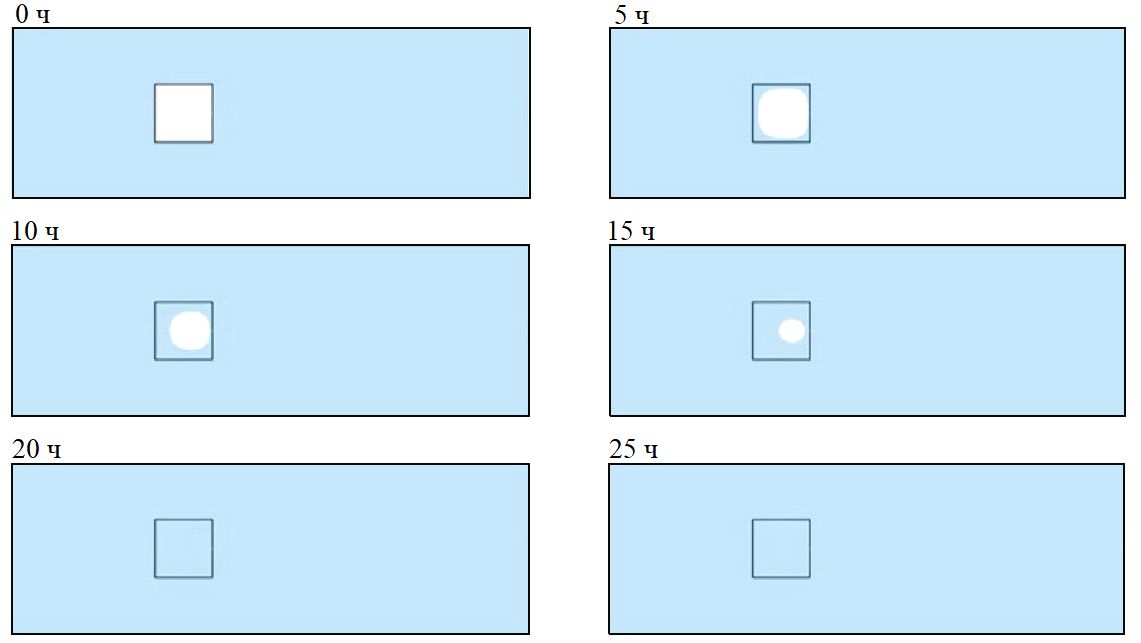
Модельные изменения в распределении жидкой воды в пористом канале показаны на рисунке 5. Видно, что ледяное включение начинает таять с четырех углов. Его левая сторона обращена навстречу к потоку жидкости, и скорость таяния льда слева выше, чем справа. В процессе оттаивания форма профиля включения постепенно меняется с квадратной на круглую и его размеры постепенно уменьшаются вплоть до полного исчезновения льда. Для показанных на рисунке 5 моментов времени видно, что через 20 ч лед полностью растаял, жидкая вода полностью заполнила поры канала, а ее общий объем постоянен (в соответствии с кривой, показанной на рисунке 2).

Рис. 5. Насыщение пористого канала жидкой водой. Зоны с жидкой водой показаны голубым цветом, зоны со льдом – белым

Распределение температуры

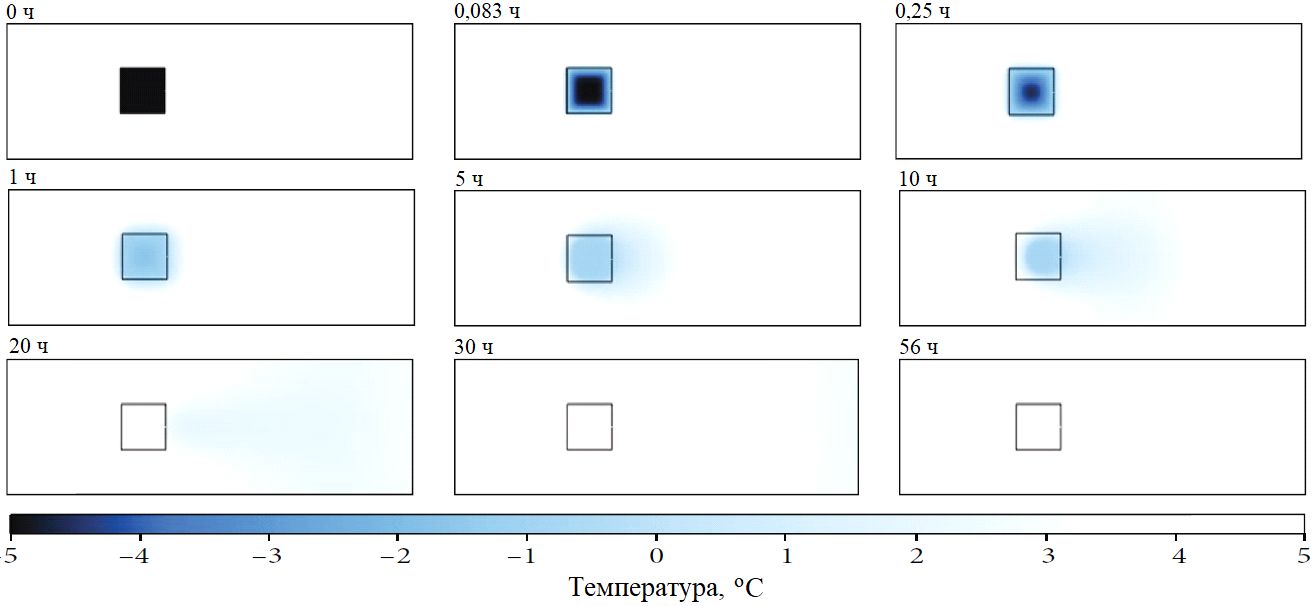
Распределение температуры в пористом канале тоже менялось по мере таяния льда (рис. 6). Зона с температурой ниже 0 °C содержала в порах лед. При таянии льда низкая температура распространялась вокруг его зоны, а затем перемещалась в модели вправо по мере течения жидкости. Наконец низкая температура «вытекла» из канала и в нем везде восстановились первоначальные плюс 5 °C.

На рисунке 6 видно, что в диапазоне времени от 0 до 20 ч распределение льда в процессе его таяния согласуется с рисунком 5. Картины для моментов времени 0; 0,083; 0,25; 1 ч (см. рис. 6) подтверждают быстрое повышение минимальной температуры в пористом канале в течение первого часа моделирования, отраженное на рисунке 3. Таяние льда привело к понижению температуры воды вокруг его зоны. Эта низкотемпературная вода потекла вправо под действием гидравлического напора, что изменило тепловой поток на выходной границе, и это подтверждает показанное на рисунке 4. На рисунке 6 видна выделенная голубым цветом низкотемпературная вода, проходящая через выходную границу в период времени между 20 и 30 ч, что соответствует большим значениям теплового потока по модулю, отраженным на рисунке 4.

Рис. 6. Изменения в распределении температуры в пористом канале в процессе таяния ледяного включения

Распределение давления

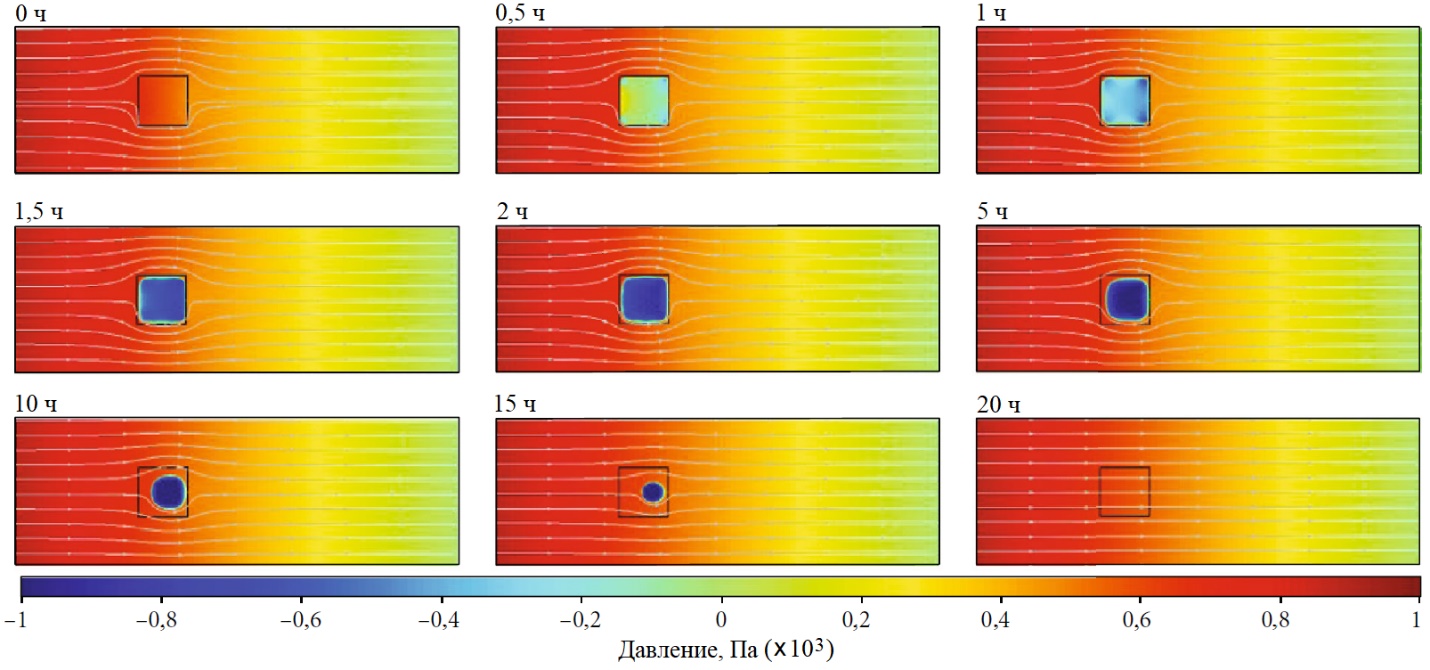
Изменения в распределении давления в пористом канале по мере таяния льда показаны на рисунке 7 в соответствии с цветовой шкалой. Видно, что они сосредоточены в основном в зоне ледяного включения. Светлые линии на рисунке, идущие слева направо, отражают поле скоростей фильтрации (скоростей Дарси) и пути течения жидкости в пористой среде. С началом таяния давление в ледяной зоне стало снижаться. Сначала оно изменилось с положительного на отрицательное в четырех углах включения, а затем полностью стало отрицательным во всей ледяной зоне. Профиль льда в процессе таяния становился все меньше и меньше по площади, потом стал круглым. При этом отрицательное давление постепенно увеличивалось по модулю. В конце концов ледяное включение растаяло полностью, в результате чего величины давления стали одинаковыми в каждом поперечном сечении канала, а линии тока жидкости, поначалу огибавшие включение, заняли зону растаявшего льда и выпрямились.

Рис. 7. Изменения в распределении давления в пористом канале в процессе таяния ледяного включения

ВЫВОДЫ

Для анализа процесса таяния мерзлого грунта была создана двумерная модель сопряженного воздействия «вода – тепло» на таяние ледяного включения в канале, заполненном пористой средой.

Выполненное численное моделирование позволило выявить внутреннюю эволюцию мерзлого грунта в процессе таяния под действием четырех факторов – воды, температуры, тепла и давления. На основе полученных результатов можно сделать следующие выводы.

1. Смоделированные изменения в распределении жидкой воды в процессе таяния мерзлого грунта соответствуют кривой общего объема жидкости и могут отразить площадь профиля нерастаявшего льда.

2. Смоделированные изменения в распределении температуры в процессе таяния мерзлого грунта, с одной стороны, объясняют ход кривой минимальной температуры в пористом канале, а с другой стороны, говорят о том, что минимальная температура воды, проходящей через выходную границу системы, соответствует общему тепловому потоку.

3. Смоделированные изменения давления и путей тока воды показали, что лед в мерзлом грунте в процессе таяния создает отрицательное давление.

4. Выполненное численное моделирование имеет «справочное» значение, поэтому необходимо провести дополнительные полевые наблюдения и исследования по таянию многолетней мерзлоты, чтобы можно было четко понять реальный механизм этого процесса. Одним из возможных подходов является крупномасштабное размещение датчиков в многолетнемерзлых грунтах для мониторинга изменений в процессе оттаивания.

-

Эта работа была выполнена при поддержке Национальной программы ключевых исследований и разработок Китая (грант № 2018YFC0808404).

ИСТОЧНИК ДЛЯ ПЕРЕВОДА

Yan Zh., Pan W., Fang J., Liu Z. Numerical simulation of thawing process in frozen soil // Geofluids. Hindawi, 2020. Article ID 8822320. DOI: doi.org/10.1155/2020/8822320. URL: hindawi.com/journals/geofluids/2020/8822320.

СПИСОК ЛИТЕРАТУРЫ, ИСПОЛЬЗОВАННОЙ АВТОРАМИ ПЕРЕВЕДЕННОЙ СТАТЬИ

1. Xia K., Luo Y., Li W.P. Simulation of freezing and melting of soil on the northeast Tibetan Plateau // Chinese Science Bulletin. 2011. Vol. 56. № 20. P. 2145–2155.
2. Rouse W.R., Douglas M.S.V., Hecky R.E., et al. Effects of climate change on the freshwaters of arctic and subarctic north America // Hydrological Processes. 1997. Vol. 11. № 8. P. 873–902.
3. Serreze M.C., Walsh J.E., Chapin F.S., et al. Observational evidence of recent change in the northern high-latitude environment // Climatic Change. 2000. Vol. 46. № 1/2. P. 159–207.
4. Jorgenson M.T., Racine C.H., Walters J.C., Osterkamp T.E. Permafrost degradation and ecological changes associated with a warming climate in Central Alaska [J] // Climatic Change. 2001. Vol. 48. № 4. P. 551–579.
5. Hinzman L.D., Bettez N.D., Bolton W.R., et al. Evidence and implications of recent climate change in northern Alaska and other Arctic regions // Climatic Change. 2005. Vol. 72. № 3. P. 251–298.
6. Schindler D.W., Smol J.P. Cumulative effects of climate warming and other human activities on freshwaters of arctic and subarctic north America // Ambio. 2006. Vol. 35. № 4. P. 160–168.
7. Zhongqiong Z., Qingbai W., Guanli J., Siru G., Ji C., Yongzhi L. Changes in the permafrost temperatures from 2003 to 2015 in the Qinghai-Tibet Plateau // Cold Regions Science and Technology. 2020. Vol. 169. Article 102904.
8. Anisimov A.O. Potential feedback of thawing permafrost to the global climate system through methane emission // Environmental Research Letters. 2017. Vol. 2. № 4. |Article 045016.
9. Masyagina O.V., Menyailo O.V. The impact of permafrost on carbon dioxide and methane fluxes in Siberia: a meta-analysis // Environmental Research. 2020. Vol. 182. Article 109096.
10. IPCC. Climate change 2001 – the scientific basis // KSCE Journal of Civil Engineering. 2001. Vol. 19. № 2. P. 359–365.
11. IPCC, Stocker T., Qin D., et al. The physical science basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change // Climate Change. 2013. Vol. 2013.
12. Connon R.F., Quinton W.L., Craig J.R., Hayashi M. Changing hydrologic connectivity due to permafrost thaw in the lower Liard River valley, NWT, Canada // Hydrological Processes. 2014. Vol. 28. № 14. P. 4163–4178.
13. Kurylyk B.L., Macquarrie K.T.B., Mckenzie J.M. Climate change impacts on groundwater and soil temperatures in cold and temperate regions: implications, mathematical theory, and emerging simulation tools // Earth-Science Reviews. 2014. Vol. 138. P. 313–334.
14. Frampton A., Destouni G. Impact of degrading permafrost on subsurface solute transport pathways and travel times // Water Resources Research. 2015. Vol. 51. № 9. P. 7680–7701.
15. Yang B., Qin Z., Zhou Q., Li H., Li L., Yang X. Pavement damage behavior of urban roads in seasonally frozen saline ground regions // Cold Regions Science and Technology. 2020. Vol. 174. Article 103035.
16. Yang Z., Dutta U., Xiong F., Biswas N., Benz H. Seasonal frost effects on the dynamic behavior of a twenty-story office building // Cold Regions Science and Technology. 2008. Vol. 51. № 1. P. 76–84.
17. Lawrence D.M., Slater A.G., Swenson S.C. Simulation of present-day and future permafrost and seasonally frozen ground conditions in CCSM4 // Journal of Climate. 2012. Vol. 25. № 7. P. 2207–2225.
18. Wang D.Y., Ma W., Chang X.X., Sun Z.Z., Feng W.J., Zhang J.W. Physico-mechanical properties changes of Qinghai-Tibet clay due to cyclic freezing and thawing // Chinese Journal of Rock Mechanics and Engineering. 2005. Vol. 23. P. 4313–4319.
19. Zhang M., Zhang X., Lai Y., Lu J., Wang C. Variations of the temperatures and volumetric unfrozen water contents of fine-grained soils during a freezing-thawing process //Acta Geotechnica. 2020. Vol. 15. № 3. P. 595–601.
20. Wang Y., Zhang H., Lin H., Zhao Y., Li X., Liu Y. Mechanical behavior and failure analysis of fracture-filled gneissic granite // Theoretical and Applied Fracture Mechanics. 2020. Vol. 108. Article 102674,
21. Wang Y., Lin H., Zhao Y., Li X., Guo P., Liu Y. Analysis of fracturing characteristics of unconfined rock plate under edge-on impact loading // European Journal of Environmental & Civil Engineering. 2019. P. 1–16.
22. Wang Y., Zhang H., Lin H., Zhao Y., Liu Y. Fracture behavior of central-flawed rock plate under uniaxial compression // Theoretical and Applied Fracture Mechanics. 2020. Vol. 106. Article 102503.
23. Darrow M.M., Guo R., Trainor T.P. Zeta potential of cation-treated soils and its implication on unfrozen water mobility // Cold Regions Science and Technology. 2020. Vol. 173. Article 103029.
24. Cao R.-H., Wang C., Yao R., et al. Effects of cyclic freeze-thaw treatments on the fracture characteristics of sandstone under different fracture modes: laboratory testing // Theoretical and Applied Fracture Mechanics. 2020. Vol. 109. Article 102738.
25. Zhou Z., Ma W., Zhang S., Mu Y., Li G. Effect of freezethaw cycles in mechanical behaviors of frozen loess // Cold Regions Science and Technology. 2018. Vol. 146. P. 9–18.
26. Han Y., Wang Q., Wang N., et al. Effect of freeze-thaw cycles on shear strength of saline soil // Cold Regions Science and Technology. 2018. Vol. 154. P. 42–53.
27. Zhao Y., Lai Y., Zhang J., Liao M. A dynamic strength criterion for frozen sulfate saline silty clay under cyclic loading // Cold Regions Science and Technology. 2020. Vol. 173. Article 103026.
28. Zhao Y., Zhang L., Wang W., Tang J., Lin H., Wan W. Transient pulse test and morphological analysis of single rock fractures // International Journal of Rock Mechanics and Mining Sciences. 2017. Vol. 91. P. 139–154.
29. Zhao Y., Zhang L., Wang W., Liu Q., Tang L., Cheng G. Experimental study on shear behavior and a revised shear strength model for infilled rock joints // International Journal of Geomechanics. 2020. Vol. 20. № 9. Article 04020141.
30. Wang C., Zhao Yu., Zhao Ya., Wan W. Study on the interaction of collinear cracks and wing cracks and cracking behavior of rock under uniaxial compression // Advances in Civil Engineering. 2018. № 5. P. 1–10.
31. De Guzman E.M.B., Stafford D., Alfaro M.C., Dore G., Arenson L.U. Large-scale direct shear testing of compacted frozen soil under freezing and thawing conditions // Cold Regions Science and Technology. 2018. Vol. 151. P. 138–147.
32. He P. Mu Y., Yang Z., Ma W., Dong J., Huang Y. Freeze-thaw cycling impact on the shear behavior of frozen soil-concrete interface // Cold Regions Science and Technology. 2020. Vol. 173. № 1. Article 103024.
33. Liu J., Lv P., Cui Y., Liu J. Experimental study on direct shear behavior of frozen soil-concrete interface // Cold Regions Science and Technology. 2014. Vol. 104-105. P. 1 –6.
34. Lin H., Yang H., Wang Y., Zhao Y., Cao R. Determination of the stress field and crack initiation angle of an open flaw tip under uniaxial compression // Theoretical and Applied Fracture Mechanics. 2019. Vol. 104. Article 102358.
35. Xie S., Lin H., Wang Y., et al. A statistical damage constitutive model considering whole joint shear deformation // International Journal of Damage Mechanics. 2020. Vol. 29. № 6. P. 988–1008.
36. Lin H., Zhang X., Wang Y., et al. Improved nonlinear Nishihara shear creep model with variable parameters for rock-like Materials // Advances in Civil Engineering. 2020. Vol. 3. P. 1–15.
37. Li G., Li N., Bai Y., Liu N., He M., Yang M. A novel simple practical thermal-hydraulic-mechanical (THM) coupling model with water-ice phase change // Computers and Geotechnics. 2020. Vol. 118. Article 103357.
38. Zhao Y.L., Wang W.J., Zhao Y.S., Gao W.H. 3D dual medium model of thermal-hydro-mechanical coupling and its application // Journal of China University of Mining & Technology. 2010. Vol. 39. № 5. P. 709–715.
39. Zhao Y., Wang Y., Wang W., Tang L., Liu Q., Cheng G. Modeling of rheological fracture behavior of rock cracks subjected to hydraulic pressure and far field stresses // Theoretical and Applied Fracture Mechanics. 2019. Vol. 101. P. 59–66.
40. Zhao Y., Wang Y., Wang W., Wan W., Tang J. Modeling of non-linear rheological behavior of hard rock using triaxial rheological experiment // International Journal of Rock Mechanics and Mining Sciences. 2017. Vol. 93. P. 66–75.
41. Zhao Y., Zhang L., Wang W., Wan W., Ma W. Separation of elastoviscoplastic strains of rock and a nonlinear creep model // International Journal of Geomechanics. 2018. Vol. 18. № 1. P. 18.
42. Grenier C., Anbergen H., Bense V., et al. Groundwater flow and heat transport for systems undergoing freeze-thaw: intercomparison of numerical simulators for 2D test cases // Advances in Water Resources. 2018. Vol. 114. P. 196–218.
43. He M., Li N., Liu N.F. Analysis and validation of coupled heat-moisture-deformation model for saturated frozen soils // Chinese Journal of Geotechnical Engineering. 2012. Vol. 34. № 10. P. 1858–1865.
44. Tan X., Chen W., Tian H., Cao J. Water flow and heat transport including ice/water phase change in porous media: numerical simulation and application // Cold Regions Science and Technology. 2011. Vol. 68. № 1-2. P. 74–84.
45. Amiri E.A., Craig J.R., Kurylyk B.L. A theoretical extension of the soil freezing curve paradigm // Advances in Water Resources. 2018. Vol. 111. P. 319–328.
46. Kurylyk B.L., Watanabe K. The mathematical representation of freezing and thawing processes in variably-saturated, non-deformable soils // Advances in Water Resources. 2013. Vol. 60. P. 160–177.