Исследования озерных глин с использованием самозабуривающегося прессиометра на озере Тайху (Китай). Часть 4
 Ван Бинь (Wang Bin)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов (г. Ухань) и Университет Китайской академии наук (г. Пекин), Китайbwang@whrsm.ac.cn
Ван Бинь (Wang Bin)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов (г. Ухань) и Университет Китайской академии наук (г. Пекин), Китайbwang@whrsm.ac.cn Лю Кан (Liu Kang)Колледж гражданского строительства при Технологическом университете Хэфэя, г. Хэфэй, Китай k.liu@hfut.edu.cn
Лю Кан (Liu Kang)Колледж гражданского строительства при Технологическом университете Хэфэя, г. Хэфэй, Китай k.liu@hfut.edu.cn Ван Юн (Wang Yong)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов, г. Ухань, Китай yongwang93@163.com
Ван Юн (Wang Yong)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов, г. Ухань, Китай yongwang93@163.com  Цзян Цюань (Jiang Quan)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов (г. Ухань) и Университет Китайской академии наук (г. Пекин), Китай qjiang@whrsm.ac.cn
Цзян Цюань (Jiang Quan)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов (г. Ухань) и Университет Китайской академии наук (г. Пекин), Китай qjiang@whrsm.ac.cn  Бершов Алексей Викторовичгенеральный директор ГК «ПЕТРОМОДЕЛИНГ», преподаватель кафедры инженерной геологии Геологического факультета МГУ имени М.В. Ломоносоваalexey.bershov@petromodeling.com
Бершов Алексей Викторовичгенеральный директор ГК «ПЕТРОМОДЕЛИНГ», преподаватель кафедры инженерной геологии Геологического факультета МГУ имени М.В. Ломоносоваalexey.bershov@petromodeling.comПо инициативе и при поддержке ООО «Петромоделинг» редакция журнала «ГеоИнфо» продолжает знакомить читателей с прессиометрическими испытаниями грунтов. Данная группа методов большинством изыскателей и проектировщиков воспринимается просто как «более дешевая и простая альтернатива штамповых испытаний». На деле же это уникальные методы испытаний грунтов в массивах. Они используются для определения как действующих горизонтальных напряжений и коэффициента горизонтального давления грунта в состоянии покоя К0 (без которого, как известно, невозможны оценка начального (природного) состояния геологической среды и дальнейшие расчетные обоснования конструкций), так и физико-механических откликов геологической среды на горизонтальные механические воздействия, например зависимостей между напряжениями и деформациями, а также прочности на сдвиг в недренированных условиях.
Понимание методов оценки напряженно-деформированного состояния грунтового массива очень важно для эффективного перехода к трехмерному моделированию геологической среды и построению ее инженерных цифровых моделей – базовой части информационной цифровой модели объекта капитального строительства, без которой любые информационные проектные построения просто «повисают в воздухе».
Предлагаем вниманию читателей четвертую (заключительную) часть немного сокращенного адаптированного перевода статьи «Исследования озерных глин с использованием самозабуривающегося прессиометра на озере Тайху (Китай)» (ссылка на первоисточник имеется в конце). В этой части рассмотрены: статистический анализ полученных значений секущего модуля сдвига и недренированной сдвиговой прочности, интервалы корреляции флуктуаций этих параметров, а также сделаны общие выводы по всей переведенной работе. Отметим, что нумерация рисунков, формул и таблиц, соответствующая оригиналу, продолжает начатую в предыдущих частях.
Техническая правка выполнена генеральным директором ГК «Петромоделинг» Алексеем Бершовым.
РЕЗУЛЬТАТЫ ИСПЫТАНИЙ САМОЗАБУРИВАЮЩИМСЯ ПРЕССИОМЕТРОМ (продолжение)
Статистический анализ значений секущего модуля сдвига и прочности на сдвиг в недренированных условиях
На основе проанализированных выше результатов можно выполнить статистический анализ величин модуля сдвига и недренированной сдвиговой прочности. В таблице 2 приведены среднее значение, стандартное отклонение и коэффициент вариации COV для модуля сдвига при различных величинах сдвиговых деформаций и для недренированной прочности на сдвиг. Коэффициент вариации COV отражает степень изменчивости свойств грунта на площадке испытаний. Чем выше COV, тем больше изменчивость грунта. Из таблицы 2 видно, что коэффициент вариации значений модуля сдвига составляет около 30% (обычно для диапазона деформаций 0,1–0,5%, как сообщается в литературе [32, 33]).
Таблица 2. Статистические параметры секущего модуля сдвига и недренированной сдвиговой прочности
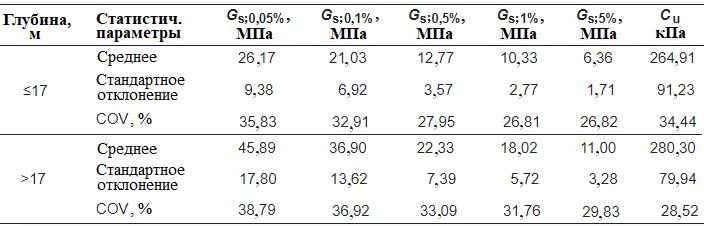
Было интересно обнаружить, что статистические параметры свойств грунтов сильно меняются с определенной глубины. Как видно из таблицы 2, изменения прессиометрических данных в трех скважинах имеют схожие характеристики. Однако, когда глубина превышает 17 м, коэффициент вариации модуля сдвига значительно увеличивается.
Статистический анализ в сочетании с результатами анализа уменьшения модуля показал, что неоднородность грунта увеличивается сверху вниз, особенно при глубине более 17 м. Это может быть связано с историей накопления отложений в районе Тайху, так как в процессе седиментации озерной глины оседают многие биологические остатки и обломочные частицы, в результате чего в грунтах на разной глубине образуются разные прослои. Это может быть основной причиной высокой изменчивости прессиометрических характеристик в вертикальном направлении, что действительно отражает типичные свойства озерных глин, в которых с увеличением глубины чередуется больше подкатегорий каждого типа грунта.
В то же время из таблицы 2 также видно, что сдвиговая деформация весьма отчетливо влияет на распределение коэффициентов вариации, то есть с увеличением деформации COV уменьшается. Это также подтверждают стабильно получаемые результаты, о которых сообщалось ранее, когда модуль сдвига зависит от деформации, а по мере увеличения деформации из-за влияния таких факторов, как пластичность и др., несоответствия откликов разных типов грунтов на нагрузку уменьшаются. Таким образом, при выборе подходящего модуля сдвига при проектировании или численном анализе может оказаться целесообразным тщательное рассмотрение деформированного состояния грунта при приложении нагрузки.
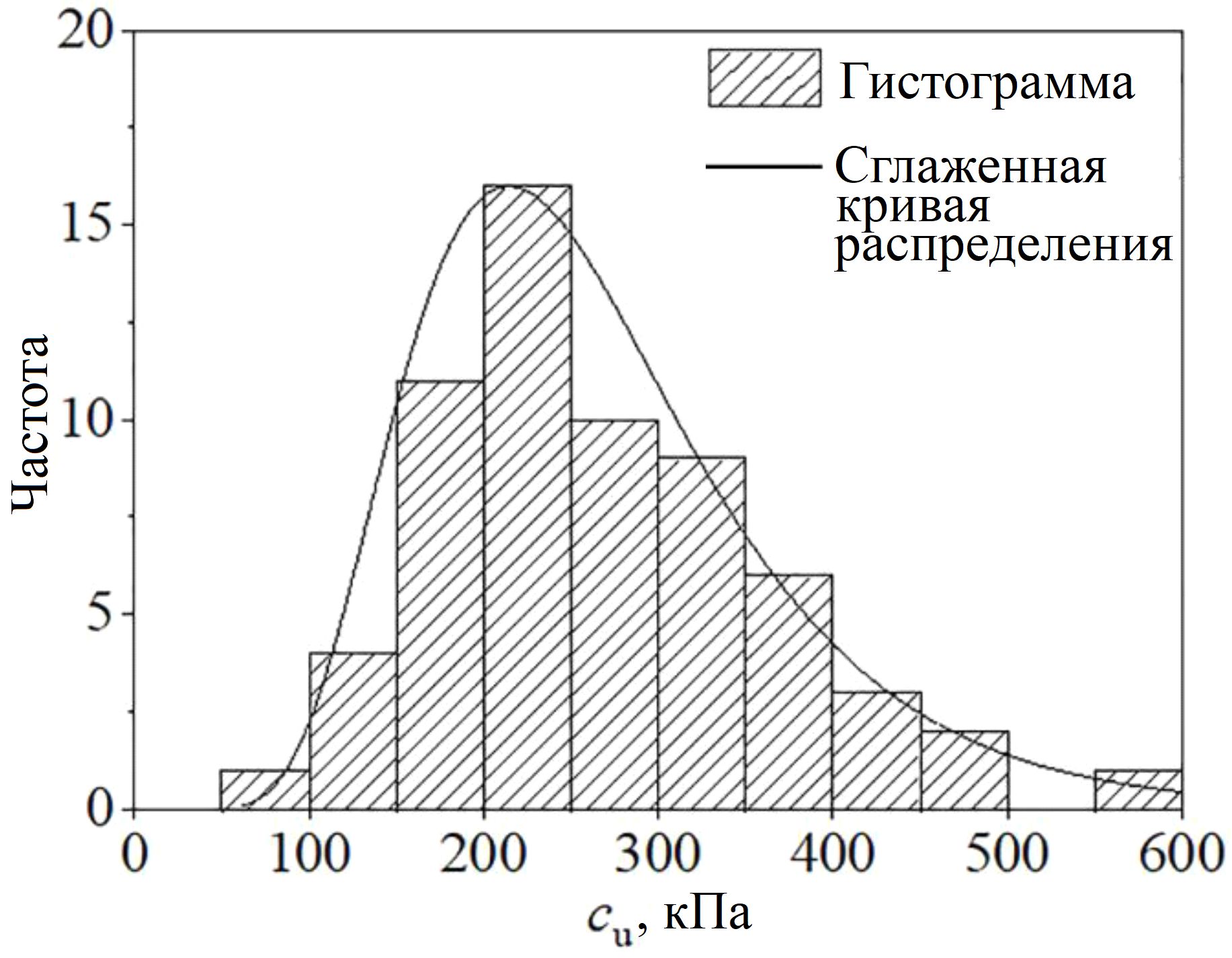
Кроме того, по данным испытаний можно оценить распределение значений недренированной сдвиговой прочности и модуля сдвига. Рисунок 15 показывает, что прочность на сдвиг в недренированных условиях также соответствует логнормальному распределению. Оценка распределений согласуется с данными, приведенными в ранее опубликованных статьях [34, 35]. Например, Гриффитс и др. [34, 35] при анализе устойчивости склонов и откосов рассматривали недренированную сдвиговую прочность как распределенную логнормально. Цзян и Хуан [36] разработали модель нестационарного случайного поля, а прочность глины на сдвиг в недренированных условиях также моделировали как распределенную логнормально.
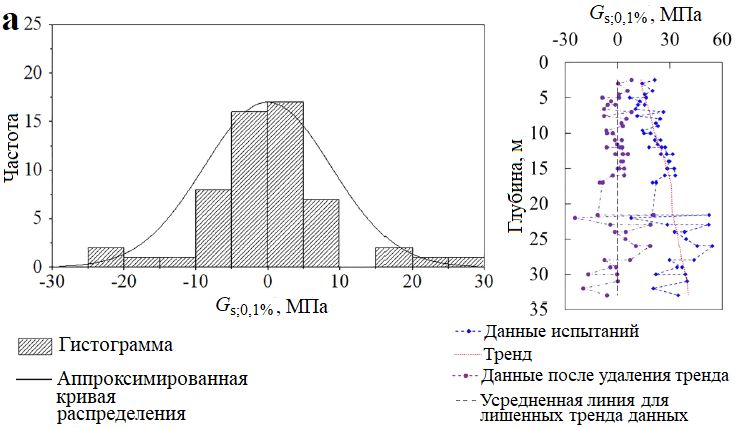
При моделировании случайного поля пространственной изменчивости грунта часто разлагают изменения геотехнических свойств на функцию тренда (например, линейную функцию, как в данном исследовании) и остаток (отражающий так называемую собственную пространственную изменчивость). Затем для моделирования остатка применяются стационарные случайные поля. Другими словами, для обеспечения применимости стационарных случайных полей необходим процесс исключения (удаления) тренда. В связи с этим, поскольку существует тенденция к росту модуля сдвига с увеличением глубины, оценка типа распределения должна выполняться при устранении линейной тенденции. Удаление тренда выполняется с помощью пакета программ MATLAB.
На рисунке 16 справа представлены сопоставления между исходными и измененными исключением тренда секущими модулями сдвига Gs по данным испытаний во всех трех скважинах, а слева показаны гистограммы и сглаженные кривые распределений для лишенных тренда модулей сдвига. По гистограммам можно оценить, что значения Gs после исключения тренда следуют нормальным распределениям. Когда сдвиговая деформация составляет 0,1%, доминирующий диапазон распределений измененных удалением тренда величин Gs находится между минус 10 и 10 МПа. А когда деформация сдвига увеличивается до 5%, лишенные тренда значения Gs в основном находятся в диапазоне от минус 2,5 до 2,5 МПа. Этот результат также согласуется с тем, о чем сообщалось ранее. То есть по мере увеличения сдвиговой деформации модуль сдвига уменьшается (от среднего значения 25 МПа при деформации 0,1% до примерно 8 МПа при деформации 5% для исходных данных). Сходным образом можно также оценить и распределение избавленных от тренда значений модуля сдвига для цикла «разгрузка – повторное нагружение» (Gur), как показано на рисунке 16, г. Величины Gur также соответствуют нормальному распределению, а доминирующий диапазон их распределений находится между минус 10 и 10 МПа.
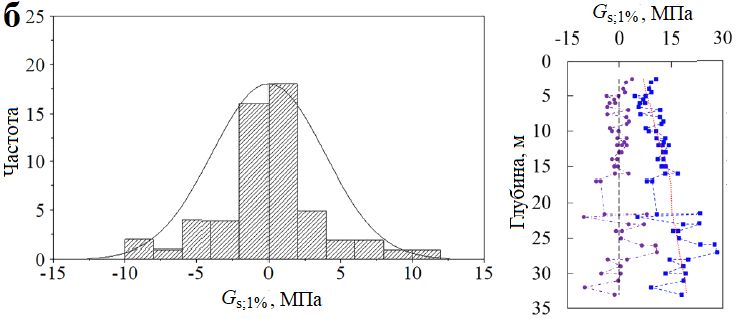
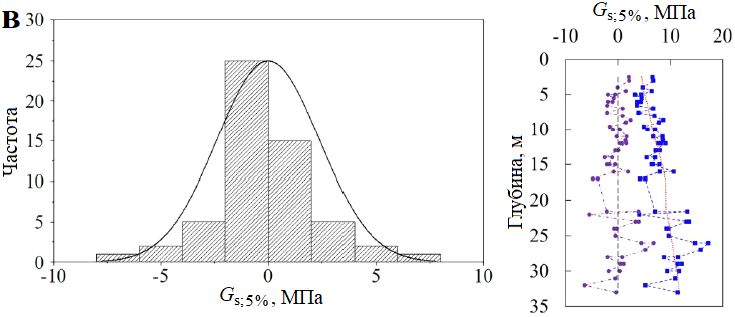
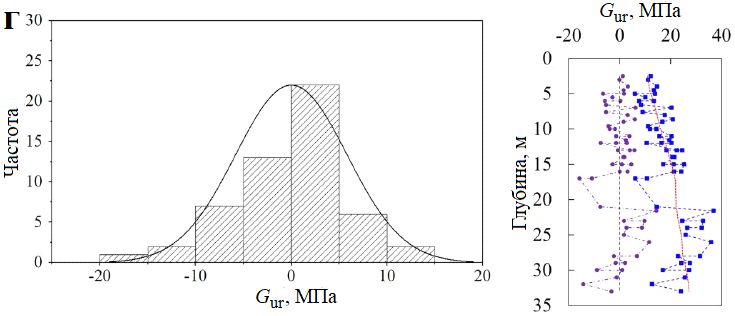
Интервалы корреляции флуктуаций для секущего модуля сдвига и недренированной сдвиговой прочности
В дополнение к средним значениям и стандартным отклонениям параметров грунта пространственная корреляция (в данной статье – интервал корреляции флуктуаций – scale of fluctuation, correllation length) была признана важным параметром, который может повлиять на статистические (вероятностные) результаты. Интервал корреляции флуктуаций можно оценить по результатам испытаний in situ на основе следующего уравнения [37]:

Для моделирования корреляции параметров грунта в разных местах здесь используется обычно применяемая экспоненциальная функция корреляции [38]:

где θ – оцениваемый интервал корреляции флуктуаций.
Интервал корреляции флуктуаций θ рассчитывается на основе минимизации ошибки E:

Значение θ, которое минимизирует ошибку E, можно вычислить, найдя корень следующего выражения:

что может быть выражено так:

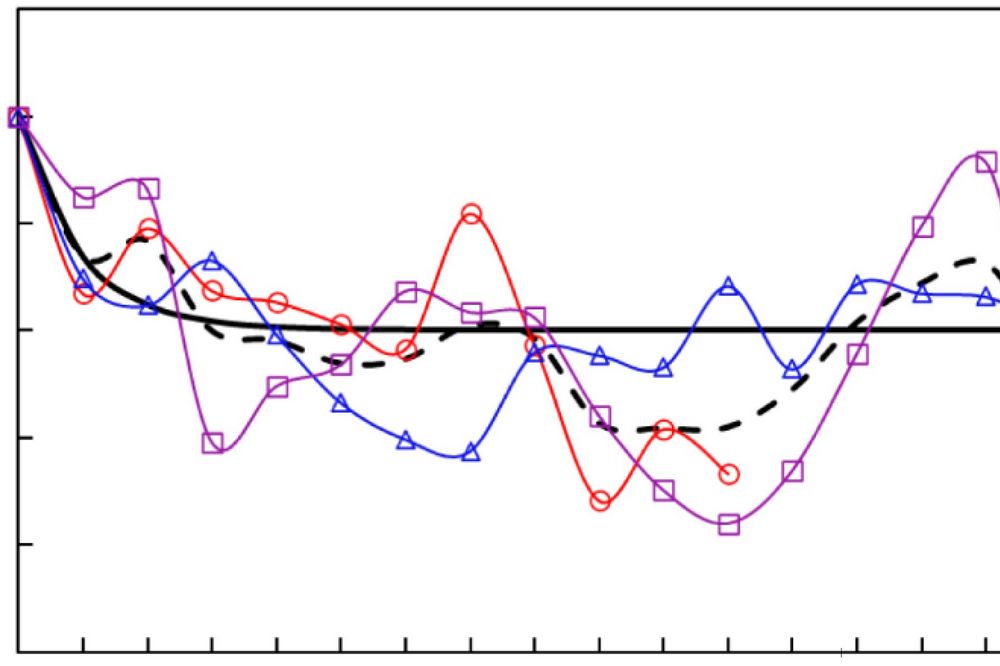
В представленном в данной статье исследовании вертикальные интервалы корреляции флуктуаций (θv) модуля сдвига и недренированной сдвиговой прочности оценивались на основе результатов испытаний самозабуривающимся прессиометром. На рисунке 17 в графическом виде представлены теоретическая и эмпирические корреляционные функции для недренированной прочности на сдвиг cu. Они являются функциями относительного расстояния между двумя разными глубинами, которое в корреляционной функции обычно определяется как вертикальный интервал сбора данных (vertical lag) [38]. Сплошная черная линия обозначает теоретическую корреляцию, оцененную с использованием уравнения (7), а пунктирная черная линия соответствует среднему по трем скважинам. Самый подходящий (best-fit) вертикальный интервал корреляции флуктуаций θv определяется с помощью формулы (10). Средняя оценка θv для недренированной прочности на сдвиг на основе данных, представленных на рисунке 17, составила 1,89 м.
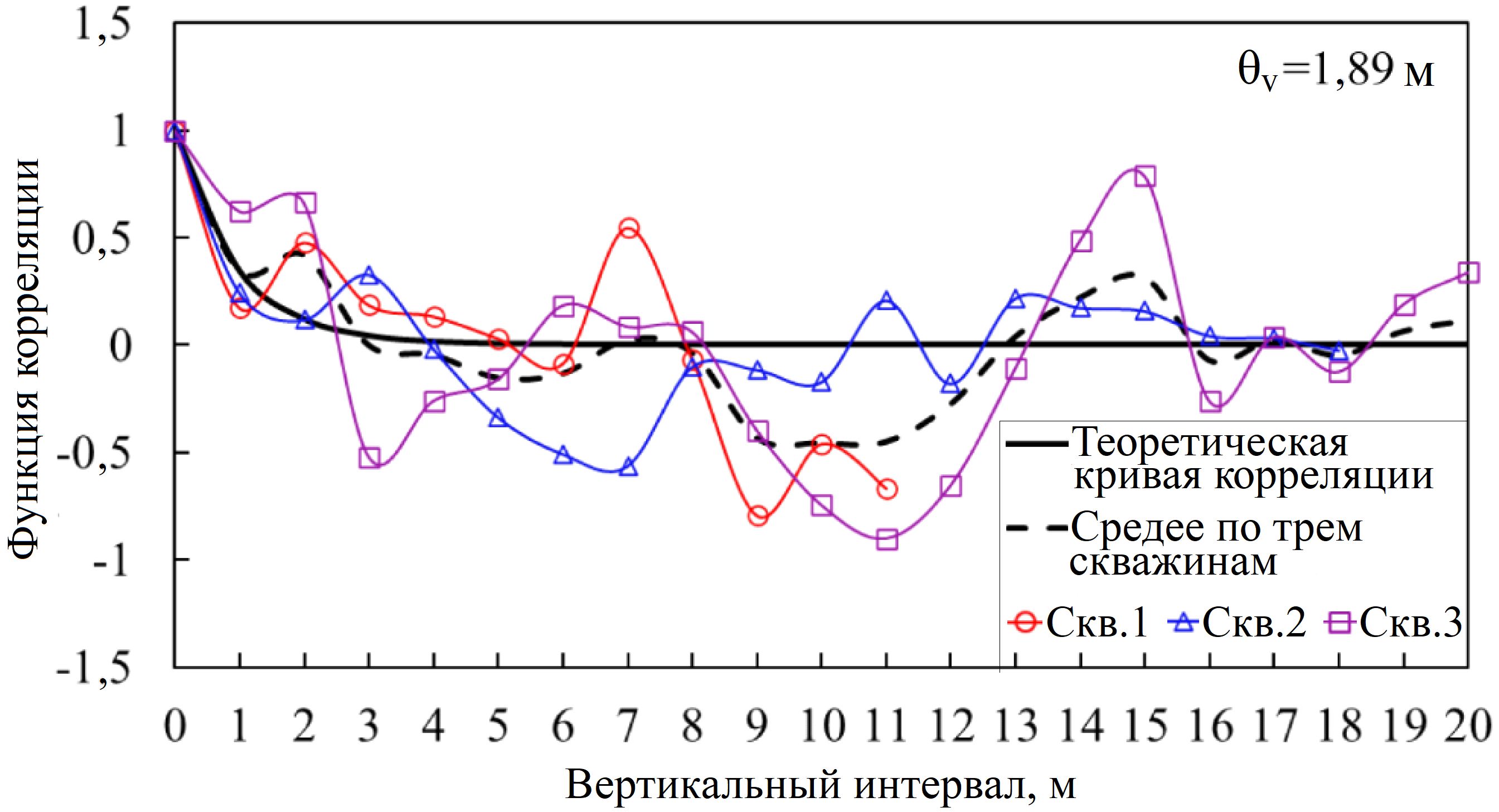
Рис. 17. Теоретическая и эмпирические корреляционные функции для недренированной прочности на сдвиг cu на основе испытаний самозабуривающимся прессиометром в скважинах 1, 2 и 3. Оцененный вертикальный интервал корреляции θv для cu составил 1,89 м
На рисунке 18 показаны аналогичным образом полученные вертикальные интервалы корреляции флуктуаций θv модулей сдвига Gs при различных сдвиговых деформациях в недренированных условиях. Видно, что средняя оценка θv для Gs,0,1% составила 0,74 м; для Gs,1% и Gs,5% они оказались равными 1,53 и 1,62 м соответственно. Это более четко говорит о том, что при изменении деформации от малой (например, 0,1%) до большой (например, 1; 5%) поведение грунта сильно изменяется, при этом вертикальный интервал корреляции флуктуаций θv увеличивается более чем в два раза. При этом, когда деформация растет от 1 до 5%, величина θv практически не меняется. Это также может указывать на то, что, когда деформация увеличивается более чем на 1%, достигается стабильное состояние грунта (как уже отмечалось ранее), но при косвенном суммировании вертикальных корреляционных интервалов для модулей сдвига при различных сдвиговых деформациях. При этом следует отметить, что пространственная корреляция в вертикальном направлении для модуля сдвига при малых деформациях должна быть значительно меньше, чем для недренированной сдвиговой прочности, о чем говорит сравнение значений θv.
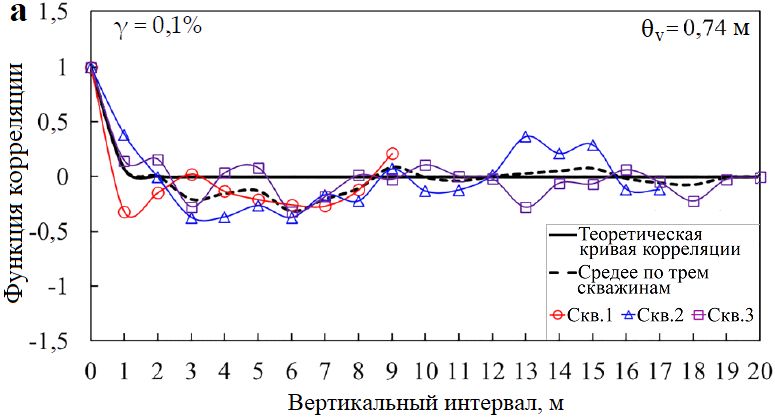
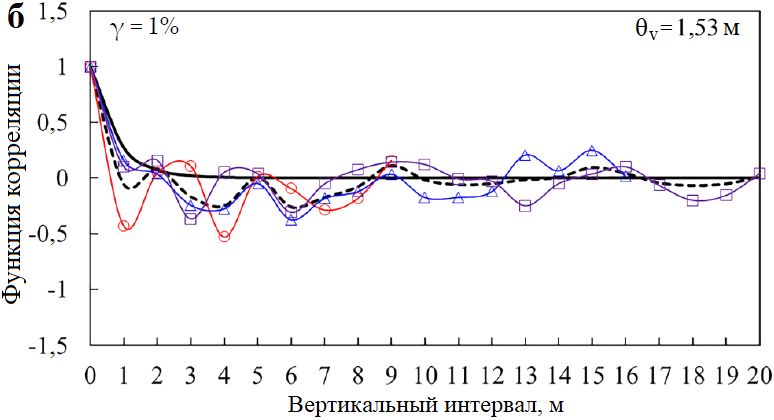
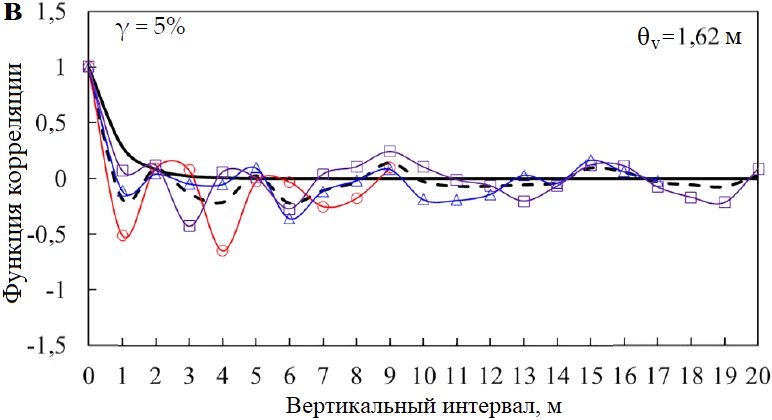
Рис. 18. Теоретические и эмпирические корреляционные функции для секущего модуля сдвига Gs при недренированных сдвиговых деформациях 0,1% (а); 1% (б) и 5% (в) на основе испытаний самозабуривающимся прессиометром в скважинах 1, 2 и 3. Оцененные вертикальные интервалы корреляции θv для Gs составили соответвтвенно 0,74 м (а); 1,53 м (б) и 1,62 м (в)
ВЫВОДЫ
В этой статье представлена всесторонняя интерпретация результатов испытаний самозабуривающимся прессиометром (SBPM) в озерных глинистых отложениях озера Тайху (Китай). Анализировались такие параметры, как начальное (природное) горизонтальное напряжение грунта, прочность на сдвиг в недренированных условиях и модуль сдвига. Сравнение величин недренированной сдвиговой прочности, полученных с помощью прессиометрических испытаний, с полученными в лаборатории, а также рассмотрение аналитических решений по распределению начального давления поровой воды подтвердили достаточную точность результатов испытаний SBPM.
Что касается модуля сдвига, то в целом наблюдалась тенденция к его увеличению с глубиной, что в основном связано с давлением вышележащей толщи грунта. Однако было выявлено, что деформация оказывает большое влияние на значение модуля, что может замедлить скорость его увеличения (то есть по мере роста деформации тенденция к увеличению модуля постепенно уменьшается). Показано, что, когда деформация под нагрузкой растет, модуль сдвига быстро снижается. Но когда деформация превысит 1%, модуль станет постоянным. Модули сдвига для циклов «разгрузка – повторное нагружение» в основном находятся в диапазоне деформаций 1–3,2% и поэтому могут считаться небезопасными, особенно при проектировании фундаментов, где изменения деформаций обычно очень малы.
В статье приведены зависимости между секущим модулем сдвига и числом пластичности. Установлено, что чем больше число пластичности, тем выше модуль сдвига, а вместе с тем и скорость его уменьшения. Статистический анализ прессиометрических параметров показал, что недренированная сдвиговая прочность подчиняется логнормальному распределению, а модуль сдвига – нормальному. Кроме того, суммируя интервалы корреляции флуктуаций для секущего модуля сдвига при различных сдвиговых деформациях, также можно наблюдать отчетливое влияние деформации на изменения модуля, а пространственная корреляция по вертикали для модуля сдвига при малых деформациях должна быть намного меньше, чем для недренированной прочности на сдвиг.
ИСТОЧНИК ДЛЯ АДАПТИРОВАННОГО ПЕРЕВОДА
Wang B., Liu K., Wang Y., Jiang Q. Site investigations of the lacustrine clay in Taihu Lake, China, using self-boring pressuremeter test // Sensors (Special Issue “Fault Detection and Data Analysis for Structure and Infrastructure Engineering”). 2021. Vol. 21 (6026). DOI: doi.org/10.3390/s21186026. URL: mdpi.com/1424-8220/21/18/6026.
СПИСОК ЛИТЕРАТУРЫ, ИСПОЛЬЗОВАННОЙ АВТОРАМИ ПЕРЕВЕДЕННОЙ СТАТЬИ
- Benoit J., Clough G.W. Self-boring pressuremeter tests in soft clay // J. Geotech. Eng. 1986. Vol. 112. P. 60–78.
- Fahey M., Carter J.P. A finite element study of the pressuremeter test in sand using a nonlinear elastic plastic model // Can. Geotech. J. 1993. Vol. 30. P. 348–362.
- Baquelin F., Jezequel J.F., Shields D.H. The pressuremeter and foundation engineering. Clausthal-Zellerfeld, Germany: Trans Tech Publications, 1978.
- Lv J., Zhou T., Du Q., Wu H. Experimental investigation on properties of gypsum-quicklime-soil grout material in the reparation of earthen site cracks // Constr. Build. Mater. 2017. Vol. 15. P. 253–262.
- Worth C.P., Hughes J.M.O. An instrument for the in-situ measurement of the properties of soft clays // Proc. 8th Int. Conf. Soil Mech. Found. Eng. 1973. Vol. 12. P. 487–494.
- Clarke B.G. In situ testing of clay using Cambridge self-boring pressuremeter: Ph.D. thesis. Cambridge, UK: Cambridge University, 1981.
- Mair R.J., Wood D.M. Pressuremeter testing: methods and interpretation. London, UK; New York, NY, USA: Butterworths, Construction Industry Research and Information Association, 1987.
- Palmer A.C. Undrained plane strain expansion of a cylindrical cavity in clay: a simple interpretation of the pressuremeter test // Geotechnique. 1972. Vol. 22. P. 451–457.
- Ladanyi B. In-situ determination of undrained stress-strain behaviour of sensitive clays with the pressuremeter // Can. Geotech. J. 1972. Vol. 9. P 313–319.
- Baguelin F., Jezequel J.-F., Lemee E., Le Mehaute A. Expansion of cylindrical probes in cohesive soils // J. Soil Mech. Found. Div. ASCE, 1972. Vol. 98. P. 1129–1142.
- Houlsby G.T., Withers N.J. Analysis of the cone pressuremeter test in clay // Geotechnique. 1988. Vol. 38. P. 575–587.
- Jefferies M.G. Determination of horizontal geostatic stress in clay with the self-bored pressuremeter // Can. Geotech. J. 1988. Vol. 25. P. 559–573.
- Bellotti R., Ghionna V., Jamiolkowski M., Robertson P.K., Peterson R.W. Interpretation of moduli from self-boring pressuremeter tests in sand // Geotechnique. 1989. Vol. 39. P. 269–292.
- Ferreira R.S., Robertson P.K. Interpretation of undrained self-boring test results incorporating unloading // Can. Geotech. J. 1992. Vol. 29. P. 918–928.
- Ferreira R.S., Robertson P.K. Large-strain undrained pressuremeter interpretation based on loading and unloading data // Can. Geotech. J. 1994. Vol. 31. P. 71–78.
- Schnaid F., Ortigao J.A., Mantaras F.M., Cunha R.P., Macgregor I. Analysis of self-boring pressuremeter (SBPM) and Marchetti dilatometer (DMT) tests in granite saprolites // Can. Geotech. J. 2000. Vol. 37. P. 796–810.
- Silvestri V. Assessment of self-boring pressuremeter tests in sensitive clay // Can. Geotech. J. 2003. Vol. 40. P. 362–387.
- Kayabasi A. Prediction of pressuremeter modulus and limit pressure of clayey soils by simple and non-linear multiple regression techniques: a case study from Mersin, Turkey // Environ. Earth Sci. 2012. Vol. 66. P. 2171–2183.
- Whittle R.W., Liu L. A method for describing the stress and strain dependency of stiffness in sand // Proceedings of the 18th International Conference on Soil Mechanics and Geotechnical Engineering, Paris, France, 2–6 September 2013.
- Mehdi A.M., Ehsan K. Interpretation of in situ horizontal stress from self-boring pressuremeter tests in sands via cavity pressure less than limit pressure: a numerical study // Environ. Earth Sci. 2017. Vol. 76. P. 333.
- Christian J.T., Baecher G.B. Probabilistic foundation settlement on spatially random soil // J. Geotech. Geoenviron. 2003. Vol. 129. P. 866.
- Santoso A.M., Phoon K.K., Quek S.T. Effects of soil spatial variability on rainfall-induced landslides // Comput. Struct. 2011. Vol. 89. P. 893–900.
- Li Y., Hicks M.A., Nuttall J.D. Comparative analyses of slope reliability in 3D // Eng. Geol. 2015. Vol. 196. P. 12–23.
- Firouzianbandpey S., Griffiths D.V., Ibsen L.B., Andersen L.V. Spatial correlation length of normalized cone data in sand: case study in the north of Denmark // Can. Geotech. J. 2014. Vol. 51. P. 844–857.
- De Gast T., Vardon P.J., Hicks M.A. Estimating spatial correlations under man-made structures on soft soils // Geo-Risk. 2017. P. 382–389.
- Bolton M.D., Whittle R.W. A non-linear elastic / perfectly plastic analysis for plane strain undrained expansion tests // Geotechnique. 1999, Vol. 49. P. 133–141.
- Gibson R.E., Anderson W.F. In situ measurement of soil properties with the pressuremeter // Civ. Eng. Public Work. Rev. 1961. Vol. 56. P. 615–618.
- Ching J., Phoon K.K. Multivariate distribution for undrained shear strengths under various test procedures // Can. Geotech. J. 2013. Vol. 50. P. 907–923.
- Li L., Wang Y., Cao Z. Probabilistic slope stability analysis by risk aggregation // Eng. Geol. 2014. Vol. 176. P. 57–65.
- Li D.Q., Zheng D., Cao Z.J., Tang X.S., Phoon K.-K. Response surface methods for slope reliability analysis: review and comparison // Eng. Geol. 2016. Vol. 203. P. 3–14.
- Liu L.-L., Deng Z.-P., Zhang S.-H., Cheng Y.-M. Simplified framework for system reliability analysis of slopes in spatially variable soils // Eng. Geol. 2018. Vol. 239. P. 330–343.
- Kulhawy F.H., Roth M.J.S., Grigoriu M.D. Some statistical evaluations of geotechnical properties // Proceedings of the 6th International Conference on Applied Statistics Probability in Civil Engineering (ICASP6), Mexico City, Mexico, 17–21 June 1991.
- Griffiths D.V., Fenton G.A. Probabilistic slope stability analysis by finite elements // J. Geotech. Geoenvironmental. Eng. 2004. Vol. 130. P. 507–518.
- Griffiths D.V., Huang J., Fenton G.A. Influence of spatial variability on slope reliability using 2-d random fields // J. Geotech. Geoenviron. 2009. Vol. 135. P. 1367–1378.
- Griffiths D.V., Yu X. Another look at the stability of slopes with linearly increasing undrained strength // Geotechnique. 2015. Vol. 65. P. 824–830.
- Shui-Hua J., Jinsong H. Modeling of non-stationary random field of undrained shear strength of soil for slope reliability analysis // Soils Found. 2018. Vol. 58. P. 185–198.
- Jaksa M.B. The influence of spatial variability on the geotechnical design properties of a stiff over-consolidated clay: Ph.D. thesis. Adelaide, Australia: University of Adelaide, 1995.
- Vanmarcke E.H. Probabilistic modeling of soil profiles // ASCE J. Geotech. Eng. 1977. Vol. 103. P. 1227–1246.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц