Модель Хука – Брауна с разупрочнением сделает геотехнические решения более надежными

Введение

 

На текущий момент большинство геомеханических прогнозов, использующих численные конечноэлементные методы, базируется на применении упругопластических моделей, работающих исключительно с допредельной стадией деформирования. При достижении предельного состояния такими моделями описывается либо последующее идеально-пластическое течение, либо идеально-пластическое течение с упрочнением за счет дилатансии. Исключение составляют программные комплексы, способные учитывать идеально-хрупкое разрушение и остаточную прочность, но не рассматривающие процесс разупрочнения.

Включение описания поведения скальных грунтов на запредельной стадии деформирования позволит уточнить размер и форму зон предельного состояния и, кроме того, разбить эту стадию на две части в соответствии с протекающими на ней процессами. В первой из них еще идет процесс разупрочнения, то есть происходит развитие пластических деформаций при незначительных изменениях напряженного состояния. Во второй части скальные породы уже перешли к остаточной прочности.

При этом разупрочнение (плавное снижения прочности до остаточной) может не проявляться при испытаниях образцов ненарушенной структуры, а возникать только в массивах скальных грунтов со средней или значительной трещиноватостью (что характерно для большинства массивов скальных пород), а это очень важно учитывать при геотехническом проектировании.

Одна из возможностей описания процесса разупрочнения скального грунта при переходе к остаточной прочности появилась в 2019 году за счет использования модели Хука – Брауна с разупрочнением (Hoek & Brown model with softening – HBS), разработанной за счет усовершенствования известной модели Хука – Брауна (Hoek & Brown model – HB).

 

Модель Хука – Брауна

 Наибольшее распространение для описания массивов трещиноватых скальных грунтов получила модель Хука – Брауна (Hoek-Brown model – HB). (В публикациях на русском языке практически с одинаковой частотой встречаются разные написания фамилии Hoek – Хук, Хёк, Хоук, Хоек, Хок. – Ред.).

Это изотропная линейно-упругая идеально-пластическая модель с критерием прочности Хука – Брауна [1, 10]. Она включена в большинство программных комплексов для геотехнических расчетов на основе метода конечных элементов (МКЭ).

Критерий Хука – Брауна является развитием критерия прочности Мора – Кулона. Усовершенствование заключается в нелинейной форме зависимости «τ – σ», которая для критерия Мора – Кулона является линейной. Широко известно, что нелинейная форма в большей степени соответствует результатам лабораторных испытаний скального грунта, а также заложена в основу построения паспорта прочности скальной породы.

Для определения момента возникновения пластических деформаций используется критерий Хука – Брауна 2002 года [10]:

 

 

где σ₁, σ₃ – соответственно наибольшее и наименьшее главное напряжение; σ_ci – предельная прочность ненарушенной породы при отсутствии бокового давления (в наиболее актуальной работе [9] Хук отличает предел прочности на одноосное сжатие UCS от σ_ci); m_b, α, s – безразмерные параметры, которые не имеют физического смысла, но влияют на форму и степень нелинейности предельной огибающей Хука.

Параметры m_b, α, s зависят от геологического индекса прочности GSI и от  коэффициента нарушенности D [17] в соответствии со следующими уравнениями:

 

 

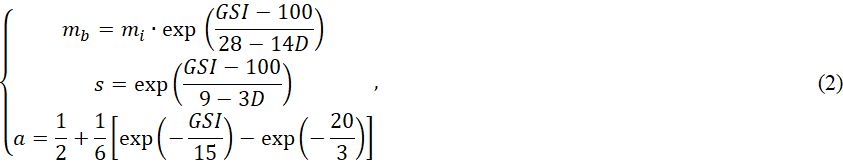
где m_i – параметр ненарушенной породы, который  в значительной степени влияет на степень нелинейности предельной огибающей Хука в плоскости «σ₁ – σ₃» и который снижается до величины m_b в зависимости от степени нарушенности массива (при GSI = 100m_b = m_i).

По величине σ_ci можно определить предел прочности на одноосное сжатие и на двухосное растяжение. При σ₃ = 0 уравнение (1) приобретает вид:

 

 

 При использовании в большинстве программных продуктов в уравнениях (3) меняется знак.

На рисунке 1 представлена поверхность текучести Хука – Брауна в пространстве главных напряжений и на девиаторной плоскости. Эта поверхность не гладкая, поэтому при использовании ассоциированного закона пластического течения возникает известная проблема расчета пластических деформаций в ее углах. В руководстве к программному комплексу Plaxis [2] частично описывается подход к решению этой проблемы углов. Он аналогичен используемому для поверхности текучести Мора – Кулона и заключается в том, что вместо одной функции текучести и пластического потенциала используется шесть (в соответствии с количеством плоскостей, формирующих поверхность текучести).

 

 

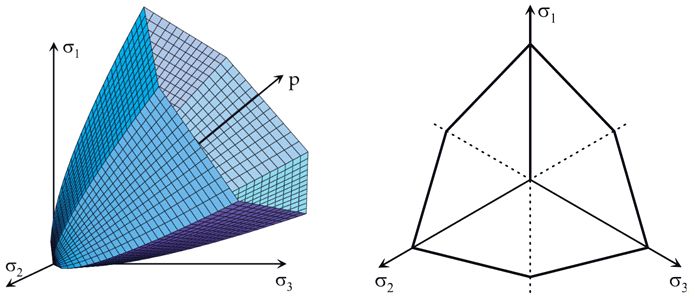
 Наиболее существенным отличием при использовании модели в программных комплексах является учет упрочнения, которое реализуется до предельной прочности, и разупрочнения, которое происходит после разрушения и стремится к остаточной прочности. В Plaxis для учета упрочнения/разупрочнения необходимо использовать пользовательскую модель, которая появилась в этой программе лишь в последние годы.

Важной частью любой механической модели является то, каким образом она описывает пластическое деформирование. На рисунке 2 представлены три основных варианта поведения материала при пластическом деформировании. В первом из них (см. рис. 2, а) материал достигает предела упругости, после чего его прочность повышается до предельной без ярко выраженного пика. Второй вариант (см. рис. 2, б) представляет собой идеализацию реального поведения. Что касается третьего случая, то, как отмечали Вермеер и Де Борст [21], феномен пиковой прочности, который на графике отражает характерная точка перегиба (см. рис. 2, в), связан с дальнейшим быстрым разупрочнением материала при активном формировании линий скольжения, которые усложняют качественное моделирование.

 

 

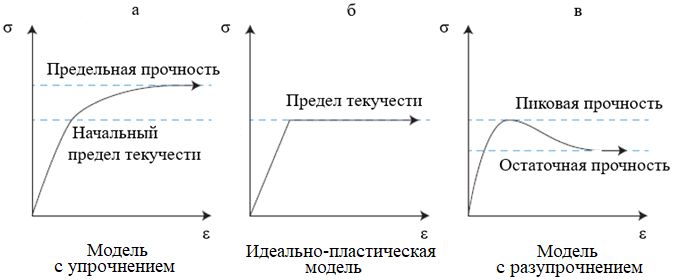
 Обычно разупрочнение описывает процесс разрушения массивов скальных грунтов, который начинается с появления микротрещин, за которым следует их дальнейшее раскрытие, распространение и, наконец, разрушение материала.

Вместе с тем принципиально важно учитывать остаточную прочность и траекторию ее достижения после разрушения. Как отмечал Хук, скальная порода хорошего качества разрушается хрупко, а с ухудшением ее качества, то есть с увеличением ее трещиноватости, ситуация стремится к представленной на рисунке 2, б.

 

Модель Хука – Брауна с разупрочнением

 Ряд программных комплексов позволяет учитывать остаточную прочность и переход к ней при идеально-хрупком разрушении. Но в Plaxis для этой цели необходимо применять пользовательскую модель Хука – Брауна с разупрочнением (Hoek & Brown model with softening – HBS) [15].

В основе модели HBS используется модифицированный критерий прочности, предложенный Цзяном (Jiang) [11]. Этот критерий гарантирует одновременно гладкость и выпуклость поверхности текучести. Кроме того, базовая реализация модели дополнительно улучшена за счет следующих основных функций:

• исходной неассоциированной пластичности с возможностью моделирования нелинейного изменения дилатансии в постпиковом режиме;
• правил учета разупрочнения, которые описываются двумя разными формулами;
• ограничения напряжений в зоне растяжения;
• использования версии модели Хука – Брауна, зависящей от скорости деформирования, что необходимо для численных решений, основанных на первоначальном построении сетки конечных элементов, когда хрупкое разрушение характеризуется значительной концентрацией деформаций в узких полосах сдвига.

 На рисунке 3 в графической форме описан механизм учета разупрочнения (остаточной прочности).

 

 

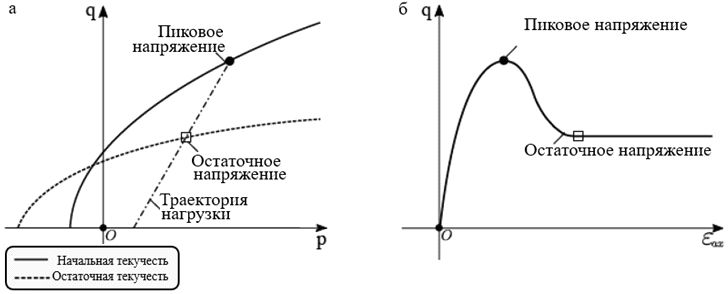
 Для корректировки разбиения сетки конечных элементов и ее объективного учета после преодоления предела прочности используется так называемый метод вязкой регуляризации.

 

Основные формулы

 Для возможности учета влияния среднего главного напряжения на положение поверхности текучести Цзян (Jiang) и Чжао (Zhao) [12] предложили рассмотреть обобщение классической модели Хука – Брауна с точки зрения инвариантов напряжений (среднего напряжения p, девиаторного напряжения q и угла Лоде θ):

 

 

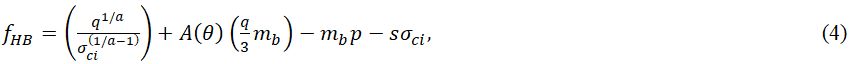
где функция А(θ) принимается в соответствии со статьей [11]:

 

 

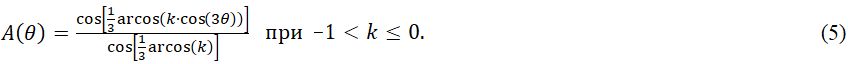
Введенный Цзяном и Чжао [12] параметр k можно рассматривать как дополнительный параметр модели, позволяющий лучше калибровать поведение образца скального грунта при девиаторном нагружении (k = 0 соответствует круглому сечению в девиаторной плоскости; k → –1 соответствует сечению, определенному Цзяном и Чжао [12], рис. 4). Хотя при k → –1 этот параметр может гарантировать более точное приближение к исходной поверхности текучести модели Хука – Брауна (уравнению (1)), такая поверхность будет характеризоваться разрывом ее первой производной (градиента поверхности текучести ∂f/∂σ_ij) вдоль траекторий трехосных сжимающих напряжений. В связи с этим при трехосном напряженном состоянии рекомендуется избегать значения k = –1. Поэтому по умолчанию нижняя граница этого параметра соответствует значению минус 0,9999.

Представление критерия Хука – Брауна на рисунке 4, a (по Цзяну [11]) нанесено на девиаторную плоскость, где сравниваются различные поверхности текучести при изменении параметра k. На основе анализа полученных диаграмм стоит отметить, что для осесимметричных траекторий напряжений трехмерное обобщение, предложенное Цзяном [11], сходится к исходной формуле модели (1). На рисунке 4, б функция А(θ) также построена для нескольких значений параметра k.

 

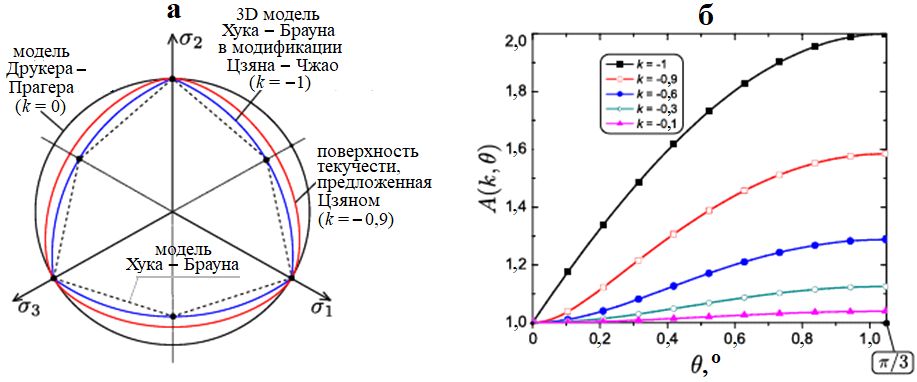
Рис. 4. Cледы поверхностей текучести, предложенные Цзяном, при изменениях параметра k (а) и изменения функции А(k,θ) в зависимости от угла Лоде θ (б)

 

Для расчета пластических деформаций пластический потенциал был определен в форме, схожей с таковой для поверхности текучести. Уравнение для функции пластического потенциала отличается от формулы для поверхности текучести только на основе переменной m_ψ, что позволяет моделировать ассоциированный закон пластического течения в случае m_b = m_ψ:

 

 

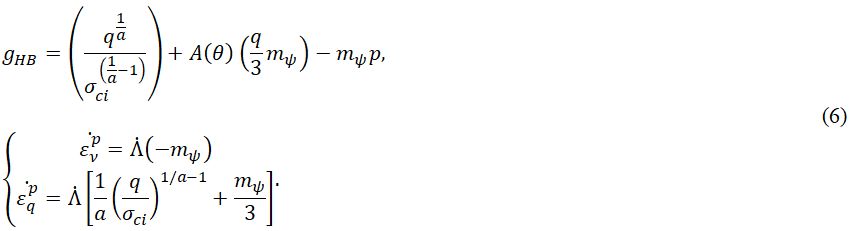
Некоторые входные параметры модели HBS и их диапазоны в зависимости от типа скальных пород и влияющих факторов будут рассмотрены в следующих разделах.

 

Правило разупрочнения

 Деградация материала при сдвиге моделируется с помощью правила разупрочнения, при котором уменьшение переменных упрочнения Г_j задается как функция от эквивалентной пластической деформации ε^p_eq (накопленных значений пластических деформаций формоизменения), что позволяет описать разрушение материала при сдвиге. В частности, гиперболический спад Г_j приближается к его остаточному значению при больших значениях пластической деформации в соответствии с правилом разупрочнения, предложенным Барничоном (Barnichon, 1988) и Коллином (Collin, 2003):

 

 

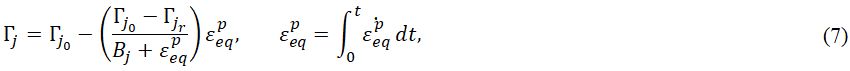
где Г_j0, Г_jr – соответственно начальная и остаточная величина Г_j; B_j – параметр материала, определяющий скорость разупрочнения и соответствующий j-той переменной упрочнения.

На рисунке 5 показаны нормированные изменения Г_j для различных значений параметров B_j, где B_j = ε^p_eq (некоторые значения Г_j, при которых происходит 50%-ная деградация: Г_j = 0,5(Г_j0 + Г_jr)).

 

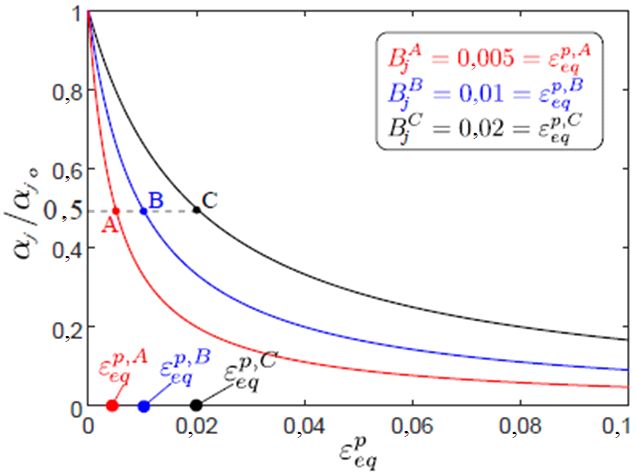
Рис. 5. Развитие нормализованной (приведенной к единичному размеру) переменной разупрочнения Г_j по отношению к ее начальному значению Г_j0. Кроме того, показано влияние параметра B_j на величину разупрочнения

 

В модели HBS величина остаточной прочности зависит от значения бокового давления σ₃ и также описывается критерием Хука – Брауна. В этом случае все параметры, включенные в этот критерий, обретают индекс r или res и служат для описания остаточной прочности. Исключение составляет параметр σ_ci, который имеет одну и ту же величину для уравнений, описывающих предельную прочность, и для формул, описывающих остаточную прочность.

Исследовались и возможности для описания остаточной прочности в зависимости от величины всестороннего обжатия для разных типов скальных пород. При этом не существует какого-либо стандартизированного подхода для определения параметров по кривым остаточной прочности.

В программном комплексе Plaxis опционально можно выбрать один из следующих двух подходов для использования правила разупрочнения, представленного в уравнениях.

1. Определение уменьшения показателей свойств материала m_b и s по предложению Алонсо (Alonso) и др. [6], Цзоу (Zou) и др. [23], которое далее именуется моделью предельного разупрочнения (Strength Softening Model – SSM). При этом подходе уменьшение показателей свойств материала применяется напрямую через переменные m_b и s, как это было сделано в работе Маринелли (Marinelli) и др. [16], что позволяет представить уравнение (7) следующим образом:

 

 

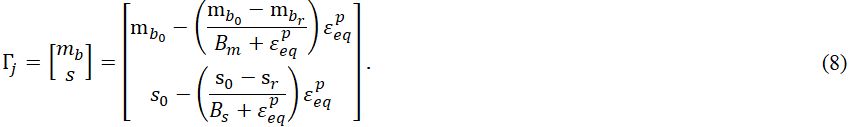
2. Определение уменьшения геологического индекса прочности GSI, как предложили Цай (Cai) и др. [7, 13, 19], которое далее именуется моделью разупрочнения GSI (GSI Softening Model – GSM). Этот подход основан на предположении о том, что уравнения, изначально предложенные Хуком (Hoek) [10] для связывания прочности ненарушенного образца с прочностью массива этого скального грунта in situ, также связывают прочность ненарушенного образца с остаточной прочностью изначально неповрежденной породы.

Цай (Cai) и др. [7] предложили формулу для получения остаточной величины геологического индекса прочности GSI_r на основе исходного значения GSI₀ (равного 100 для ненарушенного массива скальных грунтов). Эту величину можно использовать для оценки остаточной прочности массива с использованием обобщенного метода Хука – Брауна [10].

При этом GSI используется в качестве параметра упрочнения. Таким образом, разупрочнение материала происходит с помощью эмпирических соотношений, представленных в формуле (2). Такая стратегия согласуется с результатами исследования [7] по определению остаточных свойств массива скальных пород, согласно которым процесс разупрочнения связан с комбинацией двух основных факторов:

1) развития микротрещин и других разрывов сплошности и нарушений;

2) гладкости поверхности скольжения, влияющей на прочность образца (рис. 6).

 

Ухудшение качества породы отражается через уменьшение GSI:

 

 

где GSI₀ и GSI_r – соответственно начальная и остаточная величина GSI; B_GSI – параметр материала, определяющий скорость разупрочнения.

Подставив уравнение (9) в формулу (2), можно получить обобщенное выражение правила разупрочнения для рассматриваемого второго подхода GSM:

 

 

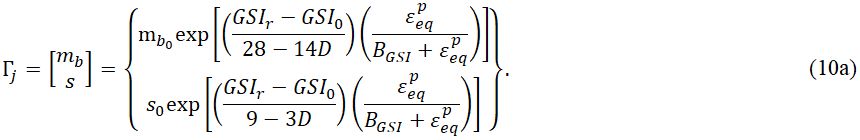
Важно отметить, что для согласования с параметрами, определяющими критерий текучести и систему GSI (см. формулу (1)), показатель степени α (см. формулу (1)) может быть добавлен между переменными упрочнения, указанными в векторе Г, – и таким образом будет установлена зависимость между α и GSI. Для простоты, а также из-за ограниченного диапазона значений α этот коэффициент будет оставаться постоянным и, соответственно, будет определяться по начальному значению GSI:

 

 

На рисунке 6 продемонстрировано развитие GSI в процессе деградации массива скальных грунтов.

 

 

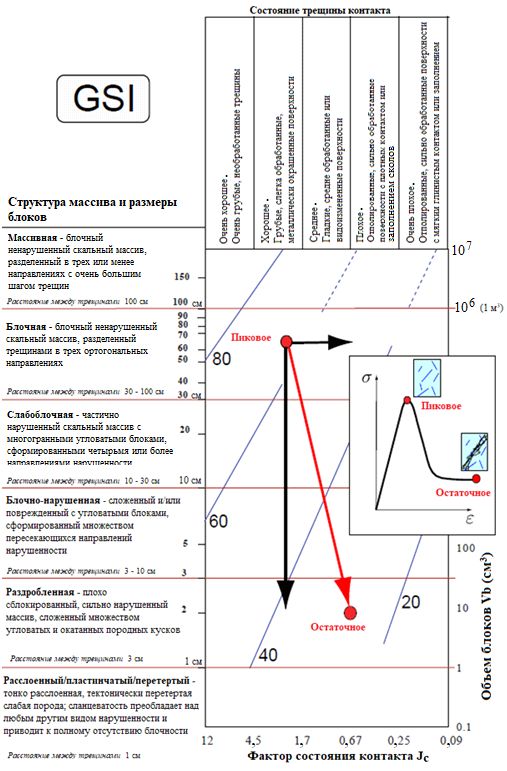
 В последние десятилетия для оценки остаточных значений m_b и s в литературе было предложено несколько эмпирических соотношений. Рибакки (Ribacchi) [20] предложил вычислять m_br и s_r как доли от их начальных значений: m_br = 0,65m_b0; s_r = 0,04s₀. В дальнейшем это предложение было усовершенствовано за счет изменения указанных соотношений в зависимости от GSI. В этом направлении Цай (Cai) и др. [7] и Алехано (Alejano) и др. [5] получили следующие эмпирические соотношения для GSI_r как функции GSI₀:

 

 

Эволюция GSI_r согласно формулам (11) показана на рисунке 7, где качество породы указано в зависимости от начального значения GSI₀. Стоит отметить, что для значений GSI₀ ≤ 25 предлагается ввести ограничение для уравнений (11) (см. рис. 7), что вытекает из недостаточной изменяемости параметров m_b0, s₀ и α (рассчитанных для GSI₀ ≤ 25).

 

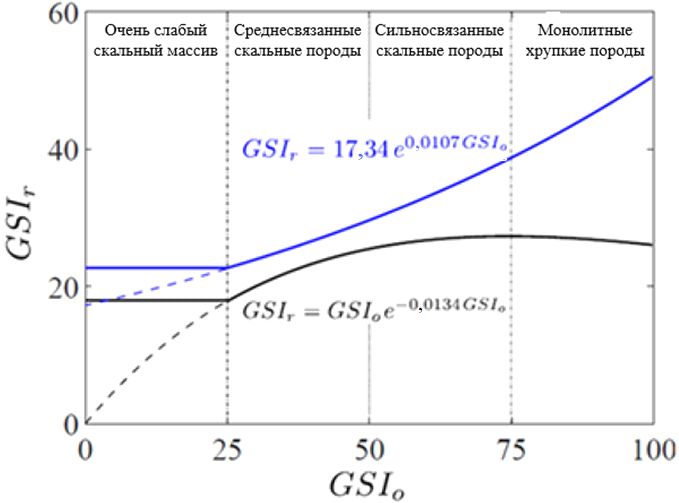
Рис. 7. Развитие GSI_r по формулам (11)

 

Нелинейная дилатансия скальных грунтов

 

Понимание поведения скальных грунтов после достижения поверхности текучести и развития пластических деформаций является критически важной составляющей при решении геомеханических задач. В вопросах строительства горных выработок точное предсказание зоны развития пластических деформаций имеет существенное влияние на параметры крепления и устойчивость обнажений скальных пород.

Модель должна достоверно учитывать развитие объемных деформаций после достижения предела прочности. Для этой цели обычно вводят угол дилатансии ψ, определяемый по следующей формуле [21]:

 

 

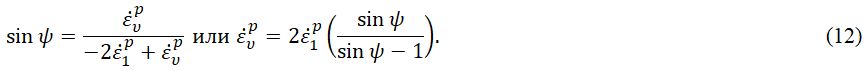
Подставив выражение для пластического потенциала (6) в уравнение (12), можно связать угол дилатансии с параметром модели Хука – Брауна:

 

 

 В условиях трехосного нагружения уравнение (13) эквивалентно классической формуле (1). В таком случае дилатансию можно выразить следующим образом:

 

 

или

 

 

В уравнении (15) нелинейное изменение m_ψ как функции пластической деформации может быть задано при использовании одной из формул, представленных в литературе [4, 22 и др.]. В предложенной модели тенденция поведения угла дилатансии обеспечивается за счет явной изменяемости m_ψ (для формул SSM и GSM), что гарантирует плавный переход от ассоциированной пластичности к неассоциированной, а также уменьшение угла дилантансии по мере перехода к запредельной прочности. Хотя уравнение (15) не рассматривается для моделирования дилатансии, оно будет учтено для определения начального значения этого параметра (m_ψ0).

 

Моделирование дилатансии для моделей типа Хука – Брауна

 

Для рассмотренного выше подхода SSM изменение переменной m_ψ описывается формулой:

 

 

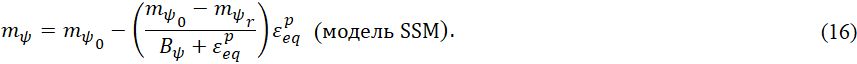
 Уравнение (16) может быть упрощено. При исключении переменной m_ψr (которая приблизительно равна нулю) получим:

 

 

Для рассмотренного выше подхода GSM изменение переменной m_ψ описывается уравнением:

 

 

где F_ψ – параметр, введенный для возможности снижения m_ψ при уменьшении GSI.

Подставив выражение для GSI (9) в уравнение (18), можно описать развитие m_ψ следующим образом:

 

 

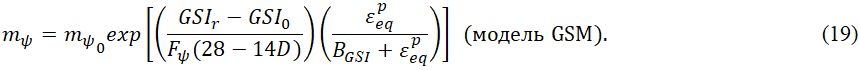
Чтобы разделить влияние параметра на учет качества массива скальных грунтов и на вклад породы ненарушенной структуры, F_ψ можно представить так:

 

 

где GSI₀ⁱ, GSI_rⁱ – начальная и остаточная величина GSI для ненарушенного образца скального грунта (GSI₀ⁱ = 100; GSI_rⁱ ≈ 35); F_ψⁱ – показатель дилатансии скальной породы ненарушенной структуры (поэтому он может быть определен на основе экспериментальных данных путем калибровки).

Значение m_ψ0 можно определить путем калибровки этого параметра на основе результатов лабораторных испытаний (по [14]). В следующем разделе описывается методика, позволяющая качественно оценить m_ψ0, и связываются принятые формулы с эмпирическими соотношениями, предлагаемыми в литературе.

 

Определение параметра m_ψ0

 Чтобы рассмотреть возможный способ введения зависимости GSI от значения начального угла дилатансии, уравнение (15) считается характеризующим дилатансию с начала текучести, то есть используются значения параметров m_b0 и ψ₀. Тогда получается:

 

 

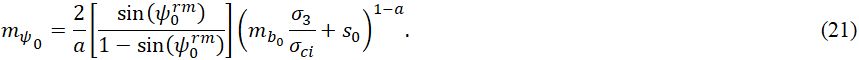
 Формулой (21) будет описываться влияние массива скального грунта не только на параметры критерия текучести Хука – Брауна (m_b0, s₀), но и на выражение начального угла дилатансии ψ₀^rm (верхний индекс rm обозначает состояние массива скальной породы). Эффект перехода от ненарушенной структуры образца к структуре массива скального грунта будет введен через скалярную величину ζ в соответствии с формулой, предложенной Алехано (Alejano) и др. [5] (ψ₀^rm ≡ ζψ₀^ir, где верхний индекс ir обозначает ненарушенный скальный грунт (intact rock)).

 

Ненарушенный скальный грунт

 В предложенной модели и потеря прочности, и развитие дилатантного поведения ненарушенного скального грунта не учитывают потенциальные диссипативные явления перед пиковой прочностью. По этой причине начальный угол дилатансии можно считать совпадающим с его пиковым значением (ψ₀^ir ≡ ζψ_peak^ir), которое можно использовать для расчета m_ψ0. Таким образом, вместо определения параметра m_ψ0 по экспериментальным данным можно использовать уравнения, предложенные в литературе для оценки угла дилатансии на пределе прочности, например выведенные Уолтоном (Walton) и Дидерихсом (Diederichs) [22]:

 

 

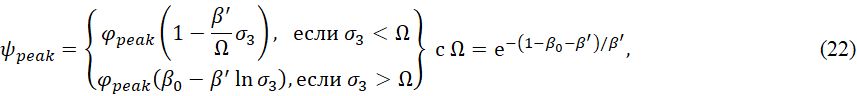
где β₀, β' – параметры, контролирующие чувствительность к боковому давлению для высоких и низких значений соответственно (для кристаллических пород рекомендуются значения β₀ = 1; β' = 0,1 [22]); φ_peak – угол внутреннего трения на пределе прочности. Теперь необходимо определить предельный угол внутреннего трения φ_peak, который может быть связан со свойствами материала модели Хука – Брауна [5]:

 

 

В уравнение (23) могут быть подставлены параметры ненарушенного скального грунта (α = 0,5; m_b ≡ m_i), что для его образцов приводит к следующей формуле:

 

 

Влияние на состояние массива скального грунта

 Чтобы скорректировать величину пикового угла дилатансии для трещиноватого скального грунта, значение ψ₀^rm рассчитывается на основе ψ₀^ir и скалярной величины ζ, которая выражается как функция геологического индекса прочности GSI [4, 8]. По этой причине была принята линейная зависимость от среднего угла дилатансии, предложенная Алехано (Alejano) и др. [5]:

 

 

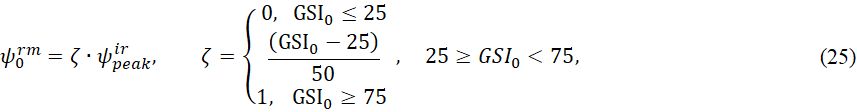
где ζ – коэффициент, учитывающий начальное состояние массива скального грунта, который определяется через GSI₀.

Уравнение (25) подчеркивает связь механических свойств скальных пород с протекающей дилатансией. Массивы скальных грунтов с низкой прочностью (например, имеющие GSI₀ < 25) характеризуются нулевой дилатансией, в то время как для скальных пород с высокой прочностью (GSI₀ > 75) значение угла дилатансии равно таковому для ненарушенной породы.

 

Функция, ограничивающая зону растяжения

 Чтобы ввести функцию, ограничивающую зону растягивающих напряжений, среднее напряжение на углу поверхности текучести Хука – Брауна снижается за счет параметра α, который находится в диапазоне от 0 до 1 (рис. 8):

 

 

 

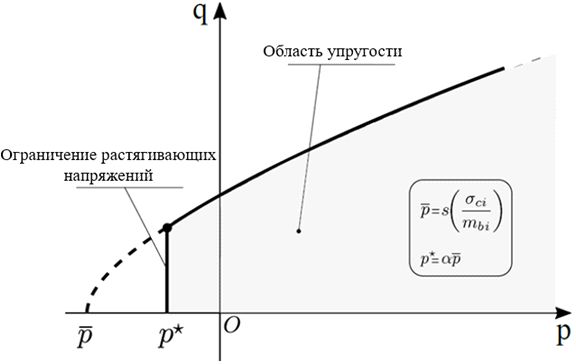
Для зоны растягивающих напряжений используется ассоциированный закон пластического течения (когда вектор пластической деформации в девиаторном пространстве направлен по нормали к поверхности текучести. – Ред.), который характеризуется механизмом идеально-пластического течения (то есть когда m_b ≡ m_b0; s₀ ≡ s). Пользователь может рассчитать величину α и соответствующее значение p*, исходя из предела прочности на растяжение σ_t, полученного по результатам лабораторных испытаний. Так, предел прочности на одноосное растяжение связан с соответствующим ему средним напряжением p^* и параметром α следующими уравнениями:

 

 

 Для ненарушенных скальных грунтов уравнение (27) принимает вид:

 

 

В рассматриваемой модели параметр α по умолчанию установлен равным 0,5.

 

Входные параметры для моделей HB_SSM и HB_GSM

 Для моделей HB_SSM и HB_GSM входными являются такие классические упругие параметры, как модуль деформации E и коэффициент Пуассона ν, а также предельная прочность ненарушенного скального грунта при отсутствии бокового давления (σ_ci), безразмерный параметр ненарушенной скальной породы m_i, геологический индекс прочности GSI, коэффициент нарушенности D (рис. 9–11; таблицы 1–5).

 

 

Таблица 1. Входные параметры для моделей HB_SSM и HB_GSM, полученные по результатам калибровки для скального грунта ненарушенной структуры

 

 

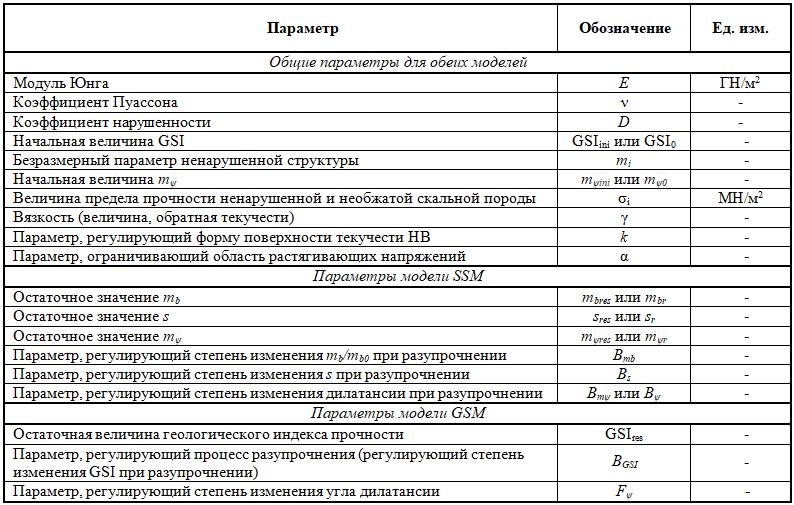
Таблица 2. Значения предельной прочности ненарушенного образца скального грунта при отсутствии бокового давления (σ_ci) для различных типов пород

 

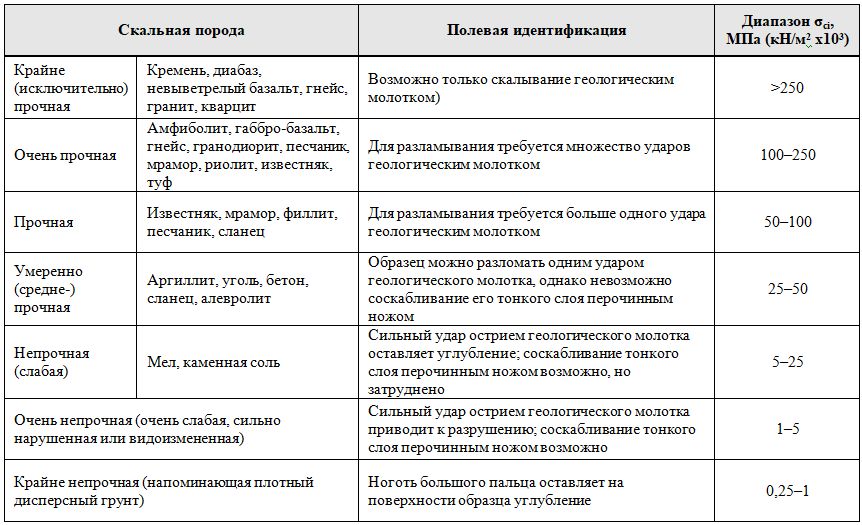
Таблица 3. Значения безразмерного параметра ненарушенного образца скальной породы m_i для различных типов скальных пород

 

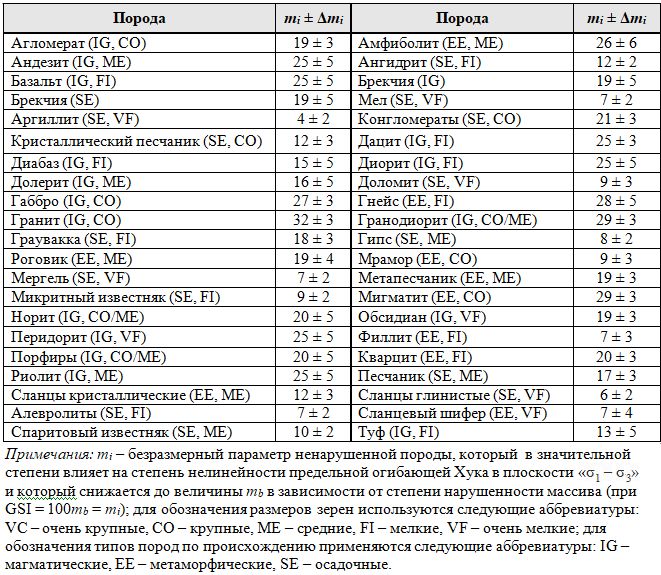
Таблица 4. Рекомендации по выбору коэффициента нарушенности массива пород D [3]

 

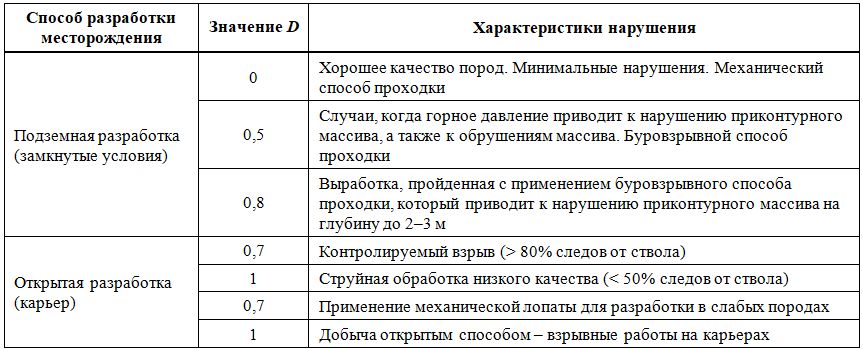
Таблица 5. Качественные показатели для определения коэффициента нарушенности массива пород D (см. рис. 10)

 

 

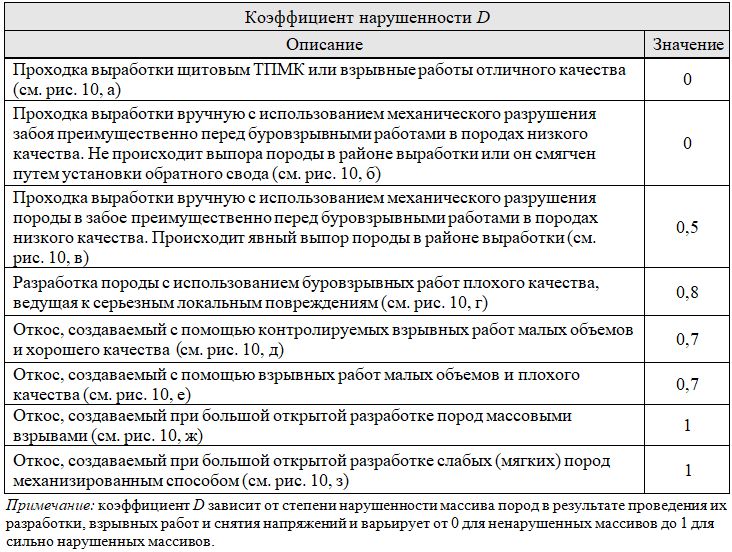
Что касается параметра γ (см. таблицу 1), то в обоих подходах (моделях HB_SSM и HB_GSM) он отражает вязкость (свойство материала, обратное текучести) и вводится для корректировки сетки конечных элементов при численном решении с локализацией деформаций. Величина γ определяет степень ползучести модели, устанавливая степень чувствительности механической реакции на воздействие. В контексте рассматриваемой модели параметр γ в том числе используется как «переключатель», позволяющий пользователю выбирать либо упругопластический, либо вязкопластический вариант модели или ее аналога в зависимости от скорости деформирования. При γ ≤ 0 модель является упругопластической (когда механическая реакция не зависит от времени), а при γ > 0 модель является вязкопластической (когда механическая реакция зависит от времени).

Введение вязкопластической функции способно моделировать не только зависящую от скорости деформирования механическую реакцию при быстром динамическом процессе, но и способствует регуляризации проблем краевых условий во время развития локализации деформации.

Параметры состояния модели могут быть отображены в программе вывода данных Plaxis Output при следующей последовательности выбора: Stresses → State parameters → User → User-defined parameters. Всего может быть выбрано четыре параметра состояния:

• ε_p^eq;
• m_b, s;
• m_ψ; 
• последний выбранный параметр используется внутренне, для инициализации задачи в начале вычисления.

 

Заключение

 

Автор обзора, составленного на основе адаптированного перевода руководства по использованию модели Хука – Брауна с разупрочнением (Hoek & Brown model with softening – HBS) [15] и дополнительной информации, надеется, что эта модель поможет российским специалистам значительно повысить качество прогнозов поведения массивов скальных пород в реальных условиях геотехнического строительства. Ведь точность таких прогнозов имеет огромное влияние на надежность и рациональность проектных решений (например, в отношении устойчивости забоя и прилегающего свода горной выработки, влияния выбранной технологии проходки на негативные геомеханические процессы во вмещающих грунтах, поведения подземных выработок при сейсмических нагрузках, правильности выбора параметров систем креплений котлованов, траншей или тоннелей, устойчивости незакрепленных обнажений скальных пород и даже, возможно, динамических проявлений горного давления в виде горных ударов). 

---

Список литературы

 

1. Бринкгреве Р. Работа в PLAXIS. Поведение скальных грунтов (перевод на рус. яз.) // ГеоИнфо. 08.07.2021. URL: geoinfo.ru/product/brinkgreve-ronald/rabota-v-plaxis-povedenie-skalnyh-gruntov-44941.shtml.
2. Бринкгреве Р., Кумарсвами С., Сволфс В.М., Фориа Ф. PLAXIS 3D. Руководство пользователя. М.: ООО «НИП-Информатика», 2017. 816 p.
3. Нгуен Ван Минь. Прогноз мощности зон растягивающих деформаций при проходке подготовительных горных выработок на глубине свыше 1 км: диссертационная работа. М: МИСиС, 2021. URL: misis.ru/files/19586/07.09.2021%20Диссертация.pdf.
4. Alejano  L., Alonso E. Considerations of the dilatancy angle in rocks and rock masses // International Journal of Rock Mechanics and Mining Sciences. 2005. Vol. 42. № 4. P. 481–507.
5. Alejano L., Alonso E., Rodrнguez-Dono A., Fernбndez-Manнn G. Application of the convergence confinement method to tunnels in rock masses exhibiting Hoek-Brown strain softening behavior // International Journal of Rock Mechanics and Mining Sciences. 2010. Vol. 47. № 1. P. 150–160.
6. Alonso E., Alejano L., Varas F., Fdez-Manin G., Carranza-Torres C. Ground response curves for rock masses exhibiting strain-softening behavior // International Journal for Numerical and Analytical Methods in Geomechanics. 2003. Vol. 27. № 13. P. 1153–1185.
7. Cai M., Kaiser P., Tasaka Y., Minami M. Determination of residual strength parameters of jointed rock masses using the GSI system // International Journal of Rock Mechanics and Mining Sciences. 2007. Vol. 44. № 2. P. 247–265.
8. Hoek E., Brown E.T. Practical estimates of rock mass strength // International Journal of Rock Mechanics and Mining Sciences. 1997. Vol. 34. № 8. P. 1165–1186.
9. Hoek E., Brown E.T. The Hoek-Brown failure criterion and GSI (2018 Edition) // Journal of Rock Mechanics and Geotechnical Engineering. 2019. Vol. 11. № 3. P. 445–463.
10. Hoek E., Carranza-Torres C., Corkum B. Hoek-Brown failure criterion (2002 edition) // Proceedings of the NARMS-TAC Conference, Toronto, 2002. Vol. 1. P. 267–271.
11. Jiang H. A failure criterion for rocks and concrete based on the Hoek-Brown criterion // International Journal of Rock Mechanics and Mining Sciences. 2017. Vol. 95. P. 62–72.
12. Jiang H., Zhao J. A simple three-dimensional failure criterion for rocks based on the Hoek-Brown criterion // Rock Mechanics and Rock Engineering. 2015. Vol. 48. № 5. P. 1807–1819.
13. Manouchehrian A., Cai M. Analysis of rockburst in tunnels subjected to static and dynamic loads // Journal of Rock Mechanics and Geotechnical Engineering. 2017. Vol. 9. № 6. P. 1031–1040.
14. Marinelli F., Buscarnera G. A generalized backward Euler algorithm for the numerical integration of a viscous breakage model // International Journal for Numerical and Analytical Methods in Geomechanics. 2019. Vol. 43. № 1. P. 3–29.
15. Marinelli F., Zalamea N., Brasile S., Brinkgreve R.B.J. An advanced Hoek & Brown model with softening: user manual. Delft: Plaxis bv, 2019. URL: communities.bentley.com/products/geotech-analysis/w/plaxis-soilvision-wiki/46245/udsm---hoek-brown-model-with-softening.
16. Marinelli F., Zalamea N., Vilhar G., Brasile S., Cammarata G., Brinkgreve R. Modeling of brittle failure based on Hoek & Brown yield criterion: parametric studies and constitutive validation // Proceedings of the 53rd US Rock Mechanics/Geomechanics Symposium, 2019.
17. Marinos V., Marinos P., Hoek E. The geological strength index: applications and limitations // Bulletin of Engineering Geology and the Environment. 2005. Vol. 64. № 1. P. 55–65.
18. Perzyna P. Fundamental problems in viscoplasticity //Advances in Applied Mechanics. 1966. Vol. 9. P. 243–377.
19. Ranjbarnia M., Fahimifar A., Oreste P. Analysis of non-linear strain-softening behaviour around tunnels // Proceedings of the Institution of Civil Engineers. Geotechnical Engineering. 2015. Vol. 168. № 1. P. 16–30.
20. Ribacchi R. Mechanical tests on pervasively jointed rock material: insight into rock mass behavior // Rock Mechanics and Rock Engineering. 2000. Vol. 33. № 4. P. 243–266.
21. Vermeer P.A., De Borst R. Non-associated plasticity for soils, concrete and rock. HERON, 1984. Vol. 29. № 3.
22. Walton G., Diederichs M. A new model for the dilation of brittle rocks based on laboratory compression test data with separate treatment of dilatancy mobilization and decay // Geotechnical and Geological Engineering. 2015. Vol. 33. № 3. P. 661–679.
23. Zou J.-f., Zuo S.-Q., Xu Y. Solution of strain-softening surrounding rock in deep tunnel incorporating 3D Hoek-Brown failure criterion and flow rule // Hindawi. Mathematical Problems in Engineering. 31.07/2016. Vol. 2016. Article ID 7947036. DOI: https://doi.org/10.1155/2016/7947036. URL: hindawi.com/journals/mpe/2016/7947036/.