Дискретно-элементное моделирование влияния формы частиц на ползучесть каменной наброски

ВВЕДЕНИЕ

Каменные наброски с прошлого века широко используются в гражданском строительстве, например при создании плотин, железных дорог и фундаментов аэропортов в горных районах. Большое количество полевых наблюдений показало, что механическое поведение каменных набросок зависит от времени, а их осадки после строительства продолжаются в течение многих десятилетий [1, 2]. Широко признано, что основной причиной ползучести каменной наброски является разрушение частиц. Было приложено много усилий и лабораторных испытаний образцов каменных набросок для изучения влияния размеров, прочности и формы частиц, содержания воды и уровня напряжений [3]. Однако микроскопический механизм ползучести каменной наброски до сих пор остается малоизученным.

По сравнению с физическими экспериментами моделирование методом дискретных элементов (МДЭ) дает возможность наблюдать и контролировать микроскопическое поведение каменной наброски на уровне отдельных частиц. С учетом того, что разрушение частиц является основной причиной ползучести каменных набросок, имеется два основных способа их моделирования:

1. использование разрушаемого скрепленного кластера для моделирования частицы [4];
2. замена исходного неразрушаемого диска или комка на набор дисков или комков меньшего размера [5, 6].

Чтобы смоделировать зависящее от времени поведение каменной наброски, в работе [7] была разработана модель на основе МДЭ, в которой зерна задаются как комки из скрепленных более мелких частиц, а критерием их разрушения является субкритическое распространение в них трещин.

В работах [8, 9] была смоделирована ползучесть каменной наброски c включением в метод механики поведения материальных точек (частиц) моделей старения связей между ними, уменьшения либо прочности параллельных связей, либо диаметра связей.

Результаты вышеупомянутых исследований продемонстрировали, что с помощью МДЭ на основе поведения частиц можно моделировать поведение ползучести каменной наброски.

В недавних работах [10, 11] было исследовано влияние на ползучесть каменных набросок со стороны гидрологических условий и уровня напряжений.

Такая важная характеристика, как форма частиц, редко изучалась на предмет ее влияния на поведение каменной наброски. Авторы публикации [12] изучали влияние формы частиц на пиковую прочность каменной наброски с помощью 3D моделирования с использованием МДЭ. Однако в предыдущих исследованиях не сообщалось о влиянии формы частиц на ползучесть набросок.

Основная цель данной статьи – изучение влияния формы частиц на ползучесть каменной наброски при разных граничных условиях.

МЕТОДЫ ИССЛЕДОВАНИЯ

В этой работе для двумерного моделирования поведения каменных набросок использовалась коммерческая программа Particle Flow Code 2D (PFC 2D) версии 2008 года, разработанная компанией Itasca. Чтобы имитировать разрушение частиц, обломки скального грунта можно представить в виде кластеров, состоящих из ряда еще более мелких частиц, связанных друг с другом. Использовались параллельные связи с учетом усилий на контактах и моментов в кластере.

Каждая параллельная связь имеет пять параметров: нормальную и сдвиговую жесткость, нормальную и сдвиговую прочность и радиус. Как только нормальное или сдвиговое напряжение превышает прочность связи, она разрывается и появляется микротрещина. Более подробную информацию об использованной модели связей можно найти в публикации [13].

Для моделирования ползучести каменной наброски из-за дробления частиц в работах [8, 9, 14, 15] было предложено несколько моделей старения связей. По мнению авторов публикации [10], все эти модели можно использовать для имитации ползучести каменной наброски с соответствующими эмпирическими параметрами.

В представленном в настоящей статье исследовании использовалась модель старения связей, предложенная авторами работы [8], то есть снижение прочности параллельных связей со временем. Математические выражения для этой модели таковы:

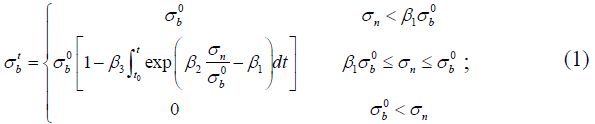
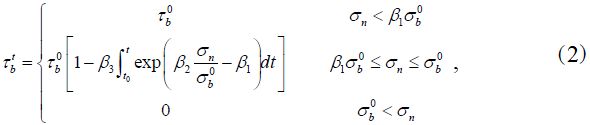
где σ_b⁰, σ_b^t – соответственно кратковременная и долговременная прочность при сжатии/растяжении (нормальная прочность); τ_b⁰, τ_b^t – соответственно кратковременная и долговременная прочность при сдвиге (сдвиговая прочность); β₁, β₂, β₃ – три эмпирических параметра, которые зависят от размера частиц, их формы и свойств материала. Параметр β₁ «контролирует» величину напряжения активации. Если приложенное нормальное напряжение σ_n ниже напряжения активации β₁σ_b⁰, то снижение прочности не активируется. Если σ_n больше напряжения активации β₁σ_b⁰, но меньше кратковременной прочности, то снижение прочности активируется и тогда прочность параллельной связи уменьшается со временем согласно приведенным выше уравнениям. Когда σ_n превышает кратковременную прочность, то параллельная связь разрывается и появляется микротрещина. В этом исследовании временной шаг при расчете деградации связи был постоянным и составлял 100 секунд.

МОДЕЛИРОВАНИЕ

Модельные квадратные образцы имели исходную длину стороны 200 мм. Были использованы две разные формы составляющих их частиц – округлая (предложенная в работе [10]) и угловатая (предложенная в публикации [11]) (рис. 1). Если условно назвать наибольшее расстояние между двумя точками частицы ее диаметром, то диапазон диаметров как округлых, так и угловатых частиц составил 6,82 –11,18 мм (в среднем – 9,18 мм). При начальной пористости 0,3 в модели было сгенерировано 120 округлых и 213 угловатых частиц. Основные модельные микропараметры приведены в таблице. Более подробную информацию об имитации образцов можно найти в публикациях [10, 11].

Рис. 1. Примеры смоделированных образцов каменной наброски из округлых (а) и угловатых (б) частиц

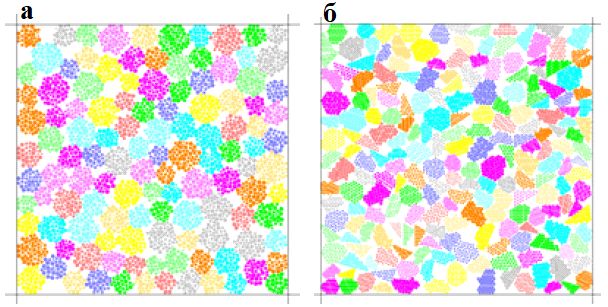
Таблица. Микропараметры модельных образцов каменной наброски

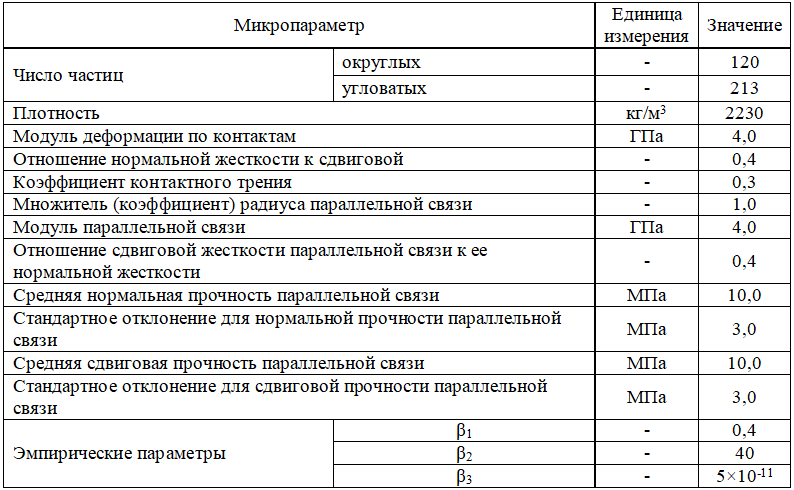
После генерации образцов были смоделированы испытания на одноосное сжатие и на прямой сдвиг.

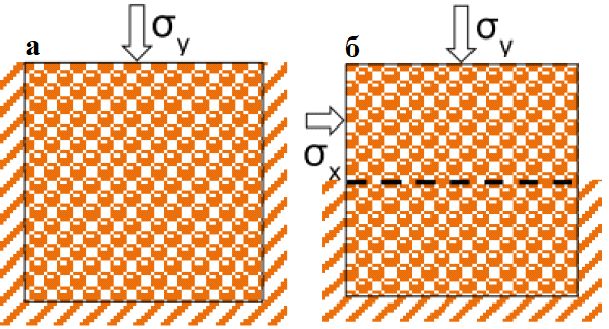
Во время одноосного сжатия боковые стенки и уровень дна были зафиксированы, в то время как верхняя поверхность перемещалась вниз с определенной скоростью для достижения желаемого уровня напряжения (рис. 2, а). Для автоматического поддержания постоянного нормального напряжения во время развития процесса ползучести в образце использовался сервоалгоритм.

Для испытания на прямой сдвиг требуемые нормальные и сдвиговые напряжения были достигнуты путем перемещения верхнего бокса установки (рис. 2, б). Затем напряжения поддерживались постоянными с помощью сервоалгоритма. Нижний бокс был зафиксирован на протяжении всего процесса. После начала моделирования ползучести в течение всего испытания контролировались цепочки усилий, разрушение частиц каменной наброски и деформации образца.

Рис. 2. Разные граничные условия при модельных испытаниях на одноосное сжатие (а) и на прямой сдвиг (б)

РЕЗУЛЬТАТЫ МОДЕЛИРОВАНИЯ

Испытания на одноосное сжатие

Нормальные напряжения, приложенные при одноосном сжатии, составляли 400, 600, 800, 1000 и 1140 кПа. Было сгенерировано 6 образцов из округлых частиц и 8 – из угловатых при различных упаковках (распределении частиц) и прочностях связей, которые были созданы путем изменений начального значения генератора случайных чисел.

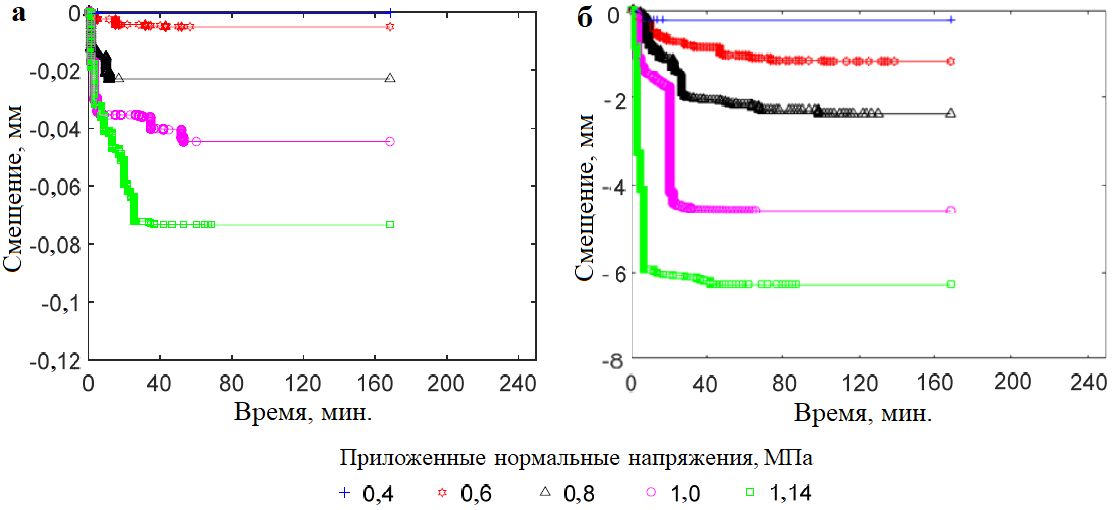
На рисунке 3 показаны типичные кривые ползучести (изменения смещений во времени) при каждом постоянном нормальном напряжении для модельных образцов каменной наброски с округлыми (а) и угловатыми (б) частицами. В обоих случаях происходило увеличение нормального смещения при росте приложенного нормального напряжения. По сравнению с образцами с округлыми частицами образцы с угловатыми частицами испытывали более сильные деформации ползучести при таком же нормальном напряжении.

Рис. 3. Деформирование модельных образцов каменной наброски с округлыми (а) и угловатыми (б) частицами при одноосном сжатии

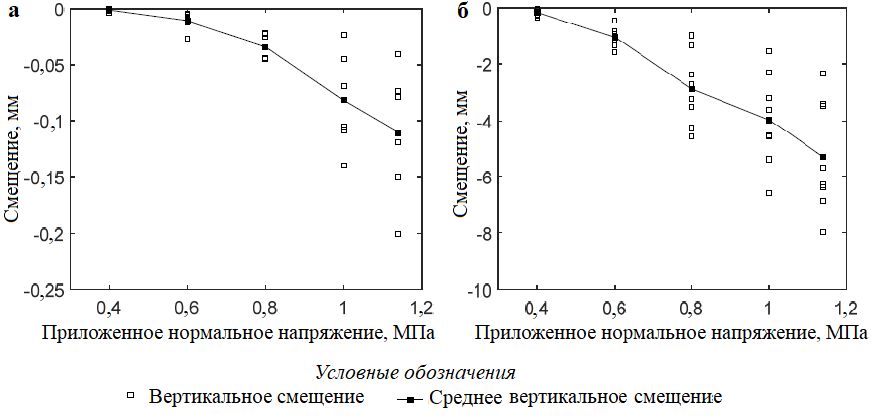
На рисунке 4 сопоставлены нормальные смещения через 10 тысяч секунд воздействия приложенных напряжений. Как округлые, так и угловатые частицы показали увеличение среднего нормального смещения при возрастании приложенного напряжения. Однако приращения для образцов с угловатыми частицами были более значительными.

Рис. 4. Деформации ползучести при одноосном сжатии модельных образцов каменной наброски с округлыми (а) и угловатыми (б) частицами через 10 тысяч секунд приложения того или иного нормального напряжения

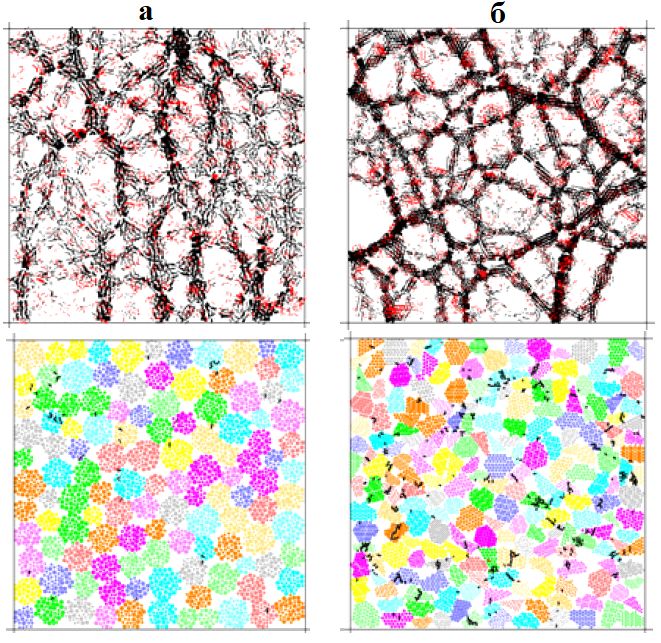
На рисунке 5 показаны примеры распределений сил связи (сцепления) и микротрещин при нормальном напряжении 0,8 МПа. Образцы с угловатыми частицами имели более неравномерное распределение сил и подвергались большему количеству разрушений, чем образцы с округлыми частицами, что могло быть причиной более сильных нормальных смещений для образцов с угловатыми частицами.

Рис. 5. Распределение сил связей (сцепления) и микротрещин при одноосном сжатии образцов каменной наброски с округлыми (а) и угловатыми (б) частицами

Испытания на прямой сдвиг

В случае испытания на прямой сдвиг к верхнему боксу установки прикладывалось постоянное нормальное напряжение 1,14 МПа. Напряжение сдвига варьировало от 0,2 до 0,6 МПа (интервал составлял 0,1 МПа). Как и в предыдущем случае, было смоделировано 6 образцов с округлыми частицами и 8 – с угловатыми с различными упаковками (распределением частиц) и прочностью связей (сцепления).

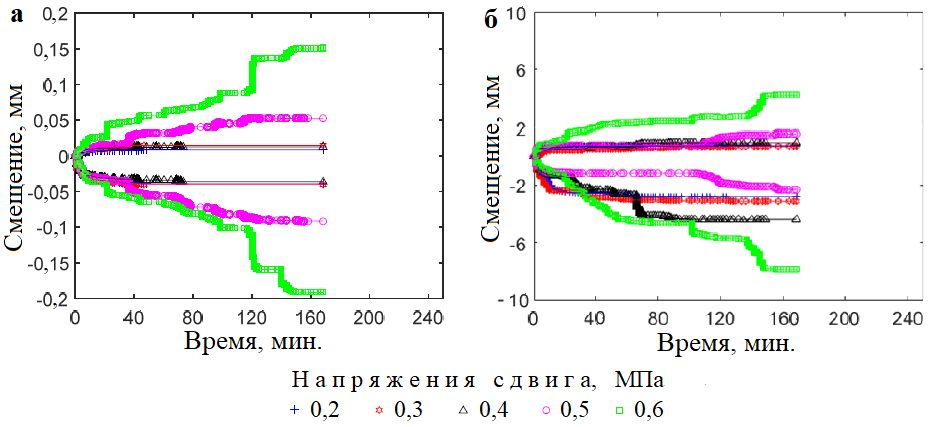
На рисунке 6 представлены типичные кривые развития смещений во времени при различных напряжениях сдвига. Характеристики деформаций сильно зависели от напряжения сдвига и формы частиц. Если напряжение сдвига было низким, то как нормальные, так и сдвиговые смещения быстро увеличивались, а затем оставались почти постоянным, что можно рассматривать как фазы первичной и вторичной ползучести. При высоком сдвиговом напряжении нормальные смещения были более значительными, чем сдвиговые. При этом как нормальные, так и сдвиговые смещения увеличивались с ростом напряжения сдвига. Однако приращения сдвигового смещения для образцов с округлыми частицами были более значительными.

Рис. 6. Деформации образцов каменной наброски с округлыми (а) и угловатыми (б) частицами при испытаниях на прямой сдвиг

На рисунке 7 показаны примеры распределения сил связи (сцепления) и микротрещин через 10 тысяч секунд при сдвиговом напряжении 0,5 МПа. В образце с закругленными частицами силы сцепления были статистически более равномерно распределены, а микротрещины образовывались преимущественно «в углах» частиц. Однако в образце с угловатыми частицами появилось больше микротрещин, а фрагментация (дробление) частиц была более полной.

Рис. 7. Распределение сил связи (сцепления) и микротрещин в образцах каменной наброски с округлыми (а) и угловатыми (б) частицами при испытании на прямой сдвиг при напряжении сдвига 0,5 МПа

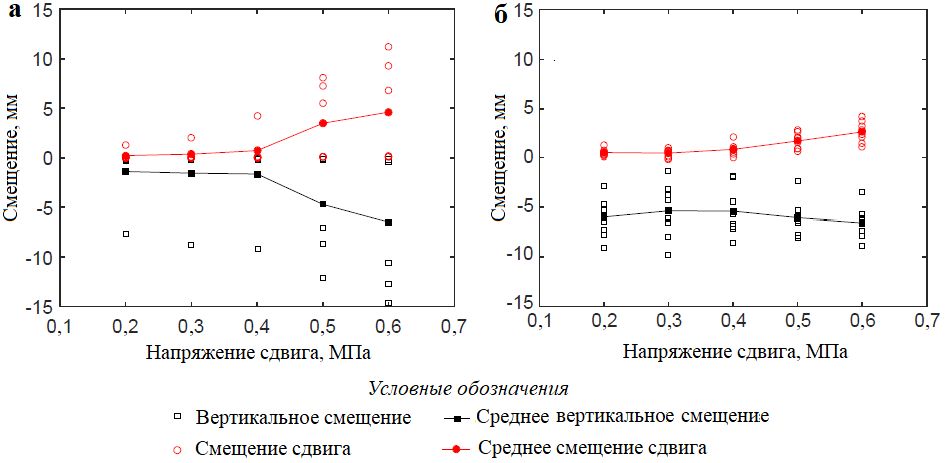
Результаты испытаний на прямой сдвиг через 10 тысяч секунд представлены на рисунке 8. Как округлые, так и угловатые частицы показали увеличение среднего смещения сдвига при росте сдвигового напряжения. Однако среднее нормальное смещение, которое указывает на вызванное сдвигом сжатие (дилатансию), не проявило аналогичной тенденции для округлых и угловатых частиц. Среднее нормальное смещение угловатых частиц было почти постоянным с увеличением напряжения сдвига, тогда как нормальное смещение округлых частиц значительно возрастало с ростом напряжения сдвига. Можно полагать, что в процессе ползучести округлых частиц важную роль играет ключевая частица.

Рис. 8. Деформации ползучести при модельных образцов каменной наброски с округлыми (а) и угловатыми (б) частицами при испытании на прямой сдвиг через 10 тысяч секунд приложения сдвигового напряжения

В цепочке усилий в качестве ключевой может быть определена частица, разрушение которой может вызвать цепную реакцию, в конечном итоге приводящую к разрушению образца. На рисунке 9 показаны случаи того, как она работает в образце с округлыми частицами в процессе развития ползучести. Через 10 минут цепочка усилий была стабильна и появилось небольшое количество микротрещин. Через 30 минут возникла полная фрагментация, однако смещения все еще были небольшими, то есть образец еще оставался устойчивым. Через 40 минут разрушилась ключевая частица, что привело к смене цепочек усилий и в результате – к многочисленным разрушениям в следующие 10 минут.

Рис. 9. Изменения в распределении сил связи и микротрещин в процессе испытания на прямой сдвиг образца с округлыми частицами при сдвиговом напряжении 0,5 МПа. Ключевая частица обведена черным овалом

ВЫВОДЫ

Было исследовано влияние формы частиц на ползучесть образцов каменных набросок с различными граничными условиями с помощью численного моделирования с использованием метода дискретных элементов. Для моделирования развития ползучести образцов была использована модель старения связей (сцепления), предложенная в работе [8]. Приведем основные выводы.

1. При одноосном сжатии нормальные смещения увеличивались при возрастании нормального напряжения. Смещения для образцов с угловатыми частицами были более значительными.

2. При испытании на прямой сдвиг как нормальные, так и сдвиговые смещения ползучести округлых частиц были больше, чем в случае угловатых частиц.

3. Ключевая частица была выявлена в образцах как с округлыми, так и с угловатыми частицами. Однако при округлых частицах она играла более важную роль.

-

Это исследование было финансово поддержано Национальной программой фундаментальных исследований Китая (Программой 973, № контракта: 2014CB047003).

ИСТОЧНИК ДЛЯ ПЕРЕВОДА

Wang Yu., Zhao Zh., Song E. Discrete element modeling of the effect of particle shape on creep behavior of rockfills // International Journal of Geological and Environmental Engineering. WASET, 2017. Vol. 11. № 9. DOI: doi.org/10.5281/zenodo.1132286. URL: publications.waset.org/10007963/discrete-element-modeling-of-the-effect-of-particle-shape-on-creep-behavior-of-rockfills; publications.waset.org/10007963/pdf.

СПИСОК ЛИТЕРАТУРЫ, ИСПОЛЬЗОВАННОЙ АВТОРАМИ ПЕРЕВЕДЕННОЙ СТАТЬИ

1. Sowers G.F., Williams R.C., Wallace T.S. Compressibility of broken rock and the settlement of rockfills // Proceedings of the 6th ICSMFE. 1965. Vol. 2. P. 561–565.
2. Marsal R.J., Arellano L.R., Guzman M.A., Adame H. Infernillo: behavior of dams built in Mexico. Mexico: Instituto de Ingenierнa, UNAM, 1976.
3. Oldecop L., Alonso E. Theoretical investigation of the time-dependent behaviour of rockfill // Geotechnique. 2007. Vol. 57. № 3. P. 289–301.
4. Cheng Y.P., Nakata Y., Bolton M.D. Discrete element simulation of crushable soil // Geotechnique. 2003. Vol. 53. № 7. P. 633–642.
5. McDowell G.R., de Bono J.P. On the micro mechanics of one-dimensional normal compression // Geotechnique. 2013. Vol. 63. № 11. P. 895. DOI:10.1680/geot.12.P.041.
6. Tapias M., Alonso E.E., Gili J. A particle model for rockfill behaviour // Geotechnique. 2015. Vol. 65. № 12. P. 975–994.
7. Alonso E.E., Tapias M., Gili J. Scale effects in rockfill behaviour // Geotechnique Letters. 2012. Vol. 2. № 3. P. 155–160.
8. Tran T.H., Venier R., Cambou B. Discrete modelling of rock-ageing in rockfill dams // Computers and Geotechnics. 2009. Vol. 36. № 1. P. 264–275.
9. Potyondy D.O. Simulating stress corrosion with a bonded-particle model for rock // International Journal of Rock Mechanics and Mining Sciences. 2007. Vol. 44. № 5. P. 677–691.
10. Zhao Z., Song E.X. Particle mechanics modeling of creep behavior of rockfill materials under dry and wet conditions // Computers and Geotechnics. 2015. Vol. 68. P. 137–146.
11. Zhou M., Song E. A random virtual crack DEM model for creep behavior of rockfill based on the subcritical crack propagation theory // Acta Geotechnica. 2016. Vol. 11. № 4. P. 827–847.
12. Zhou W., Ma G., Chang X., Zhou C. Influence of particle shape on behavior of rockfill using a three-dimensional deformable DEM // Journal of Engineering Mechanics. 2013. Vol. 139. № 12. P. 1868–1873.
13. Potyondy D.O., Cundall P.A. A bonded-particle model for rock // International journal of rock mechanics and mining sciences.2004. Vol. 41. № 8. P. 1329–1364.
14. Silvani C., Desoyer T., Bonelli S. Discrete modelling of time-dependent rockfill behaviour // International journal for numerical and analytical methods in Geomechanics. 2009. Vol. 33. № 5. P. 665–685.
15. Kwok C.Y., Bolton M.D. DEM simulations of soil creep due to particle crushing // Geotechnique. 2013. Vol. 63. № 16. P. 1365–1376.