Исследования озерных глин с использованием самозабуривающегося прессиометра на озере Тайху (Китай). Часть 3
 Ван Бинь (Wang Bin)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов (г. Ухань) и Университет Китайской академии наук (г. Пекин), Китайbwang@whrsm.ac.cn
Ван Бинь (Wang Bin)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов (г. Ухань) и Университет Китайской академии наук (г. Пекин), Китайbwang@whrsm.ac.cn Лю Кан (Liu Kang)Колледж гражданского строительства при Технологическом университете Хэфэя, г. Хэфэй, Китай k.liu@hfut.edu.cn
Лю Кан (Liu Kang)Колледж гражданского строительства при Технологическом университете Хэфэя, г. Хэфэй, Китай k.liu@hfut.edu.cn Ван Юн (Wang Yong)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов, г. Ухань, Китай yongwang93@163.com
Ван Юн (Wang Yong)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов, г. Ухань, Китай yongwang93@163.com  Цзян Цюань (Jiang Quan)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов (г. Ухань) и Университет Китайской академии наук (г. Пекин), Китай qjiang@whrsm.ac.cn
Цзян Цюань (Jiang Quan)Главная государственная лаборатория геомеханики и инженерно-геотехнических работ Уханьского института механики горных пород и грунтов (г. Ухань) и Университет Китайской академии наук (г. Пекин), Китай qjiang@whrsm.ac.cn  Бершов Алексей Викторовичгенеральный директор ГК «ПЕТРОМОДЕЛИНГ», преподаватель кафедры инженерной геологии Геологического факультета МГУ имени М.В. Ломоносоваalexey.bershov@petromodeling.com
Бершов Алексей Викторовичгенеральный директор ГК «ПЕТРОМОДЕЛИНГ», преподаватель кафедры инженерной геологии Геологического факультета МГУ имени М.В. Ломоносоваalexey.bershov@petromodeling.comПо инициативе и при поддержке ООО «Петромоделинг» редакция журнала «ГеоИнфо» продолжает знакомить читателей с прессиометрическими испытаниями грунтов. Данная группа методов большинством изыскателей и проектировщиков воспринимается просто как «более дешевая и простая альтернатива штамповых испытаний». На деле же это уникальные методы испытаний грунтов в массивах. Они используются для определения как действующих горизонтальных напряжений и коэффициента горизонтального давления грунта в состоянии покоя К0 (без которого, как известно, невозможны оценка начального (природного) состояния геологической среды и дальнейшие расчетные обоснования конструкций), так и физико-механических откликов геологической среды на горизонтальные механические воздействия, например зависимостей между напряжениями и деформациями, а также прочности на сдвиг в недренированных условиях.
Понимание методов оценки напряженно-деформированного состояния грунтового массива очень важно для эффективного перехода к трехмерному моделированию геологической среды и построению ее инженерных цифровых моделей – базовой части информационной цифровой модели объекта капитального строительства, без которой любые информационные проектные построения просто «повисают в воздухе».
Предлагаем вниманию читателей третью часть немного сокращенного адаптированного перевода статьи «Исследования озерных глин с использованием самозабуривающегося прессиометра на озере Тайху (Китай)» (ссылка на первоисточник имеется в конце). В этой части будут рассмотрены оставшиеся результаты испытаний, выполненных авторами переведенной работы. Отметим, что нумерация рисунков, формул и таблиц, соответствующая оригиналу, продолжит начатую в предыдущих частях.
Техническая правка выполнена генеральным директором ГК «Петромоделинг» Алексеем Бершовым.
РЕЗУЛЬТАТЫ ИСПЫТАНИЙ САМОЗАБУРИВАЮЩИМСЯ ПРЕССИОМЕТРОМ (продолжение)
Горизонтальное напряжение in situ
Одной из основных задач испытаний самозабуривающимся прессиометром является измерение горизонтального напряжения in situ. Если принять, что во время введения зонда SBPM не возникает нарушений окружающего грунта, то при достижении прессиометром определенной глубины давление, действующее на мембрану его рабочей камеры, равно горизонтальному давлению in situ (σh0). На рисунке 8, a представлены полученные значения σh0. Видна тенденция к их увеличению с глубиной. Стоит отметить, что нет существенной разницы между данными для трех скважин при глубине менее 17 м, но имеются явные различия между ними при глубине более 17 м.
Используя эффективное горизонтальное напряжение σ'h0, которое можно рассчитать по значению σh0 (см. рис. 8), и эффективное вертикальное напряжение σ'v0, можно получить коэффициент бокового (горизонтального) давления грунта в состоянии покоя K0 = σ'h0/σ'v0 (рис. 8, б). На рисунке 8, б для точек измерения в скважине 3 у поверхности грунта показаны чрезвычайно большие значения, что может быть связано с транспортными нагрузками от работающей поблизости строительной техники. В целом, и здесь результаты прессиометрических испытаний в трех скважинах довольно близки друг к другу при глубине менее 17 м, в то время как разница в значениях K0 заметнее при глубине более 17 м.
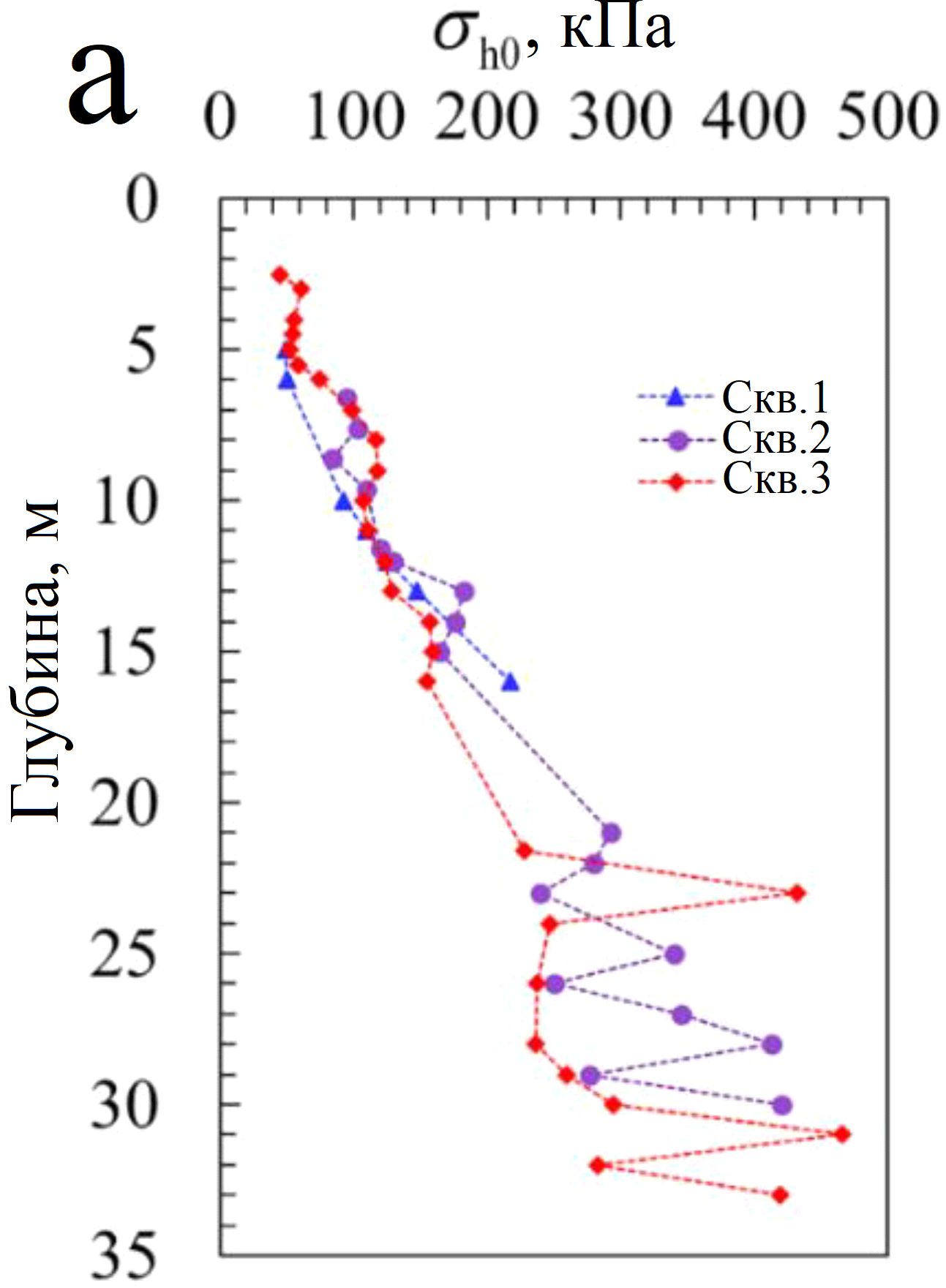
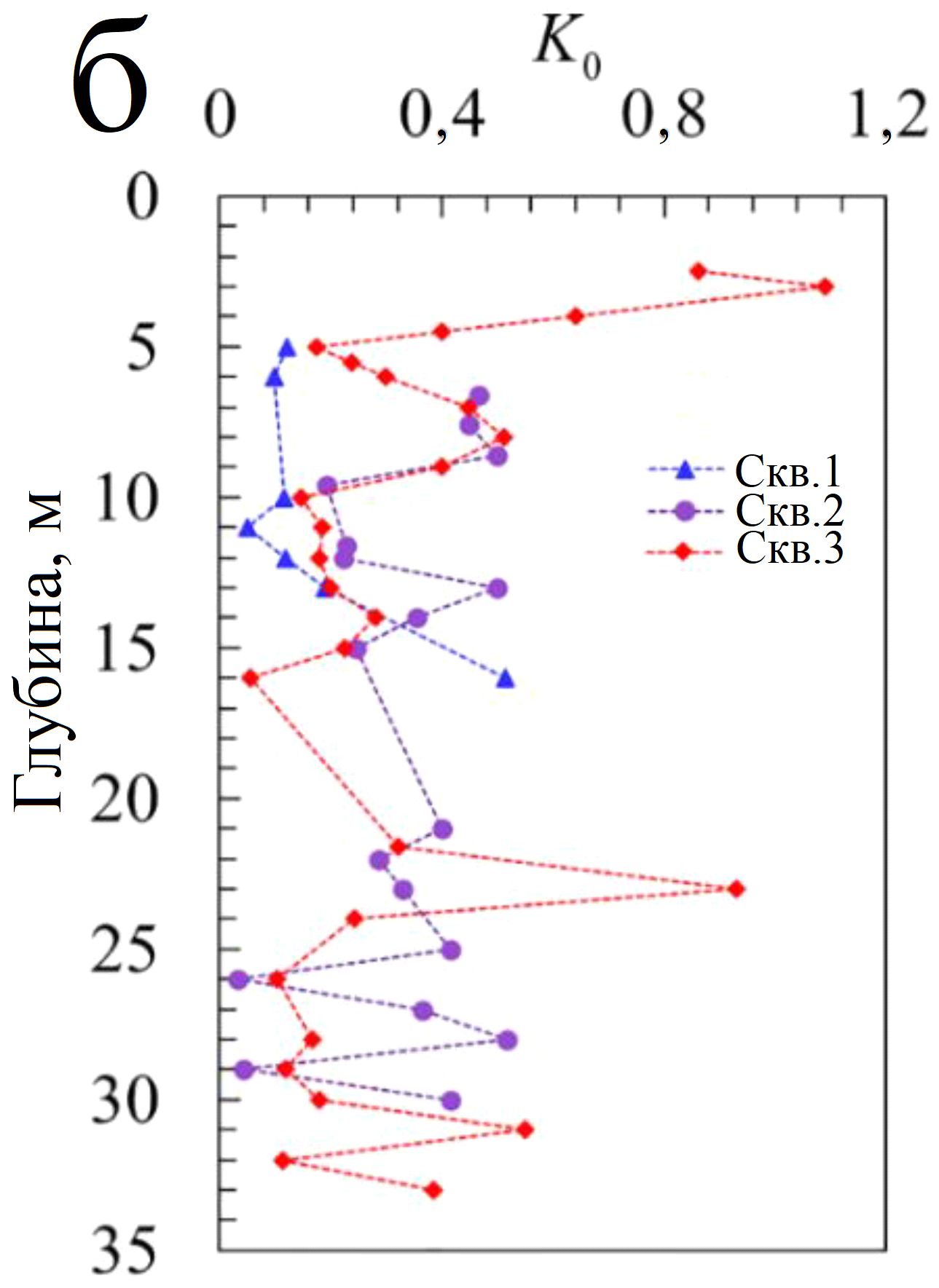
Рис. 8. Распределение по глубине исходного горизонтального напряжения σh0 (а) и коэффициента бокового давления грунта в состоянии покоя K0 = σ'h0/σ'v0 (б)
Модуль сдвига
Уменьшение модуля сдвига
На рисунке 9 схематично представлены изменения модуля сдвига с деформацией. Он обычно считается постоянным, когда порядок сдвиговой деформации очень мал, однако по мере дальнейшего увеличения деформации модуль быстро уменьшается и в конце концов опять становится постоянным. Поэтому для количественного анализа изменений модуля сдвига по глубине на разных стадиях были собраны и представлены в графическом виде максимальный (Gmax) и остаточный (Gres) модули сдвига, соответствующие наименьшей и наибольшей сдвиговым деформациям при испытаниях самозабуривающимся прессиометром для каждой точки зондирования (рис. 9, 10). Для сравнения на рисунке 10 также показаны величины модуля для цикла «разгрузка – повторное нагружение» (Gur).
![Рис. 9. Изменения модуля сдвига (жесткости) в зависимости от сдвиговой деформации (по [19])](/images/dynamic/img47145.jpg)
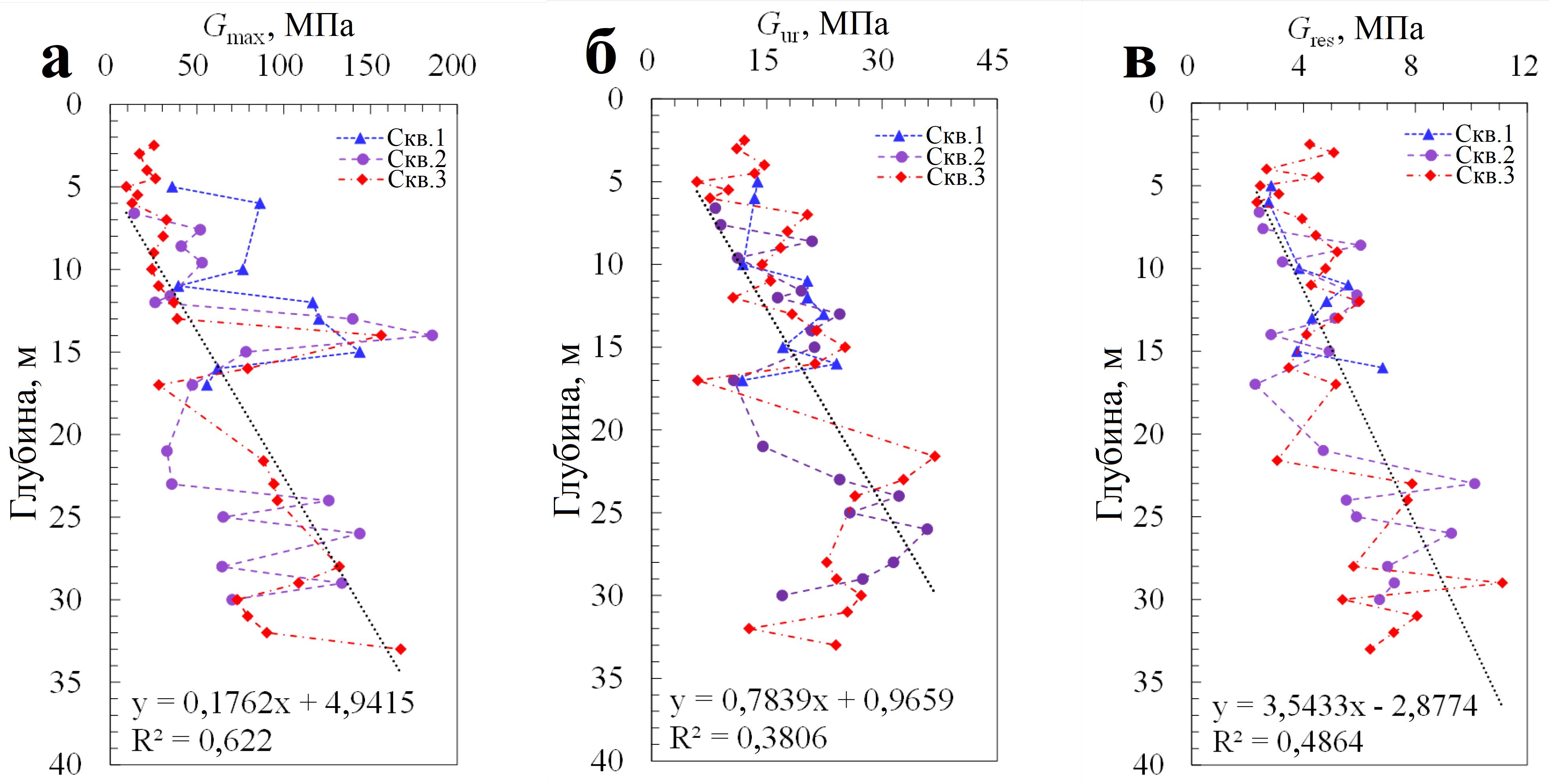
Рис. 10. Распределение по глубине максимального модуля сдвига Gmax (а), модуля для цикла «разгрузка – повторное нагружение» Gur (б) и остаточного модуля сдвига Gres (в)
На рисунке 10 видна общая тенденция к увеличению модуля сдвига с глубиной. Значения Gmax находятся в пределах 9,3–185,6 МПа, Gres – в диапазоне 2,8–12,0 МПа. А величины Gur попадают в пределы 6,0–46,9 МПа, что в целом находится между диапазонами Gmax и Gres. Также, видя тенденцию к увеличению с глубиной различий в откликах грунтов при испытаниях, можно сделать вывод, что гетерогенность озерных глинистых отложений озера Тайху с ростом глубины увеличивается.
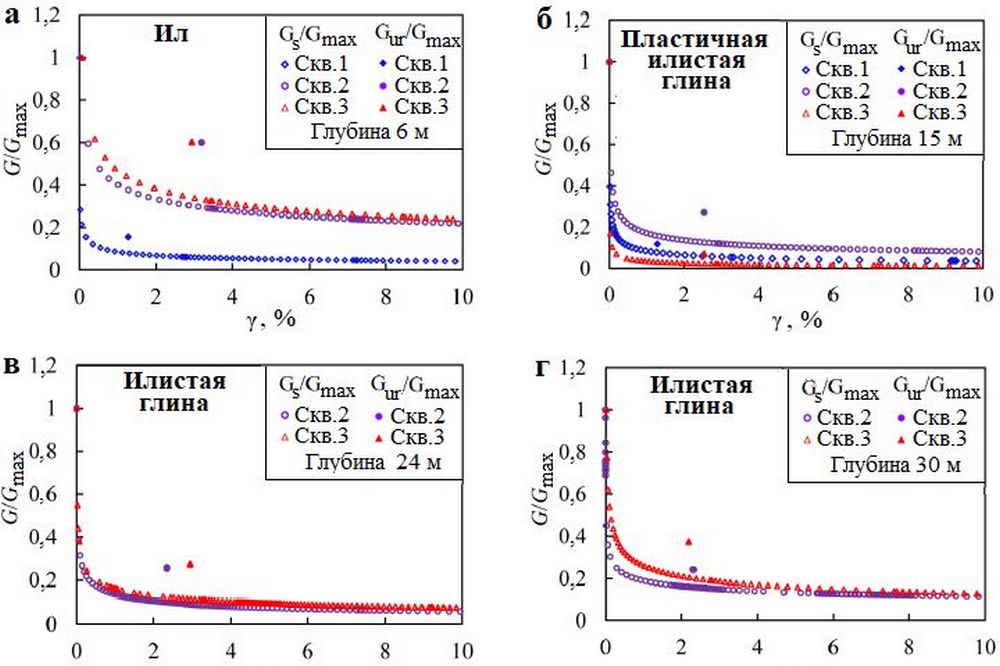
Для детального изучения деградации характеристик каждого типа грунта были выбраны четыре типичных примера. На рисунке 11 в графическом виде показаны зависимости между нормализованным модулем сдвига Gs/Gmax и сдвиговой деформацией. Для сравнения также приведены значения нормализованного модуля сдвига для цикла «разгрузка – повторное нагружение» (Gur/Gmax). Видно, что, во-первых, модуль уменьшается с увеличением деформации и, как правило, стабильное состояние может быть достигнуто при деформации сдвига γ > 1%. Кроме того, величины Gur/Gmax обычно соответствуют диапазону деформаций 1,0–3,2%. Показано, что в отличие от нелинейного модуля, соответствующего тем же деформациям, все линейные модули располагаются над кривыми, при этом различия между ними постепенно уменьшаются по мере увеличения деформации. Это может означать, что, когда деформация сдвига относительно невелика при прямом использовании Gur, оценка безопасности структуры будет завышенной.
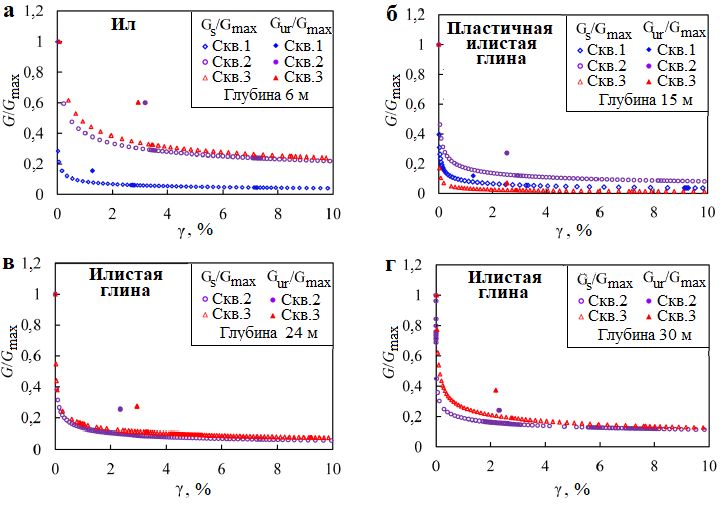
Рис. 11. Зависимости между нормализованным модулем сдвига и относительной деформацией γ (равной относительному изменению объема рабочей камеры самозабуривающегося прессиометра ΔV/V) для различных типов грунтов и разной глубины испытаний
Кроме того, сравнивая рисунки 11, а–г, также можно обнаружить, что наиболее резкое снижение модуля сдвига наблюдается в пластичной илистой глине, где он быстро уменьшается в очень небольшом диапазоне увеличения деформации. Кроме того, в этом грунте остаточный модуль сдвига Gres является самым низким по сравнению с другими типами исследованных отложений. При суммировании значений Gres для разных типов грунтов было установлено, что они находятся в пределах от 0,01 до 0,24. Для ила (при сходимости решения) они попадают в диапазон 0,04–0,24, для пластичной илистой глины – в диапазон 0,01–0,08, для илистой глины – в пределы 0,08–0,23. Диапазон этого модуля для пластичной илистой глины явно ниже, чем для ила и илистой глины, что может указывать на относительно более высокую структурную целостность пластичной илистой глины. Что касается расхождений между кривыми, представленными на рисунке 11, а, то это может быть связано со скоплением в илистом слое довольно большого количества раковин двустворчатых моллюсков (как это и было замечено при полевых исследованиях).
Влияние деформации на распределение значений секущего модуля сдвига
Как уже говорилось ранее, секущий модуль изменяется в зависимости от деформации сдвига. Поэтому для оценки влияния сдвиговой деформации на модуль сдвига берутся и представляются в графическом виде изменения с глубиной секущего модуля сдвига Gs при различных сдвиговых деформациях γ, равных 0,05; 0,1; 0,5; 1; 5% (на рисунке 12 для обозначения модуля сдвига используются соответствующие этим величинам нижние индексы). Для изучения тенденции к увеличению секущего модуля сдвига при сдвиговой деформации n получают его нормализованные значения по отношению к глубине:

где Gs,n – модуль сдвига, измеренный на определенной глубине при сдвиговой деформации n; Gmax,n, Gres,n – соответственно максимальное и минимальное измеренные значения модуля сдвига для всех глубин при сдвиговой деформации n.
На рисунке 12 показаны изменения нормализованных секущих модулей сдвига с глубиной при различных сдвиговых деформациях. Следует отметить, что из-за недостаточности данных, полученных при испытаниях в скважине 1, отдельно суммировались и представлялись в графическом виде только данные по скважинам 2 и 3. Хотя корреляции между модулями для разных глубин видны слабо, что в основном связано с несколькими отдельными точками с большими отклонениями, в целом при всех деформациях можно заметить тенденцию к увеличению модуля сдвига с глубиной. Это также можно отнести и к прерывистым данным, полученным при испытаниях самозабуривающимся прессиометром, так как испытания проводились через каждый метр, а это дает очень высокую плотность расположения точек испытаний. Чтобы улучшить оценки распределения значений модуля сдвига, можно включить также комбинации результатов использования и других методов полевых испытаний, например CPTu.
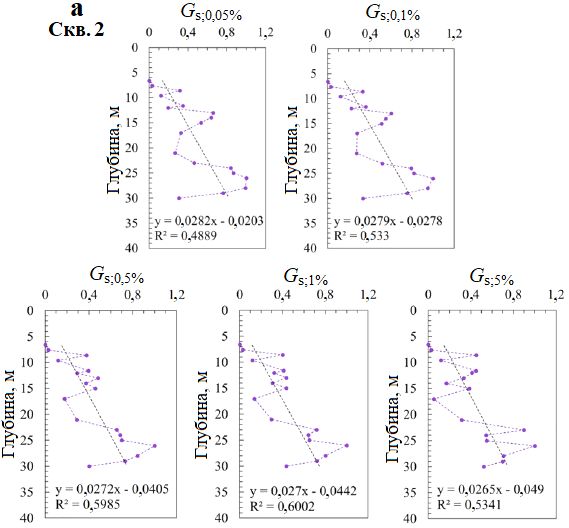
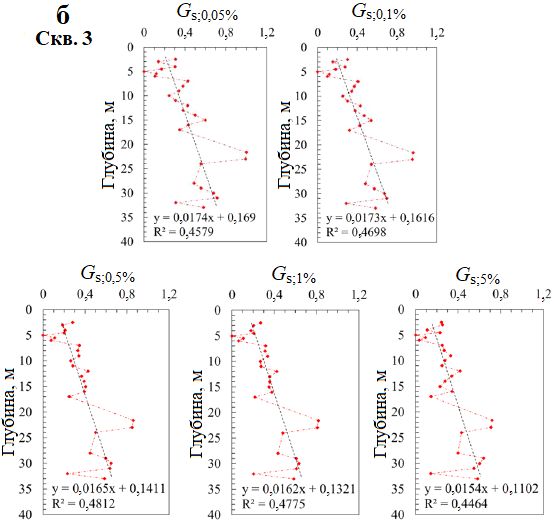
Рис. 12. Распределение по глубине нормализованного модуля сдвига (см. формулу (5)) при сдвиговых деформациях γ, равных 0,05; 0,1; 0,5; 1; 5%, по результатам испытаний самозабуривающимся прессиометром в скважинах 2 (a) и 3 (б)
На основе разрозненных данных был построен ряд линий трендов изменений секущего модуля сдвига, нормализованного по отношению к глубине с помощью формулы (5). Хотя есть небольшое расхождение между графиками для скважин 2 и 3, их объединяет то, что наклон линий трендов уменьшается с ростом сдвиговой деформации. При увеличении деформации от 0,05 до 5% наклон этих линий для скважин 2 и 3 уменьшается соответственно с 0,0282 до 0,0265 и с 0,0174 до 0,0154 (см. пунктирные линии и формулы под ними на рис. 12). Это свидетельствует о том, что при росте сдвиговой деформации тенденция к увеличению модуля сдвига с глубиной замедляется. Когда сдвиговая деформация мала, различия между модулями сдвига с увеличением глубины значительны. С ростом сдвиговой деформации эти различия постепенно уменьшаются. В результате наклон линии тренда изменений секущего модуля сдвига, нормализованного по отношению к глубине с помощью формулы (5), несколько уменьшается с деформацией.
Зависимость между секущими модулями сдвига и числом пластичности
Широко признано, что параметры прочности тесно связаны с физическими параметрами грунта [28, 29, 30, 31]. В настоящей работе была установлена зависимость между модулем сдвига и числом пластичности Ip. Для определения значений Ip были проведены лабораторные испытания различных типов грунтов (см. таблицу 1).
На рисунке 13 показаны корреляции отношения Gs/Gmax с числом пластичности Ip при различных деформациях сдвига. Видны в целом отрицательные зависимости. По мере увеличения числа пластичности отношение Gs/Gmax уменьшается. Это означает, что при одних и тех же деформациях чем выше будет число пластичности, тем ниже получится модуль сдвига, то есть тем больше будет скорость его уменьшения. Отсюда можно сделать простой вывод, что чем больше число пластичности, тем выше скорость ухудшения прочностных свойств дисперсного грунта.
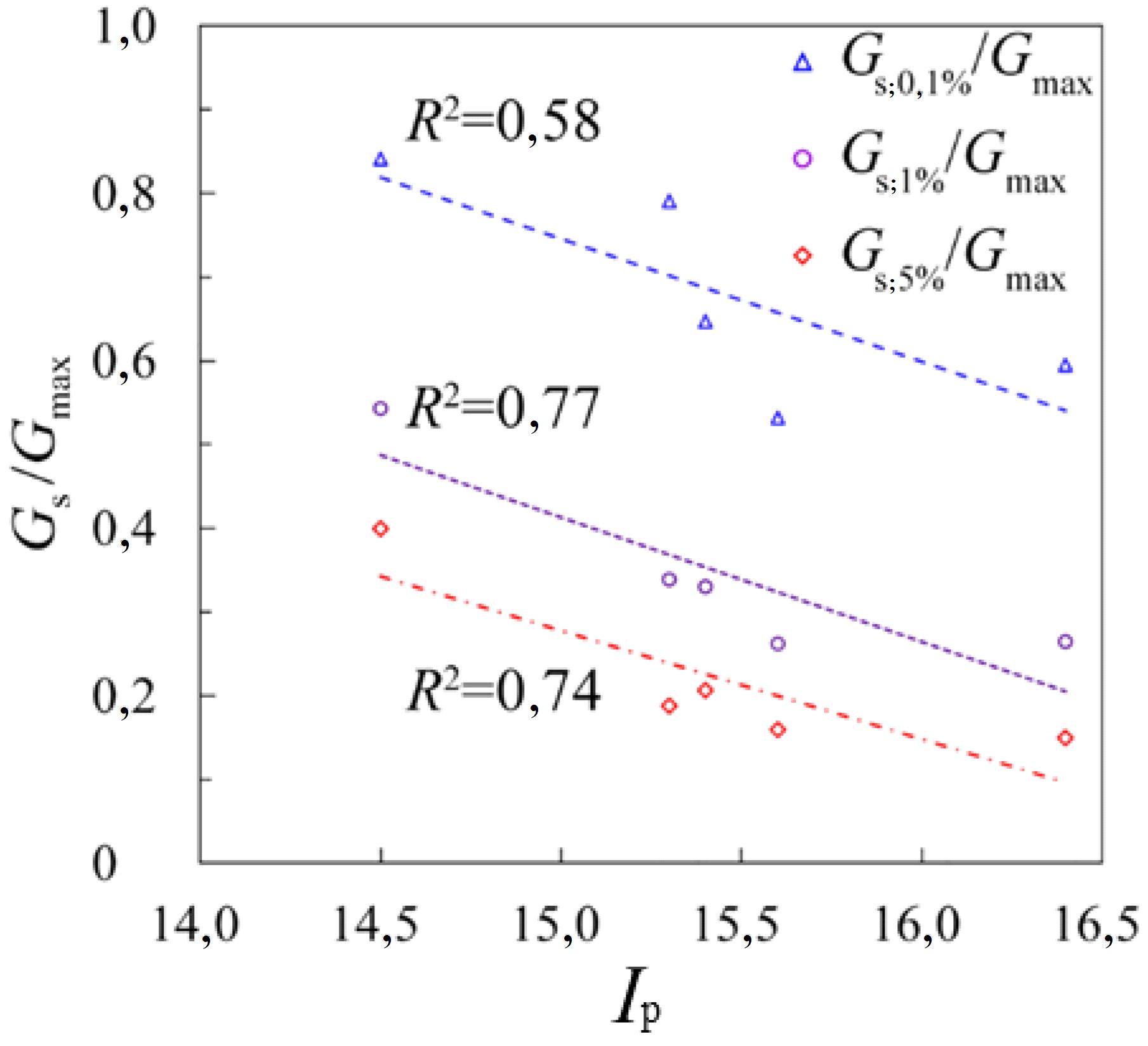
Рис. 13. Корреляции между отношением Gs/Gmax и числом пластичности Ip при различных сдвиговых деформациях
На рисунке 14 представлены зависимости между нормализованным по отношению к глубине модулем сдвига (см. формулу (5)) и числом пластичности при различных сдвиговых деформациях. В целом видно, что эти зависимости являются положительными линейными, при этом по мере увеличения сдвиговой деформации наклон сглаженных графиков уменьшается (составляя 0,472; 0,447; 0,380; 0,350 и 0,278 для относительных деформаций 0,05; 0,1; 0,5; 1 и 5% соответственно).
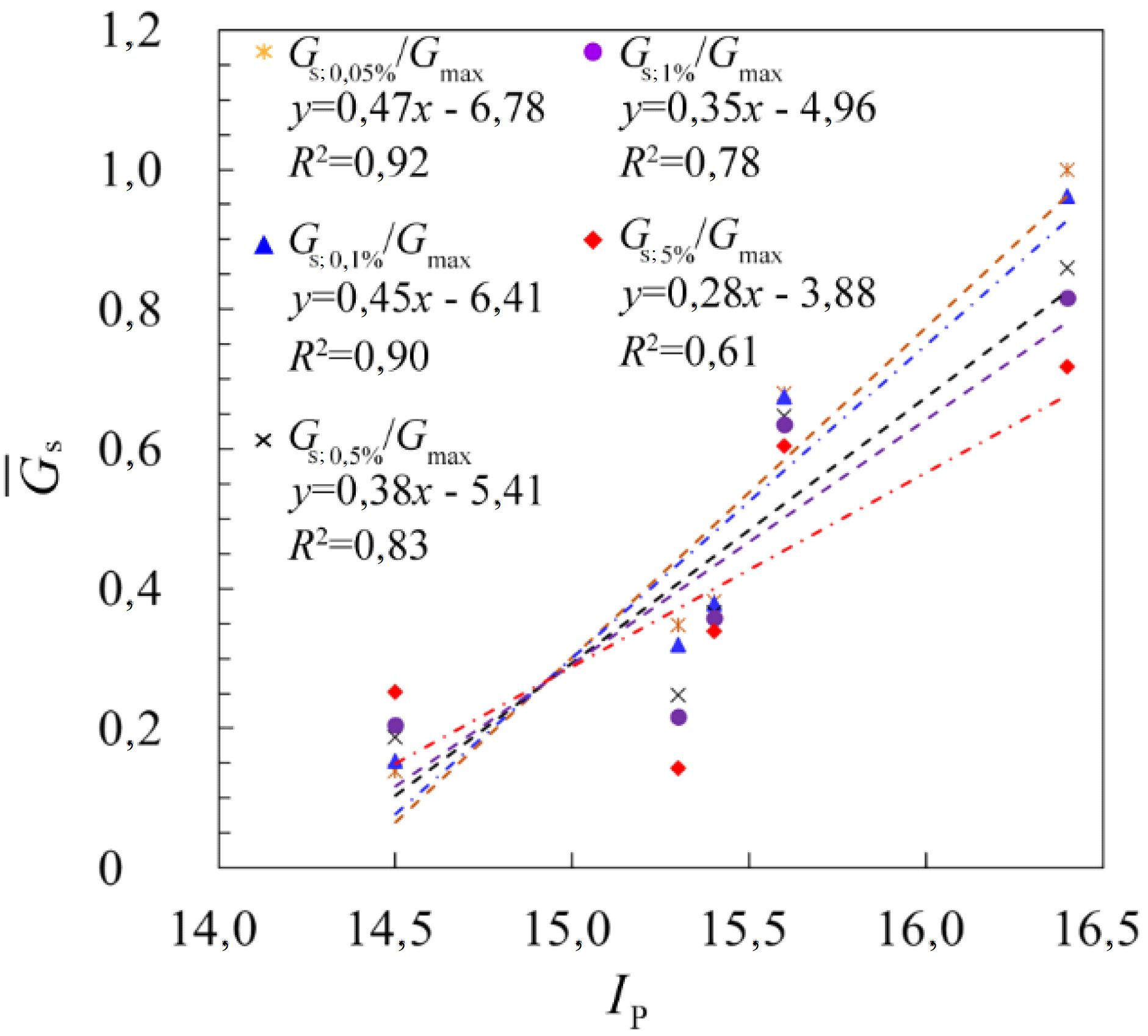
Рис. 14. Корреляции между нормализованным модулем сдвига и числом пластичности при различных сдвиговых деформациях γ, равных 0,05; 0,1; 0,5; 1 и 5%
Из этих графиков можно сделать два вывода.
Во-первых, по мере увеличения числа пластичности нормализованный модуль сдвига (см. формулу (5)), который положительно связан с секущим модулем сдвига Gs, также увеличивается, что указывает на положительную связь между Ip и Gs. Другими словами, чем больше число пластичности Ip, тем выше секущий модуль сдвига Gs.
Во-вторых, с ростом сдвиговой деформации скорость увеличения модуля сдвига по отношению к числу пластичности постепенно уменьшается. Это означает, что влияние числа пластичности на увеличение модуля сдвига уменьшается по мере роста деформации. Следовательно, уменьшение модуля сдвига может быть рассчитано через комбинацию величин деформаций сдвига и изменений числа пластичности. При этом получение количественной оценки того, какой фактор является более важным, может быть исследовано в будущем.
-
В следующей части статьи будут рассмотрены: статистический анализ полученных значений секущего модуля сдвига и недренированной сдвиговой прочности, интервалы корреляции флуктуаций этих параметров, а также будут сделаны общие выводы по всей переведенной работе.
Список литературы, использованной авторами переведенной статьи, можно посмотреть по адресу: mdpi.com/1424-8220/21/18/6026.
ИСТОЧНИК ДЛЯ АДАПТИРОВАННОГО ПЕРЕВОДА
Wang B., Liu K., Wang Y., Jiang Q. Site investigations of the lacustrine clay in Taihu Lake, China, using self-boring pressuremeter test // Sensors (Special Issue “Fault Detection and Data Analysis for Structure and Infrastructure Engineering”). 2021. Vol. 21 (6026). DOI: doi.org/10.3390/s21186026. URL: mdpi.com/1424-8220/21/18/6026.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц