Стратегии строительства тоннеля методом НАМТ в элювиальных грунтах в г. Сан-Паулу (Бразилия). Часть 1

ВВЕДЕНИЕ

Массовый рост городов создает большой спрос на надежную подземную инфраструктуру. Тоннели в городских условиях часто приходится строить на небольшой глубине в слабых грунтах под наземными или заглубленными зданиями или сооружениями. Выемка при этом ограничена минимально допустимыми деформациями грунта. Все это усложняет проектирование и строительство.

Новый австрийский метод тоннелестроения (НАМТ) (от англ. New Austrian Tunneling Method – NATM) широко и успешно применяется для проходки неглубоких тоннелей в городских районах со сложными условиями. Например, этот метод в комплексе с укреплением (первичной обделкой) внутренних поверхностей тоннелей с помощью набрызг-бетона, или торкрет-бетона (от англ. Sprayed Concrete Lining – SCL), то есть методом торкретирования, широко используется в крупных городах тропических регионов. К сожалению, к настоящему моменту проведено мало исследований для оценки деформаций в элювиальных грунтах, распространенных в тропиках.

В данной статье собрана информация по строительству тоннеля «Параисо» системы метро города Сан-Паулу (Бразилия). В программном комплексе midas GTS NX (от компании MIDAS IT), предназначенном для решения геотехнических задач любого уровня, был выполнен трехмерный анализ с тщательным моделированием всей последовательности строительства рассматриваемого тоннеля.

Данные по неглубокому тоннелю «Параисо», проложенному в глинистых грунтах с широким диапазоном прочности и деформируемости, были хорошо задокументированы бразильскими специалистами в ряде исследований (список тех из них, которые использовались для написания переведенной статьи, приведен в конце). Результаты, полученные авторами данной работы, предоставили качественную и количественную информацию о деформировании грунта, вызванном проходкой тоннеля методом НАМТ в пористых грунтах коры выветривания, и могут помочь проектировщикам и подрядчикам в выборе оптимальных методов создания подобных сооружений в похожих условиях для минимизации деформаций грунта.

Ключевые преимущества метода НАМТ включают относительно простое исполнение, большую гибкость на этапе строительства и снижение затрат на реализацию проекта.

Процесс создания тоннелей с использованием этого метода может оказывать значительное влияние на деформации вмещающих их грунтовых массивов. Он основан на последовательной выемке грунта в зоне забоя по частям и в соответствующем последовательном выполнении обделки (почти сразу после выемки) для уменьшения деформаций. В городских районах все это обычно производится небольшими шагами. Как правило, выемка начинается у свода, а затем последовательно (например, по ступеням или уступам) продвигается к обратному своду. Первичная обделка тоннеля обычно производится торкрет-бетоном в сочетании с арматурой из фибры или сварной проволочной сетки, стальными ребрами жесткости (арками), анкерными болтами и пр.

Во время строительства тоннеля выполняется мониторинг деформаций его обделки и вмещающего его грунтового массива, а полученные результаты измерений сравниваются с показателями деформаций, спрогнозированными при проектировании. Поэтому выемку грунта и создание обделки можно оптимизировать по мере появления новых данных прямо во время строительства.

В тропических регионах распространены латеритные (красные) элювиальные грунты. Они могут быть сильно выветрелыми и обильно выщелоченными, поэтому коэффициент их пористости может оказаться высоким, а структура – неустойчивой и слабосвязной. Прокладка тоннелей в таких грунтах может приводить к сильным деформациям грунтовых массивов, что, в свою очередь, оказывает воздействие на близлежащие наземные и заглубленные здания и сооружения.

Например, Ортигао и др. ( Ortigao et al., 1996) и Маркес ( Marques, 2006) сообщали, что во время выемки нескольких километров грунтов для строительства участка метро в городе Бразилия в элювиальных пористых грунтах произошли большие деформации и осадки дневной поверхности вплоть до 500 мм. Они также отмечали необычное поведение вмещающих тоннель грунтов: вертикальные смещения уменьшались с глубиной (осадки на поверхности грунта были больше, чем у свода тоннеля), что противоречило ожидаемому поведению. Соотношение осадок на поверхности и у свода тоннеля находилось в диапазоне 1,2–1,3. Такое поведение, например, Ortigao и Маседо (Ortigao, Macedo, 1993) посчитали связанным со склонностью выветрелого пористого грунта к сжатию (к «схлопыванию»).

Большие деформации грунта наблюдались и во время строительства в г. Сан-Паулу тоннеля «Параисо», проходка которого велась в элювиальном пористом грунте. Азеведо и др. (Azevedo et al., 2002) выполнили для этого тоннеля двумерный анализ методом конечных элементов (МКЭ) при помощи усовершенствованной комплексной геомеханической модели Ладе (Lade), чтобы описать поведение элювиального пористого грунта, вмещающего тоннель. Параметры этой модели были откалиброваны по результатам лабораторных испытаний ненарушенных образцов, которые провел Паррейра (Parreira, 1991). Азеведо и др. (Azevedo et al., 2002) отметили, что деформации грунта вокруг тоннеля лучше прогнозируются при помощи модели упрочняющегося грунта (Hardening Soil model), а не модели Мора – Кулона (Mohr-Coulomb model).

Альмейда-э-Соуза и др. (Almeida e Souza et al., 2011) отметили, что мульда оседания для этого тоннеля не была хорошо отражена эмпирической кривой Гаусса, тогда как кривая «текучесть – плотность» предложенная в работах Селестино и Руиса (Celestino, Ruiz, 1998) и Селестино и др.(Celestino et al., 2000), точно соответствует результатам реальных измерений.

Альмейда-э-Соуза и др. (Almeida e Souza et al., 2011) провели трехмерный конечноэлементный анализ для рассматриваемого тоннеля с использованием модели грунта Ладе с параметрами, которые откалибровали Паррейра (Parreira, 1991) и Азеведо и др. (Azevedo et al., 2002), и  получили убедительное совпадение численных результатов с данными реальных измерений. Таким образом, было показано, что для правильного воспроизведения деформаций вокруг тоннеля следует использовать нелинейную геомеханическую модель. Альмейда-э-Соуза и др. (Almeida e Souza et al., 2011) также показали, что при 2D-анализе невозможно зафиксировать сложные траектории напряжений вблизи забоя. По данным Кантиени и Анагносту (Cantieni, Anagnostou, 2009), радиальные напряжения в грунте по периметру тоннеля увеличиваются перед забоем, уменьшаются до нуля на незакрепленном участке тоннеля и далее увеличиваются за обделкой тоннеля. Кроме того, как доказали Энджи и Ли (Ng, Lee, 2005), вблизи забоя мобилизуются осевые (продольные) напряжения сдвига, которые могут оставаться мобилизованными (то есть не уменьшаются до нуля) далеко позади забоя. Как показал Эберхардт (Eberhardt, 2001), мобилизация осевых (продольных) напряжений сдвига вблизи забоя, обусловленная свойствами грунта, приводит к повороту основных направлений напряжений. Как отметил Моллер (Moller, 2006), попытки сопоставить методики 2D- и 3D-анализа показали, что так называемый коэффициент снижения напряжений (stress relief factor) существенно меняется в зависимости от рассматриваемых характеристик (то есть осадок на поверхности, на глубине или внутренних усилий в обделке) и от последовательности этапов строительства тоннеля.

Несмотря на большой спрос на тоннели мелкого заложения в пористых грунтах коры выветривания, подверженных сильным деформациям, на данный момент проведено недостаточное количество исследований, посвященных изучению деформаций грунта, вызванных созданием тоннелей.

Aвторами данной статьи [1] был выполнен трехмерный конечноэлементный анализ тоннеля «Параисо» с использованием модели упрочняющегося грунта. Было получено убедительное совпадение численных результатов с данными полевых исследований. Затем эта модель использовалась для изучения влияния разных стратегий строительства на деформации грунта и устойчивость забоя. Несмотря на то что количественные результаты зависят от конкретных случаев, качественные выводы (влияние выемки грунта в забое по частям или одновременно, длина незакрепленного участка, жесткость обделки и т.д.) являются общими и могут быть экстраполированы для разных сценариев.

ОБЩАЯ ИНФОРМАЦИЯ О ПРОЕКТЕ

Строительство тоннеля «Параисо» было завершено в 1991 году. Подробная информация об этом тоннеле представлена в работе Паррейры (Parreira, 1991).

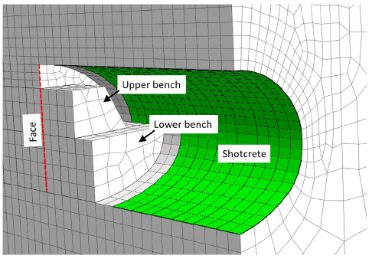
На рисунке 1 показаны поперечное сечение тоннеля и последовательность выемки грунта. Поперечное сечение имело эллипсоидальную форму (ширину 11,6 м и высоту 8,5 м). Выемка выполнялась в последовательности «1 – 2 – 3» от свода по двум уступам к обратному своду (см. рис. 1). Выемка проводилась шагами по 1,6 м. Для повышения устойчивости забоя сохранялось два уступа. Сразу после выемки в зоне свода устанавливалось два комплекта стальных ребер, расположенных с шагом 0,8 м, и на внутреннюю поверхность тоннеля наносили слой набрызг-бетона толщиной 0,2 м. Выемку в зоне обратного свода проводили в 4,8 м от верхней части забоя, также продвигаясь шагами по 1,6 м. На обратный свод тоннеля также наносили слой набрызг-бетона толщиной 0,2 м, но армированного проволочной сеткой. Позже создавали вторичную обделку тоннеля из монолитного бетона (железобетона) толщиной 0,15 м.

Рис. 1. Поперечное (а) и продольное (б) сечение тоннеля «Параисо» в зоне забоя. Выемка выполнялась в последовательности «1 – 2 – 3» от свода по двум уступам к обратному своду [1]

Геотехническое исследование рассматриваемой территории выявило наличие (сверху вниз) тонкого слоя техногенного грунта, оставшегося от полигона твердых отходов, слоя элювиальной красной пористой глины, слоя элювиальной полутвердой пестроцветной глины и слоя очень плотной супеси. На границе между красной и пестроцветной глинами был обнаружен водоносный горизонт. Красная глина оказалась неводонасыщеной, и при возведении тоннеля водопритока из нее не наблюдалось. По этой причине при выемке из этого слоя понижение уровня грунтовых вод не проводилось.

Для рассмотренного поперечного сечения слой красной глины имел толщину 12 м, слой пестроцветной глины – 10,6 м.

Описанные грунтовые условия были такими же, как и принятые для анализа в работах Азеведо и др. (Azevedo et al., 2002) и Альмейда-э-Соуза и др. (Almeida e Souza et al., 2011). Верх свода тоннеля располагался на глубине 7,6 м от дневной поверхности. Выемка в зоне свода велась в красной глине, а в зоне обратного свода – в пестроцветной глине.

Как уже отмечалось, во время земляных работ велся мониторинг деформаций обделки тоннеля и вмещающего его грунтового массива. Осадки дневной поверхности грунта измерялись с использованием нивелирных марок. Вертикальные смещения над сводом тоннеля измеряли с помощью вертикальных экстензометров, а горизонтальные смещения вблизи пят свода тоннеля (его боков) – при помощи инклинометра. Деформации в первичной обделке из торкрет-бетона измеряли на своде и по периметру тоннеля. На рисунке 2 схематично показаны инженерно-геологические условия и расположение контрольно-измерительной аппаратуры для мониторинга поведения обделки и вмещающих тоннель грунтов.

Рис. 2. Инженерно-геологические условия и контрольно-измерительная аппаратура для мониторинга поведения тоннеля и вмещающего его грунтового массива [1]

КАЛИБРОВКА МОДЕЛИ ПОВЕДЕНИЯ ЭЛЮВИАЛЬНОЙ КРАСНОЙ ПОРИСТОЙ ГЛИНЫ

Инженерно-геологические свойства элювиальной красной пористой глины широко изучены. Этот грунт классифицируется как латеритный. Его характеризуют сильная степень выветрелости и выщелачивания, высокий коэффициент пористости и нестабильный состав. В 1990 году была обнаружена зависимость поведения таких грунтов от их состава (Leroueil, Vaughan, 1990), а годом позже Паррейра (Parreira, 1991) провел комплексные лабораторные испытания ненарушенных образцов этой глины, взятых в местах выемки с глубины 3,5 и 6,5 м. В таблице 1 приведены ее характеристики, определенные по результатам указанных испытаний, а также показатели свойств элювиальной пористой глины Сан-Паулу, взятые из работы Массада и др. (Massad et al., 1992). Свойства образцов с глубины 3,5 и 6,5 м оказались схожими и попали в диапазон ожидаемых значений для элювиальной красной пористой глины Сан-Паулу. Следует обратить внимание на то, что эти грунты не являются водонасыщенными. Как отмечает Паррейра (Parreira, 1991), если содержание воды увеличивается, структура такого грунта разрушается, приводя к большим объемным деформациям.

Таблица 1. Показатели свойств элювиальной красной пористой глины Сан-Паулу [1]

На рисунке 3 представлены зависимости максимальных напряжений сдвига q = (σ₁ – σ₃)/2 и относительных объемных деформаций в зависимости от относительной осевой деформации, полученные по данным трехосных испытаний при нагружении (см. рис. 3, а) и разгрузке (см. рис. 3, б). Также показаны результаты численного моделирования трехосных испытаний – откалиброванные кривые на основе модели упрочняющегося грунта (Schanz et al., 1999). Последние, как видно из рисунка 3, неплохо соответствуют экспериментальным данным.

При сжимающем нагружении во время трехосных испытаний (см. рис. 3, а) грунт деформируется по гиперболической кривой приблизительно при 20%-ной осевой деформации. Примечательно, что начальная жесткость элювиальной красной пористой глины уменьшается по мере увеличения всестороннего давления с 25 до 98 кПа (Parreira, 1991). Такое поведение было бы неожиданным для обычных грунтов, но в данном случае это посчитали связанным со структурой грунта. Модель упрочняющегося грунта смогла неплохо отразить экспериментальные объемные деформации, поскольку они слабо зависели от всестороннего сжатия. Объемные деформации при трехосных испытаниях оказались значительными (до 12%), что было ожидаемо для элювиальных пористых грунтов из-за высокого коэффициента пористости и нестабильной структуры. Использованная комплексная геомеханическая модель грунта хорошо соответствовала объемным деформациям вплоть до осевой деформации около 10%, после чего она стала слегка занижать значения объемных деформаций.

Измерения на стадии разгрузки во время трехосных испытаний (см. рис. 3, б) показали начальное квазилинейное увеличение максимального напряжения сдвига с ростом осевой деформации до 0,2%. После этого максимальное напряжение сдвига увеличивалось совсем немного с ростом осевой деформации. Модель упрочняющегося грунта смогла воспроизвести это поведение. Но в отношении объемных деформаций модель спрогнозировала гораздо меньшее их увеличение при росте осевых деформаций, чем показали реальные испытания.

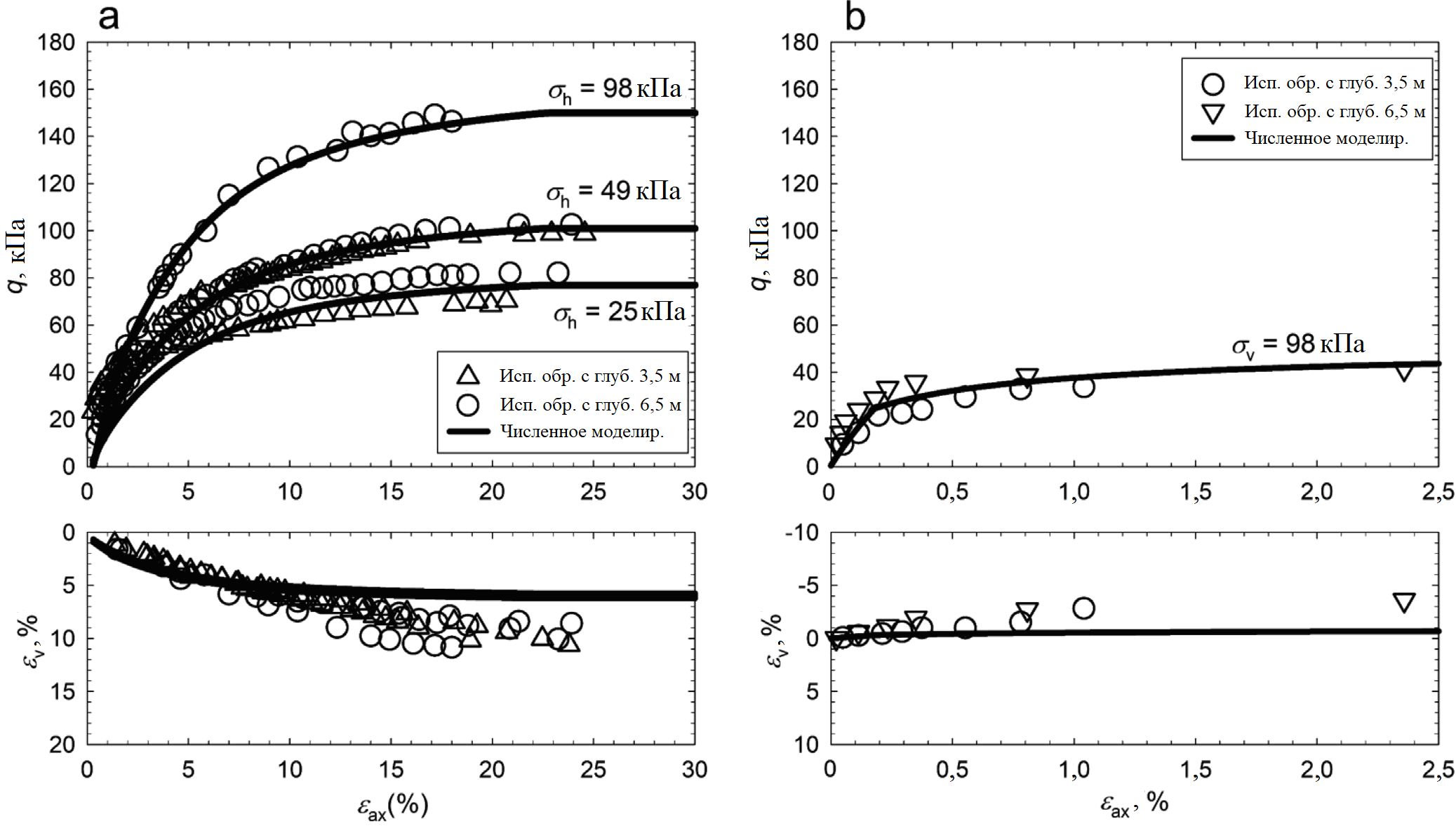
Рис. 3. Экспериментальные данные и результаты численного моделирования трехосных испытаний: а – трехосное сжимающее нагружение при всестороннем давлении 25, 49 и 98 кПа; б – разгрузка на ступени вертикального напряжения 98 кПа. Буквенные обозначения: σ_h – горизонтальное напряжение, σ_v – вертикальное напряжение, ε_v – относительная объемная деформация; ε_ax – относительная осевая деформация [1]

Воан и Кван (Vaughan, Kwan, 1984) показали, что по мере выветривания и выщелачивания природные горизонтальные напряжения в массиве грунтов уменьшаются. Они заметили, что, когда жесткость выветрелого грунта снизилась до 1% от первоначальной, естественное горизонтальное напряжение приблизилось к следующему пределу:

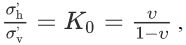
где σ'_h – эффективное горизонтальное напряжение; σ'_v – эффективное вертикальное напряжение; K₀ – коэффициент бокового (горизонтального) давления грунта в состоянии покоя; ν – коэффициент Пуассона.

То же верно и для выветрелого пористого грунта. Согласно данным исследования Воана и Квана (Vaughan, Kwan, 1984) традиционные лабораторные испытания для определения K₀ разрушили структуру грунта, поэтому возникла тенденция к завышению величин K₀. Ортигао и др. (Ortigao et al., 1995) выполнили измерения этого коэффициента in situ при помощи прессиометра Менара (в публикациях на русском языке часто пишут «Менарда», но это неправильно для этой фамилии французского происхождения. – Ред.) и получили значения K₀, примерно равные 0,5.

В таблице 2 представлены откалиброванные параметры для модели упрочняющегося грунта. При определении наиболее подходящих значений параметров учитывались численные результаты трехмерного конечноэлементного моделирования тоннеля Параисо и вмещающего его грунтового массива. Другими словами, в таблице 2 представлены наилучшие прогнозы для выбранных лабораторных трехосных испытаний и для данных полевых исследований.

Таблица 2. Откалиброванные параметры для модели упрочняющегося грунта, использованные при моделировании поведения элювиальной красной пористой глины Сан-Паулу [1]

(Буквенные обозначения параметров в таблице 2: E_50,ref – эталонный модуль деформации (жесткость), соответствующий эталонному всестороннему давлению p_ref, равному бытовому давлению (наименьшему главному напряжению в условиях естественного залегания), кПа; E_oed,ref – эталонный компрессионный (одометрический) модуль деформации, соответствующий эталонному всестороннему давлению p_ref, кПа (эталонная жесткость для первичной нагрузки в одометре); E_ur,ref – эталонный модуль разгрузки и повторного нагружения при эталонном всестороннем давлении p_ref, кПа (эталонная жесткость при разгрузке/повторном нагружении); R_f – коэффициент разрушения (критерий разрушения – соотношение q_f /q_a, характеризующее интенсивность разрушения, которое должно быть меньше единицы, где: q_f  – предельное девиаторное напряжение, являющееся пределом деформирования, рассчитанное по закону Кулона, кПа; q_a – асимптотический уровень прочности, к которому стремится зависимость между напряжениями и деформациями, кПа); n – показатель степени в степенном законе зависимости жесткости от уровня напряжений, задающий кривизну этой зависимости; ψ – угол внутреннего трения; K_0,NC – коэффициент K₀, для нормальной консолидации; ψ – угол дилатансии, c – удельное сцепление, γ_n – удельный вес в условиях естественного залегания (природный); OCR – коэффициент переуплотнения. – Ред.).

В таблице 3 приведены показатели свойств грунта, принятые для элювиальной пестроцветной глины, подстилающей элювиальную красную пористую глину (см. рис. 2). Те же показатели использовали в своей работе Альмейда-э-Соуза и др. (Almeida e Souza et al., 2011). Для описания поведения пестроцветной глины была принята модель Мора – Кулона, поскольку деформации в слое грунта были небольшими.

Таблица 3. Параметры модели Мора – Кулона, использованные при моделировании поведения элювиальной пестроцветной глины [1]

ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ТОННЕЛЯ ПАРАИСО И ВМЕЩАЮЩЕГО ЕГО ГРУНТОВОГО МАССИВА

Для анализа поведения тоннеля Параисо и вмещающего его грунтового массива было выполнено трехмерное конечноэлементное моделирование в программном комплексе midas GTS NX, разработанном южнокорейской компанией MIDAS IT (MIDAS, 2019). Сетка конечных элементов была построена с использованием гексаэдрических элементов второго порядка и была достаточно мелкой для обеспечения точности численных результатов (Vitali et al., 2018; Vitali et al., 2021).

Размеры модели были выбраны таким образом, чтобы избежать влияния на результаты со стороны ее границ. Поскольку выемка грунта проводилась симметрично относительно вертикальной оси тоннеля, рассматривалась лишь половина тоннеля (рис. 4). Нижняя граница модели проходила между слоями пестроцветной глины и очень плотной супеси (на 6,5 м ниже обратного свода). Взвешивающие гидростатические воздействия на тоннель были пренебрежимо малыми, потому что нижняя граница сетки располагалось близко к тоннелю. Нижняя и боковые границы были зафиксированы так, чтобы не было их смещений в нормальных к ним направлениях. Горизонтальные смещения поверхности грунта были ограничены, чтобы учесть эффект дорожного покрытия, как рекомендовали Азеведо и др. (Azevedo et al., 2002) и Альмейда-э-Соуза и др. (Almeida e Sousa et al., 2011).

Рис. 4. Сетка конечных элементов и размеры модели в программе midas GTS NX [1]

Элювиальная красная пористая глина оставалась в неводонасыщенном состоянии, в то время как элювиальная пестроцветная глина была полутвердой, трещиноватой и сильно переуплотненной. Поэтому для обоих этих слоев ожидалось дренированное поведение и при конечноэлементном анализе рассматривались дренированные условия. На уровне обратного свода тоннеля был обнаружен водоносный горизонт, но в ходе строительства тоннеля Параисо ни разу не сообщалось о водопритоке, а деформации элювиальной пестроцветной глины были маленькими. Таким образом, влияние уровня грунтовых вод в данном конкретном случае не имело значения и поэтому не учитывалось при трехмерном конечноэлементном анализе.

На рисунке 5 представлен поперечный разрез рассматриваемой модели. Сетка была сделана более мелкой над сводом тоннеля и вблизи него по бокам, где деформации грунта были больше. При трехмерном анализе методом конечных элементов учитывалась описанная ранее последовательность создания тоннеля, как показано на рисунке 6.

Рис. 5. Поперечный разрез конечноэлементной модели тоннеля Параисо и вмещающего его грунтового массива в программе midas GTS NX [1]

Рис. 6. Численное моделирование последовательности выемки грунта в забое тоннеля Параисо [1]

Длина шагов выемки грунта составляла 1,6 м. А длина гексаэдрических элементов второго порядка была равна 0,8 м. Поэтому продольная густота сетки конечных элементов была достаточной для получения точных результатов (Vitali et al., 2018).

Работа модели предусматривала 37 этапов производства работ. На первом этапе было сгенерировано поле геостатических напряжений, в котором коэффициент бокового давления грунта в состоянии покоя K₀ был равен 0,5 для элювиальной красной пористой глины и 0,84 для элювиальной пестроцветной глины. На последующих этапах моделировались процессы выемки грунта и создания обделки (соответственно путем деактивации элементов, соответствующих определенной последовательности выемок, и активации элементов, представляющих обделку тоннеля). Первичная обделка тоннеля из торкрет-бетона и стальных ребер жесткости была представлена оболочечными конечными элементами толщиной 0,2 м с линейно-упругим поведением. Проскальзывание между грунтом и обделкой не допускалось. Эта обделка имела следующие показатели свойств: модуль Юнга E = 5 ГПа; коэффициент Пуассона ν = 0,2. Величины жесткости, принятые для обделки, были довольно малы по сравнению с типичными ее значениями. Они были приняты для моделирования торкрет-бетона на ранней стадии твердения и уменьшенной конечной жесткости из-за нагрузки на торкрет-бетон на ранней стадии твердения (Golser, 2001).

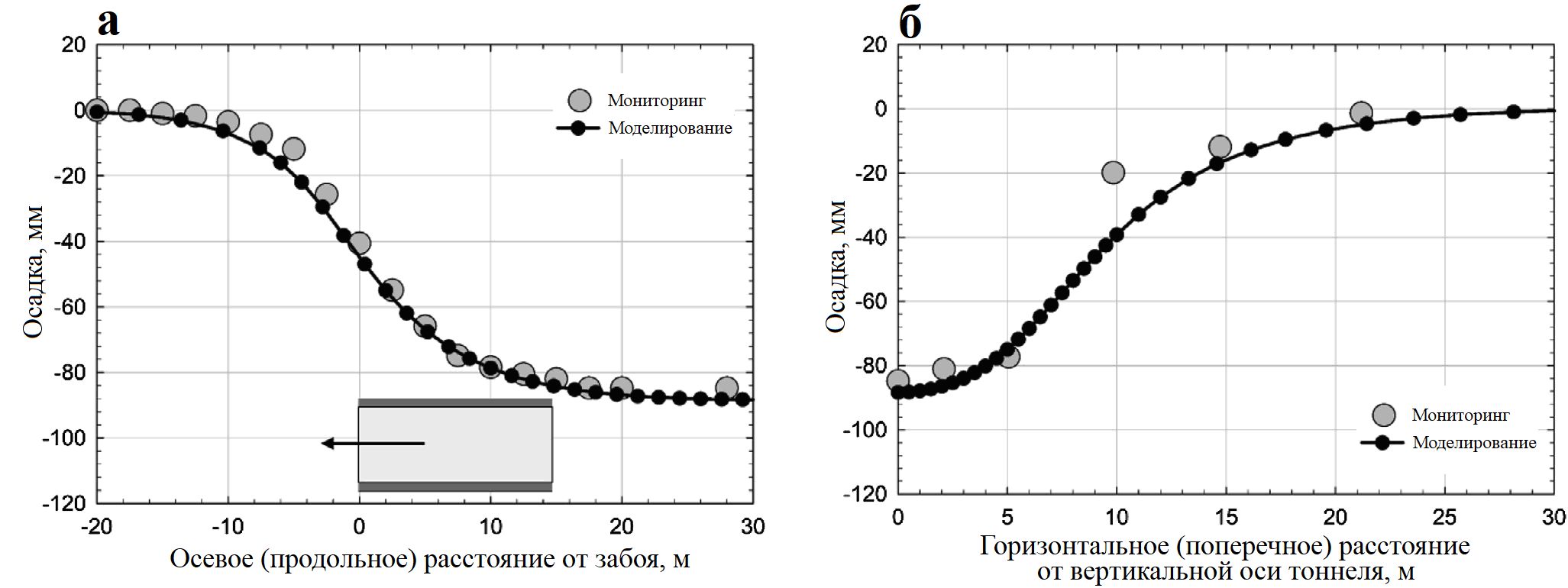
На рисунке 7 показаны осадки дневной поверхности в зависимости от продольного расстояния от забоя тоннеля (см. рис. 7, а) и от поперечного горизонтального расстояния от вертикальной оси тоннеля (см. рис. 7, б), то есть продольный профиль и мульда осадок соответственно, полученные при мониторинге и при численном моделировании. Численные результаты и измеренные деформации грунта показали убедительное соответствие друг другу.

Продольный профиль осадок (см. рис. 7, а) имеет сигмоидальную форму. Осадки начинают увеличиваться в 20 м перед забоем (примерно на расстоянии двух диаметров тоннеля) и стабилизируются примерно в 20 м позади забоя. Измеренная осадка непосредственно над забоем тоннеля составила 41 мм, а по результатам численного моделирования – 45 мм. Далеко позади забоя измеренная осадка над сводом составила 85 мм, а модельная – 89 мм.

Как видно из рисунка 7, б, модельные осадки были близки к результатам измерений, за исключением участка примерно в 10 м вбок от вертикальной оси тоннеля, где модельная осадка оказалась равной 39 мм, а измеренная – 20 мм. Точная причина этого несоответствия неизвестна. Появлению такой разницы может способствовать ряд причин: неоднородность грунта, сложности в месте измерения и, безусловно, численные ошибки. Тем не менее эта модель достаточно точно спрогнозировала деформации грунта в других точках и размер мульды оседания, что свидетельствует о ее достоверности.

Рис. 7. Осадки поверхности грунта в зависимости от: а – осевого (продольного) расстояния от забоя тоннеля; б – горизонтального (поперечного) расстояния от вертикальной оси тоннеля

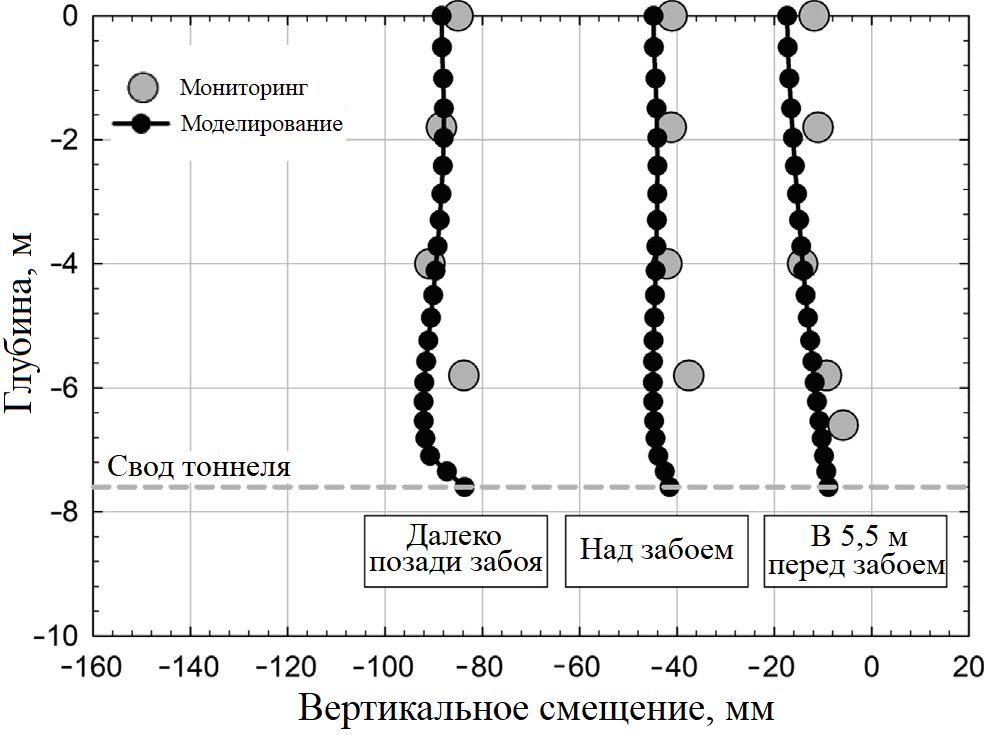
На рисунке 8 показаны вертикальные смещения грунта над сводом тоннеля на разной глубине и на разных расстояниях от забоя (расположение вертикального экстензометра показано на рисунке 2). Результаты численного моделирования и данные мониторинга и здесь убедительно совпали. Вертикальные смещения оказались практически одинаковыми на разной глубине. Далеко позади забоя численная модель показала резкое уменьшение вертикальных смещений вблизи свода, что связано с трехмерными эффектами забоя. Подобное поведение отличалось от ожидаемого (Mair et al., 1993), при котором вертикальные смещения над сводом тоннеля увеличивались с глубиной. Возможно, это является результатом больших объемных деформаций, возникающих из-за повышенной сжимаемости элювиальных пористых грунтов (Ortigao, Macedo, 1993; Ortigгo et al., 1996; Marques, 2006; Nakai et al., 1997).

Рис 8. Вертикальные смещения грунта над сводом тоннеля на разной глубине от дневной поверхности на разных расстояниях от забоя

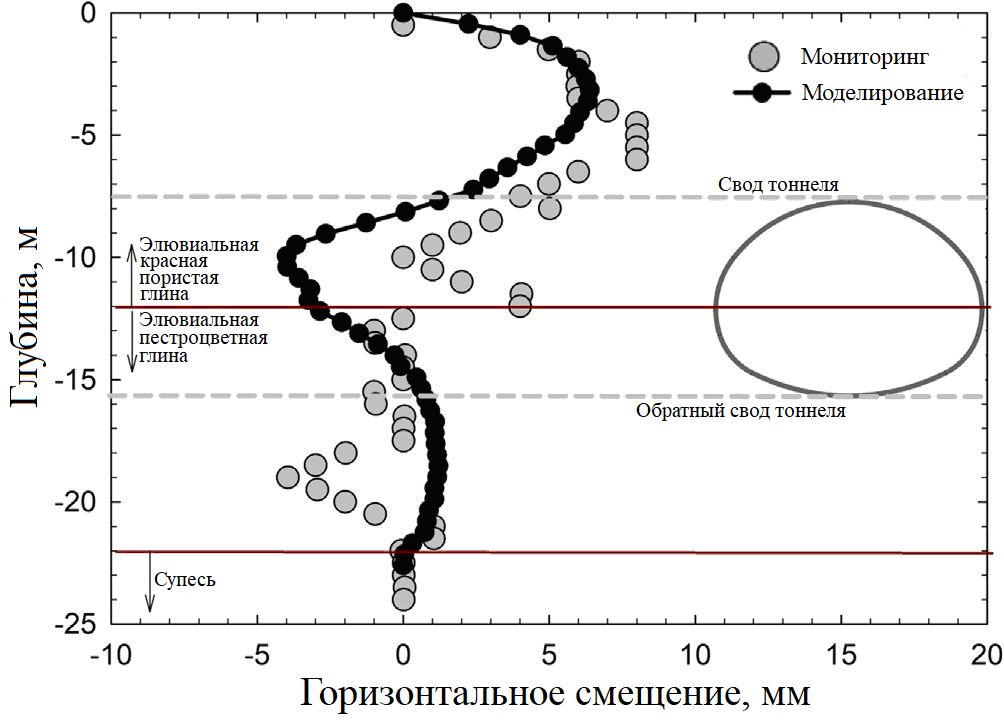
На рисунке 9 изображены горизонтальные смещения вблизи боков (пят свода) тоннеля (расположение инклинометра представлено на рисунке 2). На дневной поверхности они оказались нулевыми, так как их сдерживала мостовая. Горизонтальные смещения увеличивались до достижения глубины около 6 м от поверхности (1,6 м над сводом тоннеля), а затем снижались до нуля на глубине 10 м. Затем они снова увеличивались, достигнув пика при переходе от элювиальной красной пористой глины к элювиальной пестроцветной глине. Ниже этой границы, на глубине 12 м, наблюдались очень незначительные смещения пестроцветной глины вплоть до глубины 18 м. На глубине от 18 до 20 м (на 2–4 м ниже обратного свода тоннеля) инклинометр зарегистрировал неожиданное увеличение горизонтальных смещений. На еще большей глубине деформации грунта, представляющего собой полутвердую глину, должны быть малы.

Относительно большие смещения, полученные при измерениях инклинометром, могут быть вызваны рядом причин: ошибками в измерениях или неоднородностью грунта в определенных местах, где он может быть более слабым. Численные результаты показали увеличение горизонтальных смещений до глубины 5 м, что совпало с данными мониторинга. Ниже этого уровня модельные горизонтальные смещения снизились, что также совпало с результатами измерений, однако первые превышали вторые. В пестроцветной глине модельные горизонтальные смещения оказались небольшими, как и ожидалось для этого полутвердого грунта.

Рис. 9. Горизонтальные смещения вблизи боков (пят свода) тоннеля

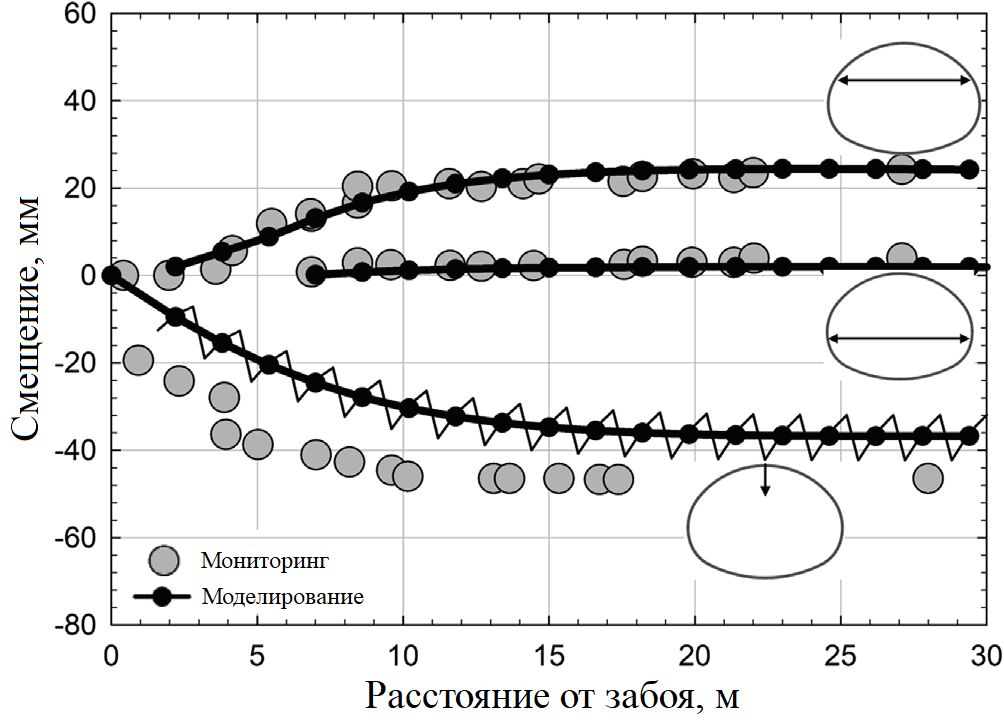
На рисунке 10 показаны вертикальные смещения первичной обделки свода (торкрет-бетона со стальной арматурой) и относительные горизонтальные смещения боков тоннеля в зависимости от осевого (продольного) расстояния от забоя тоннеля. Смещения увеличивались с расстоянием от забоя до приблизительно 10 м позади него (примерно на один диаметр тоннеля), где деформации обделки стали постоянными. Большие деформации (вплоть до 46 мм) наблюдались в своде тоннеля, в то время как в обратном своде они были пренебрежимо малыми. Смещения в двух местах по периметру тоннеля, рассчитанные с помощью численной модели, хорошо совпали с измеренными.

Изменения модельных вертикальных смещений свода имели пилообразную форму с колебаниями в диапазоне 33–43 мм. Среднее модельное смещение составило 38 мм, что на 8 мм ниже измеренных деформаций. Пилообразная форма проявилась и в других численных моделях тоннелей (Moller, 2006; Vitali et al., 2018) и была связана с резкой разницей в жесткости обделки и грунта на конце обделки рядом с забоем. Кроме того, период этого пилообразного графика соответствовал длине шага выемки/креплении грунта в численной модели.

Рис. 10. Горизонтальные смещения первичной обделки (торкрет-бетона)

На рисунке 11 показаны траектории напряжений для точек в грунте по периметру на расстоянии 0,25 м от его контура (что позволило избежать сингулярности в остром углу забоя в месте, где забой пересекал периметр).

Были исследованы три точки: рядом с верхней частью свода, рядом с пятой свода и в точке у периметра тоннеля между ними (см. рис. 11). Все эти точки находились в элювиальной красной пористой глине, в которой и происходило большинство деформаций грунта. Перед забоем и среднее, и максимальное напряжение сдвига увеличивалось по направлению к выемке. В грунте у незакрепленного участка происходила разгрузка (снижение и среднего, и максимального напряжения сдвига), а за обделкой напряжения с увеличением расстояния от забоя увеличивались до тех пор, пока не становились постоянными далеко позади забоя.

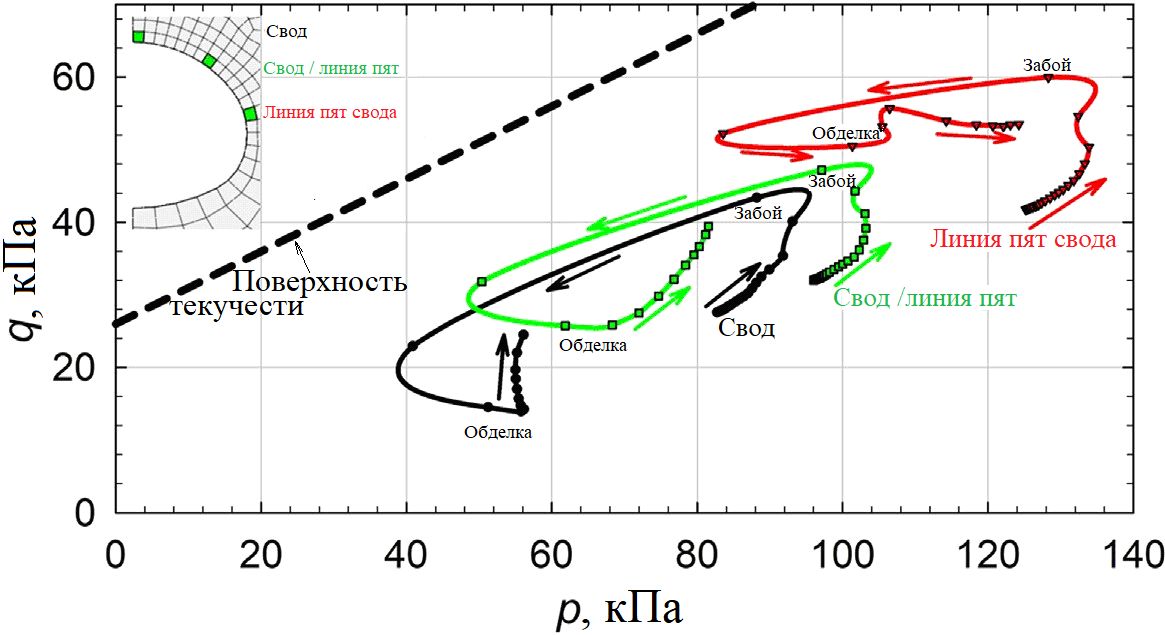
Рис. 11. Траектории напряжений для точек в грунте по периметру тоннеля [1]. Обозначения: q – максимальное напряжение сдвига, q = (σ₁ – σ₃)/2; p – среднее напряжение, p = (σ₁+σ₃)/2 (Lambe and Whitman, 1969)

На рисунке 12 представлены напряжения в грунте у свода тоннеля по его периметру. Напряжения начали изменяться на расстоянии около 10 м перед забоем. Радиальное напряжение в грунте (σ_rr) увеличилось перед забоем, снизилось до нуля на незакрепленном участке и далее увеличилось за обделкой, пока не достигло постоянной величины. Тангенциальное (σ_θθ) и осевое (σ_zz) напряжения совсем немного выросли перед забоем, уменьшились на незакрепленном участке и далее увеличились за обделкой. Осевое напряжение сдвига (τ_rz) было нулевым далеко перед забоем и увеличивалось по мере приближения к забою. У забоя значение τ_rz было максимальным, а затем уменьшалось до тех пор, пока не достигало постоянной величины далеко позади забоя.

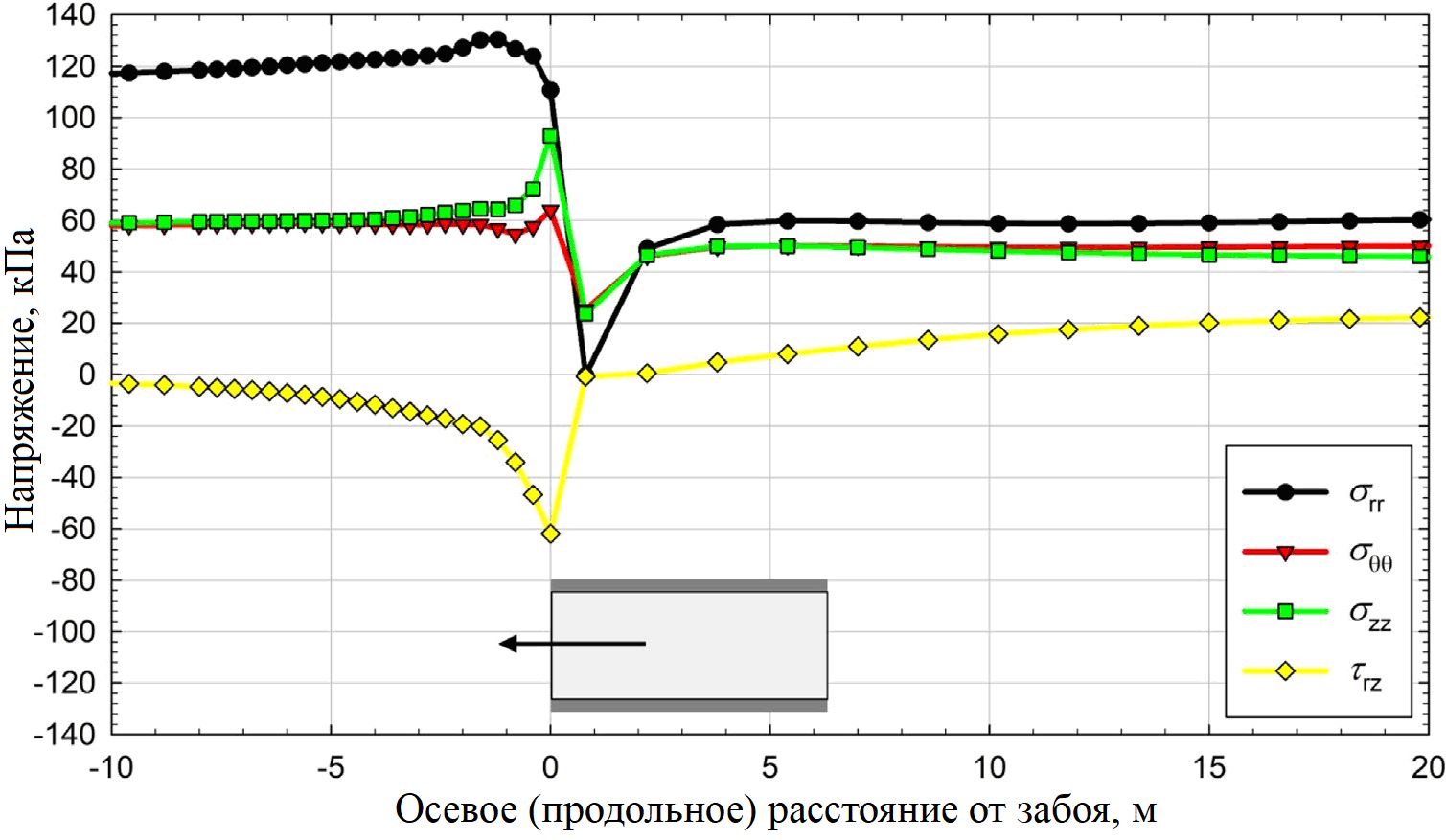
Рис. 12. Напряжения в грунте у свода тоннеля в зависимости от осевого (продольного) расстояния от забоя. Буквенные обозначения: σ_rr – радиальное напряжение; σ_θθ – тангенциальное напряжение; σ_zz – осевое напряжение; τ_rz – осевое напряжение сдвига

(Во второй части статьи, которая будет опубликована в следующем номере журнала «Геоинфо», на примере тоннеля «Параисо» будет рассмотрена оценка воздействия различных стратегий строительства тоннелей новым австрийским методом на деформации грунта и устойчивость забоя. – Ред.).

ИСТОЧНИК ДЛЯ ПЕРЕВОДА

1. Vitali O.P.M., Celestino T.B., Bobet A. Construction strategies for a NATM tunnel in Sao Paulo, Brazil, in residual soil // Underground Space. 2022. Vol. 7. № 1. P. 1–18. doi:10.1016/j.undsp.2021.04.002. URL: doi.org/10.1016/j.undsp.2021.04.002; researchgate.net/publication/351236639_Construction_strategies_for_a_NATM_tunnel_in_Sao_Paulo_Brazil_in_residual_soil.

REFERENCE FOR THE TRANSLATION

1. Vitali O.P.M., Celestino T.B., Bobet A. Construction strategies for a NATM tunnel in Sao Paulo, Brazil, in residual soil. Underground Space. 2022. 7 (1): 1–18. doi:10.1016/j.undsp.2021.04.002. URL: doi.org/10.1016/j.undsp.2021.04.002; researchgate.net/publication/351236639_Construction_strategies_for_a_NATM_tunnel_in_Sao_Paulo_Brazil_in_residual_soil.

СПИСОК ЛИТЕРАТУРЫ, ИСПОЛЬЗОВАННОЙ АВТОРАМИ ПЕРЕВЕДЕННОЙ СТАТЬИ [REFERENCES USED BY THE AUTHORS OF THE TRANSLATED PAPER]

Almeida e Sousa, J., Negro, A., Matos Fernandes, M., & Cardoso, A. S. (2011). Three-Dimensional Nonlinear Analysis of a Metro Tunnel in Sao Paulo Porous Clay, Brazil. Journal of Geotechnical and Geoenvironmental Engineering, 137(4), 376–384.

Azevedo, R. F., Parreira, A., & Zornberg, J. G. (2002). Numerical analysis of a tunnel in residual soils. Journal of Geotechnical and Geoenvironmental Engineering, 128(3), 227–236.

Broere, W. (2016). Urban underground space: Solving the problems of today’s cities. Tunnelling and Underground Space Technology, 55, 245–248.

Cantieni, L., & Anagnostou, G. (2009). The e?ect of the stress path on squeezing behavior in tunneling. Rock Mechanics and Rock Engineering, 42(2), 289–318.

Celestino, T. B., & Ruiz, A. P. T. (1998). Shape of settlement throughs due to tunneling through di?erent types of soft ground. Felsbau, 16, 118–121.

Celestino, T. B., Gomes, R. A. M., & Bortuluci, A. A. (2000). Errors in ground distortions due to settlement through adjustment. Tunnelling and Underground Space Technology, 15(1), 97–100.

Deane, A. P., & Bassett, R.H. (1995). The Heathrow Express trial tunnel. Proceedings of the Institution of Civil Engineers – Geotechnical Engineering, 113(3), 144–156.

Eberhardt, E. (2001). Numerical modelling of three-dimension stress rotation ahead of an advancing tunnel face. International Journal of Rock Mechanics and Mining Sciences, 38(4), 499–518.

Farrell, R., Mair, R., Sciottic, A., & Pigorinic, A. (2014). Building response to tunneling. Soils and Foundation, 54(3), 269–279.

Farias, M. M., Moraes Junior, A. H., & Assis, A. P. (2004). Displacement control in tunnels excavated by the NATM: 3-D numerical simulations. Tunnelling and Underground Space Technology, 19, 283–293.

Golser, J. (2001). Behavior of early-age shotcrete. Proceedings of Shotcrete for Underground Support VIII, 83–93.

HSE (Health and Safety Executive) (1996). Safety of New Austrian Tunneling Method (NATM) Tunnels – A review of sprayed concrete lined tunnels with particular reference to London clay. https://www. hse.gov.uk/pubns/natm.pdf

Lambe, T. W., & Whitman, R. V. (1969). Soil Mechanics. New York, N. Y.: John Wiley and Sons.

Leroueil, S., & Vaughan, P. R. (1990). The general and congruent e?ects of structure in natural soils and weak rocks. Geotechnique, 40(3), 467–488.

Lunardi, P. (2008). Design and Construction of Tunnels – Analysis of Controlled Deformation in Rocks and Soils(ADECO-RS). Berlin Heidelberg: Springer-Verlag.

Mair, R. J., Taylor, R. N., & Bracegirdle, A. (1993). Subsurface settlement pro?les above tunnels in clays. Geotechnique, 43(2), 315–320.

Massad, F., Pinto, C. de S., & Nader, J. J. (1992). Strength and Deformability. Brazilian Society of Soil Mechanics Conference on Soils of Sгo Paulo city, 141–179 (in Portuguese).

MIDAS Information Technology Co. (2019). Midas GTS NX manual.

Marques, F. E. R. (2006). Behavior of Shallow Tunnels in Porous Soils – the Brazilia Metro Case [Doctoral dissertation].University of Coimbra (in Portuguese).

Moller, S. (2006). Tunnel Induced Settlements and Structural Forces in Linings [Doctoral dissertation]. Institute of Geotechnical Engineering, University of Stuttgart.

Nakai, T., Xu, L. M., & Yamazaki, H. (1997). 3D and 2D model tests and numerical analyses of settlements and earth pressures due to tunnel excavation. Soils and Foundations, 37(3), 31–42.

New, B. M., & Bowers, K. H. (1994). Ground movement model validation at the Heathrow Express trial tunnel. Tunneling, 94, 301–329.

Ng, C. W., & Lee, G. T. (2005). Three-dimensional ground settlements and stress-transfer mechanisms due to open-face tunnelling. Canadian Geotechnical Journal, 42(4), 1015–1029.

Ortigao, J. A. R., & Macedo, P. (1993). Large settlements due to tunneling in porous clay. In Proceedings of International Conference on Underground Transportation Infrastructure, AFTES, 119, Sept-Oct 93 (pp. 245–250).

Ortigao, J. A. R., Cunha, R. P., & Alves, L. S. (1995). In-situ tests in Brasilia porous clay. Canadian Geotechnical Journal, 33, 189–198.

Ortigao, J. A. R., Kochen, R., Farias, M. M., & Assis, A. P. (1996). Tunnelling in Brasґэlia porous clay. Canadian Geotechnical Journal, 33 (4), 565–573.

Parreira, A. B. (1991). Analysis of shallow tunnels in soil. The NATM Paraґэso Tunnel at Paulista Avenue in Sгo Paulo City [Doctoral dissertation]. Catholic University of Rio de Janeiro, Rio de Janeiro, Brazil (in Portuguese).

Panet, M., & Guenot, A. (1982). Analysis of convergence behind the face of a tunnel. In Tunnelling 82, Proceedings of the 3rd International Symposium, Brighton (pp. 197–204).

Peck, R. B. (1969). Deep excavation and tunnelling in soft ground. In Proceedings of 7th International Conference on Soil Mechanics and Foundation Engineering, Mexico City, State of the Art Volume (pp. 225–290).

Rabcewicz, L. V. (1964). The new Austrian Tunnelling Method. Water Power, Part 1: November 1964, 571–515.

Rabcewicz, L. V. (1965). The new Austrian Tunnelling Method. Water Power, Part 2: January 1965, 19–24.

Schanz, T., Vermeer, P. A., & Bonnier, P. G. (1999). The hardening soil model: Formulation and veri?cation. In Ronald B. J. Brinkgreve (Eds.), Beyond 2000 in Computational Geotechnics (pp.281–296). Routledge.

Schmidt, B. (1969). Settlements and Ground Movements Associated with Tunneling in Soil [Doctoral dissertation]. University of Illinois.

Vaughan, P. R., & Kwan, C. W. (1984). Weathering, structure and in situ stress in residual soils. Geotechnique, 34(1), 43–59.

Vitali, O. P. M., Celestino, T. B., & Bobet, A. (2019). Buoyancy e?ect on shallow tunnels. International Journal of Rock Mechanics and Mining Sciences, 114(2), 1–6.

Vitali, O. P. M., Celestino, T. B., & Bobet, A. (2018). 3D ?nite element modelling optimization for deep tunnels with material nonlinearity. Underground Space, 3(2), 125–139.

Vitali, O. P. M., Celestino, T. B., & Bobet, A. (2021). New modeling approach for tunnels under complex ground and loading conditions. Soils and Rocks, 44(1) e2021052120.

Volkmann, G. M., & Schubert, W. (2007). Geotechnical Model for Pipe Roof Supports in Tunneling. In Proceedings of the 33rd ITA-AITES World Tunneling Congress (pp. 755–760).