О вкладе веса городов в угрозу затопления прибрежных территорий
Постепенное или периодическое затопление прибрежных регионов становится все более угрожающим во многих местах нашей планеты по ряду причин. Здесь мы предлагаем вниманию читателей краткий обзор материалов статьи сотрудника Геологической службы США Тома Парсонса «Вес городов: воздействие урбанизации на недра Земли» [13], опубликованной в 2021 году в журнале AGU Advances, с использованием информации из некоторых дополнительных источников. Автор указанной статьи вычислил суммарную массу всех зданий высокоурбанизированного региона на побережье залива Сан-Франциско в США и рассмотрел ее распределение по этой территории. Он также создал серию конечноэлементных моделей для изучения воздействий на форму поверхности и подземную среду со стороны распределенного по региону давления от массы зданий. По мнению Парсонса [13], несмотря на то что расчетное снижение абсолютной высоты поверхности прибрежных территорий залива Сан-Франциско под весом городов сравнительно невелико, оно добавляется к оседанию по другим причинам и может усугубить риск затопления, поэтому тоже должно вызывать обеспокоенность ученых и лиц, принимающих решения, особенно учитывая постепенное повышение уровня моря
Введение
Ни для кого не секрет, что на Земле происходит постепенное или периодическое затопление многих прибрежных участков суши, которое становится все более угрожающим не только для отдельных населенных пунктов, но и для целых регионов, а то и стран.
В ряде статей, опубликованных ранее в «Геоинфо» [1–6, 9, 10 и др.], мы обсуждали связь этой опасности с повышением уровня моря теперь уже примерно на 3 мм/год из-за потепления климата, слишком быстрого в последние 100–150 лет по сравнению с предыдущими 0,8–3 млн лет.
Но все же по скоростям развития угрозы затопления на первое место выходит слишком быстрое оседание значительных участков суши по всей планете из-за интенсивной откачки подземных вод для водопотребления, использования в промышленности, орошения сельскохозяйственных земель, полива зеленых насаждений, водопонижения при строительстве котлованов и добыче полезных ископаемых и т. д. По этой причине в XX веке, например, в некоторых районах штата Калифорния США оседание достигло 9 м, в прибрежных японских городах Токио, Осака и Ниигата – 4,7 м, в городе Хьюстон штата Техас США – 4 м, на Тайване – 2,5 м и т. д. Эти процессы также быстро развиваются в Мексике, Венесуэле, Италии, Нидерландах, Иране, Юго-Восточной Азии и во многих других местах по всей планете. Аналогичным образом на понижение уровня суши влияет добыча нефти, газа и других полезных ископаемых. Вопрос слишком быстрого оседания поверхности земли в районах чрезмерной эксплуатации водоносных горизонтов мы рассматривали в обзорах [7, 8], написанных в основном на основе зарубежного опыта [11, 12, 14].
Снижение абсолютных высотных отметок суши может происходить также из-за карстовых и суффозионных процессов, из-за перемещения и естественного уплотнения сжимаемых осадочных отложений, в результате оттаивания многолетней мерзлоты при непродуманном строительстве на ней, под нагрузкой от водохранилищ, отвалов на месторождениях, крупных сооружений и зданий, а также по тектоническим причинам (особенно во время и после землетрясений).
Воздействие на оседание поверхности и на подземную среду именно со стороны нагрузки от веса городов (в результате растущего перераспределения масс на суше) заинтересовало, в частности, Тома Парсонса – сотрудника Геологической службы США (United States Geological Survey – USGS). Результаты своих исследований он изложил в статье «Вес городов: воздействие урбанизации на недра Земли» [13], опубликованной в 2021 году в междисциплинарном журнале AGU Advances («Достижения Американского геофизического союза»). Статьи этого журнала находятся в открытом доступе на бесплатном академическом сайте ResearchGate, но по лицензии Creative Commons Attribution-NonCommercial-NoDerivs License, которая разрешает их некоммерческое использование и распространение на любом носителе при условии, что на оригинальную работу есть правильная ссылка и не производится никаких модификаций или адаптаций. Поэтому мы предлагаем нашим читателям не перевод, а краткий обзор материалов этой статьи (по этой же причине надписи на рисунках со ссылкой на статью [13] не переводились).
Отметим, что исследования Парсонса [13] были профинансированы со стороны Программы Геологической службы США по прибрежным и морским опасностям и ресурсам (USGS Coastal and Marine Hazards and Resources Program).
Сколько весит урбанизированный регион?
Том Парсонс [13] напомнил, что во всем мире продолжается быстрый отток населения из сельской местности в города. В настоящее время в городах проживает около 50% людей на Земле, а к 2050 году, по прогнозам ООН, это число в среднем по планете вырастет до 70%, причем наиболее сильные изменения, вероятно, произойдут в развивающихся странах Африки, Южной и Юго-Восточной Азии.
Поскольку в урбанизированных регионах здания и сооружения бывают сконцентрированы на относительно небольших территориях, а строительные материалы и содержимое возведенных объектов, как правило, бывают ввезены извне, Парсонс [13] задался вопросом о том, каково краткосрочное и долгосрочное воздействие веса городов на земную кору. Для примера он решил исследовать этот вопрос для региона на побережье залива Сан-Франциско в США (рис. 1, 2, а) с населением 7,75 млн человек. Для начала он занялся вычислением общей массы антропогенных объектов и изучением ее распределения на этой территории (рис. 1, 2, а).
![Рис. 1. Расположение региона залива Сан-Франциско на карте США при разном увеличении [15]](/images/dynamic/img44775.jpg)
![Рис. 2. Территория исследуемого региона на карте, обведенная прямоугольником, и застроенные участки, закрашенные черным цветом (а); распределение массы зданий по поверхности данной территории (на цветовой шкале сверху показаны массы зданий в расчете на 1 км<sup>2</sup>, а снизу – изменения нагрузки через эквивалентную толщину слоя воды, м, для сравнения с сезонной нагрузкой) (b); модель исследуемого региона из кубических конечных элементов со стороной 1 км (на цветовой шкале показаны значения модуля Юнга E (кг/(м*с<sup>2</sup>), или Па), которые на изображении модели спроецированы на топографию поверхности, но также меняются и по всему объему модели, что не показано; красными линиями показаны крупные разломы) (c) [13]](/images/dynamic/img44776.jpg)
Но, поскольку учесть все антропогенное, что есть в городах, очень сложно, Парсонс [13] принял, что основная часть массы приходится на здания (всего 964 699 объектов) и на их содержимое. При расчетах Парсонс использовал общедоступную базу данных по контурам и высотам зданий, разработанную корпорацией Microsoft для инвентаризации строений в районе залива Сан-Франциско на основе цифровой модели местности (достоверность данных в этой базе составляла около 93,5%).
Для каждого здания автор работы [13] вычислял площадь пятна застройки, находил координаты центра тяжести и рассчитывал объем, приняв, что все объекты имеют вертикальные стены. Далее он применял минимальные расчетные нагрузки, указанные Американским обществом инженеров-строителей (American Society of Civil Engineers). Для статических (постоянных, от собственного веса) нагрузок он использовал величину 2,0 кН/м2, которая находится в середине диапазона для бетонных полов и стен разных объектов. Для динамических (временных) нагрузок Парсонс [13] применял значение 4,79 кН/м2, что также находится примерно в середине диапазона для разных зданий.
Затем статическая и динамическая нагрузки объединялись, сумма делилась на гравитационную постоянную, а результат умножался на совокупную площадь пятна застройки – и получалась масса объекта с его содержимым в килограммах. Масса самого тяжелого здания на исследуемой территории (международного аэропорта Сан-Франциско) получилась равной 3,35*109 кг (вероятно, этот объект сейчас оседает со скоростью около 4 мм/год). Средняя масса зданий составила 1,64*106 кг. Их приблизительная суммарная масса в исследованном регионе оказалась равной 1,6*1012 кг. Это значение, как подчеркнул Парсонс [13], является ниже реальной массы города, поскольку в расчетах не учитывались дороги, мосты, парки, асфальтированные площадки, инженерные сети и т. д. Поэтому указанный результат автор работы [13] предложил воспринимать как минимальную оценку.
Парсонс [13] также рассчитал распределение городских масс, учитывая массы зданий в проекциях их центров тяжести. Для этого он разбивал карту исследуемой области на квадратные ячейки со стороной 1 км и суммировал массы всех проекций центров тяжести, попавших в каждую ячейку, по всей сетке. Наибольшая концентрация масс, конечно же, пришлась на финансовые центры городов Сан-Франциско, Окленд и Сан-Хосе, где сосредоточено множество высотных зданий на относительно небольших территориях (рис. 2, b).
Автор работы [13] подчеркнул, что население района залива Сан-Франциско выросло примерно со 114 тыс. в 1860 году до более чем 7 млн к настоящему времени. Поэтому и современная «антропогенная масса» также возникла не одномоментно, а росла в процессе урбанизации. То есть воздействие нагрузки от этой массы на земную кору не было мгновенным, а увеличивалось со временем.
Конечноэлементное моделирование. Линейные эффекты от веса зданий
Далее Парсонс [13] выполнил численное моделирование на основе метода конечных элементов для изучения воздействия поверхностной нагрузки в регионе залива Сан-Франциско на упругое поведение самой верхней хрупкой части земной коры, используя в качестве основы подробную геологическую модель.
Рассчитанные массы автор статьи [13] преобразовал в давления, действующие на квадратные участки сетки со стороной 1 км (путем умноженная на гравитационную постоянную и деления на площадь), и приложил эти давления к поверхности конечноэлементной модели земной коры исследуемого региона, построенной с помощью программного комплекса ANSYS©. Модель охватила наиболее густонаселенную часть региона (290 км длиной, 140 км шириной и 10 км толщиной) и совпала с границами подробной трехмерной геологической и сейсмической скоростной модели, созданной Геологической службой США. Она состояла из 406 000 восьмиузловых упругих кубических элементов со стороной 1 км, которые были ограничены снизу и по бокам, а их верх представлял собой свободную поверхность. Парсонс [13] вычислил значения модуля Юнга, используя плотность (ρ), скорости продольных (Vp) и поперечных (Vs) сейсмических волн, представленные в трехмерной геологической модели, в соответствии с зависимостью:

(При этом упругая деформация ε изменяется линейно как функция напряжения σ и модуля Юнга E в соответствии с формулой: ε = σ/E.)
Затем автор работы [13] для каждого отдельного элемента нанес на карту значения E, определяющие его деформационное поведение в ответ на нагрузку (рис. 2, с). (При этом модели было позволено осесть под действием силы тяжести до приложения поверхностного давления.) Таким образом, вариации напряжения и деформации в полученной модели зависели от приложенной нагрузки и свойств материалов земной коры.
В соответствии с расчетным распределением массы (см. рис. 2, b) к верху модели было приложено давление, которое вызвало упругое сжатие, изменения регионального поля напряжений и предполагаемые изменения порового давления воды в подземной среде (рис. 3).
Расчетное упругое сжатие (cм. рис. 3, а) было относительно невелико – с максимальными значениями около 3,2 мм при самых тяжелых нагрузках от наиболее плотно застроенных районов центра Сан-Франциско и долины Санта-Клара (г. Сан-Хосе). Однако, как отметил Парсонс [13], это сжатие может служить лишь минимальной оценкой, поскольку модель была принята как сплошное чисто упругое твердое тело, в то время как реальная земная кора региона пересекается крупными разломами Сан-Андреас и Хейворд (см. рис. 3), множеством более мелких разломов и трещин, а также имеет поры и другие пустоты, которые могут уменьшиться или даже полностью закрыться под нагрузкой, увеличив напряженное состояние
Упругое сжатие, вызванное нагрузками от строительных объектов, приводит к изменениям подповерхностного дифференциального напряжения, которое, в свою очередь, может вызвать горизонтальные деформации и напряжения в дополнение к вертикальному сжатию на поверхности. Максимальные значения приложенных дифференциальных напряжений невелики (0,015 МПа), хотя они сопоставимы со значениями, полученными при нагрузке от водохранилища Андерсон (см. рис. 3, d). При этом, как отметил автор статьи [13], если заполнение водохранилищ или подпитка крупных водоносных горизонтов во время сезонных дождей происходят быстро и могут быть связаны с изменениями частоты и интенсивности землетрясений, то нагрузка от строительных объектов нарастает постепенно по мере роста городов (в регионе залива Сан-Франциско – в основном в течение XX века), что затрудняет определение ее долгосрочного влияния на частоту землетрясений, инструментальное наблюдение за которыми ведется не так долго.
Как уже отмечалось выше, влияние поверхностных нагрузок на подземную среду, вероятно, будет сказываться на состоянии и движении поровой влаги. Под нагрузкой от зданий может уменьшиться и даже полностью закрыться поровое пространство (см. рис. 3, c). Расчетные изменения направлений фильтрационных потоков (см. рис. 3, c) указывают на миграцию поровой воды из областей с наиболее отрицательной дилатансией (с наибольшим уменьшением объема).
Относительные величины и направления радиальных фильтрационных потоков (ur) в замкнутом водоносном горизонте рассчитывались с использованием закона Дарси по формуле:

где k – коэффициент фильтрации пористого грунта; p – поровое давление; r – радиальное расстояние; μ – динамическая вязкость жидкости. (Парсонс [13] здесь вычислял ожидаемые относительные изменения подземных фильтрационных потоков, а не абсолютные и принимал, что величины k и μ остаются постоянными.)
При интегрировании дифференциальное уравнение (2) принимает следующий вид:

где C – принятая константа; r0 – местоположение изменения давления; r – местоположение ожидаемого значения расхода на заданном расстоянии.
Автор работы [13] принял, что изменения отрицательной дилатансии (уменьшение объема) пропорциональны изменениям порового давления, и рассчитывал ожидаемое относительное направление и величину фильтрационного потока от каждой ячейки модели (см. рис. 3, c). Эти расчетные изменения оказались наибольшими под областями самой плотной городской застройки, то есть максимальных приложенных нагрузок (см. рис. 3, c). Предполагаемые фильтрационные потоки на полученной модели находились вдали от зон отрицательной дилатансии, то есть, как правило, вдали от городских районов. Расчетные значения отрицательной дилатансии до минус 0,15 ppm, или минус 1,5*10-5% (ppm – миллионных долей, то есть 1*10-6 от базового показателя), сопоставимы с величинами, вызванными землетрясениями с магнитудой не менее 4 в зоне Паркфилд в Калифорнии, которые также были связаны со значительными изменениями уровня воды в колодцах и скважинах. Это говорит о том, что урбанизация может вызвать серьезные изменения в распределении подземных фильтрационных потоков в рассматриваемом регионе – даже направить их к активным разломам Сан-Андреас и Хейворд (см. рис. 3, с) и повлиять на стабильность этих разломов.
![Рис. 3. Расчетное упругое сжатие, вызванное нагрузкой на поверхность от искусственных сооружений (показано на цветовой шкале в виде оседания поверхности, мм) (а); результирующее изменение дифференциального напряженного состояния, МПа, на глубине 5,5 км (b); отрицательная дилатансия, или уменьшение объема (ppm, то есть миллионные доли) на глубине 5,5 км (ожидаемые изменения в относительных направлениях миграции поровой влаги и в их относительных величинах показаны черными стрелками разного размера) (c); модель изменений высотных отметок, см (слева), и дифференциального напряжения, МПа (справа) при упругом сжатиия под нагрузкой от водохранилища Андерсон (Anderson Reservoir), показывающая, что эти изменения сопоставимы с таковыми от веса сконцентрированных на небольшой площади строительных объектов (0,015 МПа) (d). Черными линиями показаны крупные разломы Сан-Андреас (San Andreas fault) и Хейворд (Hayward fault) [13]](/images/dynamic/img44780.jpg)
Далее Парсонс [13] напомнил, что относительно упругая земная кора «плавает» на более плотном вязкоупругом субстрате, а это означает, что добавление или снятие нагрузки с коры приведет к ее опусканию или подъему соответственно. Это может либо привести к упругому изгибу коры, если она является достаточно целостной (не разбитой разломами), либо может вызвать «погружение» или «всплытие» ограниченного разломами блока.
Чтобы исследовать эти возможности для урбанизированного района залива Сан-Франциско, автор статьи [13] построил простую двухслойную конечноэлементную модель для имитации потенциального прогиба в пределах диска радиусом 1000 км (рис. 4, а). Верхний слой модели соответствовал упругой верхней части земной коры, а нижний слой – вязкоупругой нижней части коры / верхней мантии. Рассчитанная ранее суммарная масса зданий (1,6*1012 кг) была преобразована в давление под действием силы тяжести и распределена как функция Гаусса с центром в круге радиусом 50 км на поверхности модели. Был изучен диапазон упругих мощностей (глубин) от 10 до 100 км в верхнем слое и полный диапазон вязкостей в нижнем слое (от 1018 до 0 Па*с). Прогиб оказался весьма незначительным – максимальное понижение поверхности составило порядка 10-11 мм (см. рис. 4, а).
![Рисунок 4. Смоделированный упругий прогиб, вызванный нагрузкой от искусственных сооружений (а); расчетные изостатические максимальные изменения высоты поверхности блока земной коры между разломами Сан-Андреас и Хейворд в результате нагрузки от городов (вертикальная ось, мм) в зависимости от толщины литосферы (горизонтальная ось, км), если допустить, что этот блок имеет полную свободу подниматься и опускаться, что маловероятно (b); сейсмические исследования методом отраженных волн, показавшие, что эти два разлома проходят через всю толщину земной коры, поэтому промежуточный блок может реагировать на изостатические силы, если он отделен от окружающих частей коры (окружности указывают на гипоцентры землетрясений) (с) [13]](/images/dynamic/img44781.jpg)
Как указал автор работы [13], есть свидетельства того, что крупные разломы Сан-Андреас и Хейворд прорезают земную кору на всю ее толщину и, возможно, затрагивают даже часть верхней мантии, хотя это точно не известно (рис. 4, c). Поэтому возможно, что блок земной коры, который находится между этими двумя разломами, не полностью связан с остальной частью земной коры и может практически независимо от нее опускаться или подниматься под нагрузкой или при ее снятии соответственно. Парсонс [13] исходил из того, что высотная отметка блока земной коры Hc является функцией плотности коры ρc, плотности пластичной астеносферы ρa и толщины этого блока Lc в соответствии с формулой:

Тогда изменение абсолютной высоты поверхности земной коры ΔHc в результате дополнительной нагрузки (которая изменяет плотность столба земной коры до ρc2) будет определяться формулой:
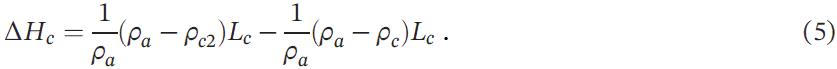
В то время как абсолютная высота поверхности Hc зависит от предполагаемой плотности астеносферы и коры, ее изменение ΔHc зависит только от изменения плотности земной коры из-за добавленного веса городов и от толщины коры.
Напомним, что изостатическое равновесие – это состояние гравитационного равновесия между Земной корой и мантией (или между верхней упругой и нижней упругопластичной частями земной коры). Парсонс [13] указал, что изостатическое изменение абсолютной высоты поверхности зависит от времени, поскольку оно зависит от способности пластичных слоев под упругой верхней частью коры течь (это достаточно долговременный процесс).
Автор статьи [13] принял, что блок земной коры между разломами Сан-Андреас и Хейворд является полностью обособленным и может свободно перемещаться вниз или вверх в течение очень долгого времени. Поэтому он «изолировал» нагрузку от городов на этот блок, вычислил площадь его поверхности, а затем нашел потенциальное изменение изостатической абсолютной высоты его поверхности, которое могло бы произойти для различных величин толщины упругой части коры в результате изменений ее плотности под воздействием нагрузок от зданий (рис. 4, b). Полученные величины снижения высоты поверхности находились в диапазоне от 4 до 25 мм для диапазона «упругой толщины» от 100 до 10 км. Однако в действительности сопротивление трению между сторонами разломов частично или полностью противодействует движению блока. Поэтому указанные числа, как подчеркнул Парсонс [13], представляют собой максимальные изменения изостатической высоты, которые могли бы проявиться в течение многих десятилетий после приложения антропогенной нагрузки или, возможно, во время и после землетрясений, когда разломы «разблокированы».
Таким образом, две изостатические модели, построенные автором работы [13], являются конечными членами ряда – с допущениями либо о полностью целой, либо о полностью разбитой разломами литосфере. Реальный район залива Сан-Франциско находится между этими конечными членами изоморфного ряда. Поэтому также вероятно, что фактическое изостатическое оседание находится между расчетными значениями для конечных членов ряда 0 и 4–25 мм.
Конечноэлементное моделирование. Нелинейные эффекты от веса зданий
Выше моделировалось воздействие нагрузки на верхнюю часть земной коры, поведение которой было принято упругим. Однако, как отметил Парсонс [13], приповерхностные дисперсные грунты и скальные породы редко ведут себя исключительно упруго. Вместо этого они демонстрируют сложный набор нелинейных зависящих от времени механизмов деформации.
Здания обычно строятся на дисперсных грунтах или на трещиноватых скальных породах, которые подвержены сжатию. После первоначального упругого уплотнения грунтов (еще не установившегося) дальнейшее снижение уровня поверхности обычно происходит после строительства. Сложное поведение дисперсных грунтов под нагрузкой обычно зависит от их состава, основных свойств и от времени. В их нелинейном оседании есть по крайней мере две фазы:
- первичное оседание – результат упругого сжатия и вытеснения поровой влаги;
- вторичное оседание – результат долговременной ползучести, которая при постоянно действующей нагрузке может продолжаться практически бесконечно.
Величина и скорость оседания во многом зависят от приложенной нагрузки, локального состава и строения грунтов, порового давления воды и характера фундамента здания. Для крупных зданий обычные расчетные значения осадок составляют около 50–65 мм, хотя в некоторых случаях наблюдаются осадки более 100 мм.
Далее автор работы [13] привел примеры на основе случаев из практики, чтобы проиллюстрировать нелинейное оседание грунтов под нагрузкой от зданий (хотя эти случаи, конечно, не охватывают весь диапазон возможного поведения).
Пример 1. Парсонс [13] выполнил простой конечноэлементный расчет с использованием пакета геомеханических программ COMSOL® для нелинейного первичного оседания глинистого грунта толщиной 10 м, который подвергается равномерно распределенной по площади и линейно возрастающей до 10 кПа нагрузке от высотного дома на площади городского квартала в 100 м2 на основе модифицированной определяющей модели «кэм-клэй» (МКК, modified cam-clay) (рис. 5, а). Первичные осадки получились в диапазоне от 5 до 15 мм в зависимости от количества предполагаемых пустот в смоделированном слое глины.
Вторичная осадка рассчитывалась с использованием уравнения Буйсмана (Buisman, 1936):

где t1 и t2 – время начала и окончания соответственно; Cα' – коэффициент вторичного сжатия, который находится по формуле:

где ep – коэффициент пустотности (пористости) в конце первичного оседания; Cα – коэффициент, который определяется следующим образом:

где Δe – изменение коэффициента пустотности (пористости).
Разумный диапазон значений Cα', как обоснованно подчеркнул Парсонс [13], составляет от 0,0005 до 0,001. На рисунке 5, b показаны примеры сделанных им расчетов вторичного оседания (вертикальная ось, мм) по годам (горизонтальная ось, г.). В результате общее первичное и вторичное оседание получилось в диапазоне 25–55 мм. Соответственно, расчетные скорости оседания поверхности оказались низкими – около 0,07–0,10 мм/год. (Однако на практике наблюдались и более высокие скорости оседания, например 5 мм/год под крупными промышленными объектами в регионе Ломбардия в Италии и 4 мм/год под международным аэропортом Сан-Франциско в США.)
![Рисунок 5. Первичная осадка (вертикальная ось, мм), вызванная начальным уплотнением и обезвоживанием после приложения линейно возрастающей до 10 кПа нагрузки от здания, рассчитанная по дням (горизонтальная ось, сут) для коэффициентов пустотности 1,0; 0,5 и 0,1 (а); расчетная долговременная вторичная осадка (в результате ползучести), вызванная перегруппировкой частиц грунта и другими нелинейными эффектами для коэффициентов вторичного сжатия 0,0005; 0,00075 и 0,001 (b); конечноэлементная модель площадью 100 м * 100 м и толщиной 10 м под равномерно распределенной нагрузкой в 10 кПа (цветовая шкала отражает величину оседания поверхности, мм) (с) [13]](/images/dynamic/img44787.jpg)
Пример 2. Продолжительность вторичного оседания можно проиллюстрировать на примере острова Трежер (Treasure Island – остров Сокровищ). Это искусственный остров в центральной части залива Сан-Франциско в основном из гидронамывного песка и грязи, созданный в 1936 году к Международной выставке «Голден гейт» и расположенный в центральной части залива Сан-Франциско. Искусственно намытые песчано-глинистые отложения мощностью 10,7–15,2 м заняли площадь около 5 500 м * 1 600 м, то есть их объем составил 2,08*107 м3. Умножение на характерную для таких отложений плотность 2 007 кг/м3 дало общую массу 4,16*1010 кг, или 4,73*109 кг/км2, что сопоставимо с максимальной массой от зданий в рассматриваемом исследовании [13], равной 3,5*109 кг/км2. Остров Трежер в настоящее время оседает со скоростью не менее 4 мм/год (как и другие участки прибрежной зоны залива, подвергшиеся мелиорации). Если это началось после строительства острова в 1936 году, то, как отметил автор работы [13], это согласуется с предположением о том, что вторичная ползучесть может быть неопределенной.
Парсонс [13] отметил, что твердая скальная порода также подвержена зависящей от времени нелинейной деформации, известной как «хрупкая ползучесть», или «ползучесть с хрупким разрушением» (brittle creep). Такая ползучесть происходит с химически активированным субкритическим растрескиванием (subcritical cracking). Однако лабораторные эксперименты показали, что начало «хрупкой ползучести» для большинства горных пород требует значений дифференциального напряжения порядка сотен мегапаскалей (МПа), тогда как расчетное дифференциальное напряжение от строительных нагрузок оказалось на порядки меньше, составив около 0,01 МПа (см. рис. 3, b). Таким образом, маловероятно, что строительные нагрузки инициируют «хрупкую ползучесть» в неповрежденной скальной породе. Автор статьи [13] проверил это, заменив упругие элементы в региональной конечноэлементной модели упругими/пластическими элементами в программной системе ANSYS© для моделирования нелинейного поведения скальных пород, которые могут демонстрировать остаточную деформацию из-за растрескивания. Результаты применения линейно изменяющейся во времени нагрузки (см. рис. 2, b) не показали значительной ползучести от растрескивания. Значения осадки в этом случае получились такими же, как и в случае чисто упругой модели (см. рис. 3).
Заключение
Итак, оцененная автором статьи [13] минимальная суммарная масса зданий в районе залива Сан-Франциско составила 1,6*1012 кг. Упругая конечноэлементная модель изучаемого региона показала осадки от 0,2 до 3,2 мм. В случае «плавающего» на мантии изолированного разломами блока земной коры в центре зоны залива Сан-Франциско оседание составило от 0 до 20 мм в зависимости от трения по стенкам разломов. В случае моделирования нелинейно развивающегося первичного и вторичного оседания глинистых грунтов совокупное понижение уровня поверхности попало в диапазон 20–55 мм за 100 лет.
В целом расчеты Парсонса [13] показали, что в результате урбанизации в районе залива Сан-Франциско можно ожидать совокупного оседания не менее 5–80 мм в любой заданной точке. Хотя в исследуемом регионе есть и более экстремальные примеры. Пятидесятивосьмиэтажный небоскреб Миллениум-Тауэр (Millennium Tower) в Сан-Франциско, построенный в 2009 году, за 10 лет осел более чем на 40 см (точнее, осел на 43 см и наклонился на 36 см к северо-западу. – Ред.). Скорость оседания территории международного аэропорта Сан-Франциско, находящегося на побережье залива, составляет 4 мм/год. С помощью спутникового интерферометрического радара с синтезированной апертурой (InSAR) Европейского космического агентства можно наблюдать оседание некоторых высотных зданий в Сан-Франциско со скоростью до 20 мм/год.
Основные результаты воздействия давления от строительных объектов – закрытие порового пространства, перенаправление фильтрационных потоков в подземной среде и (особенно) нелинейное оседание и ползучесть грунтов, вызывающие понижение уровня поверхности земли.
Как подчеркнул автор работы [13], указанный диапазон оседания 5–80 мм не основан на учитывающем все факторы моделировании в каждом конкретном месте, а предназначен для иллюстрации относительного воздействия городов на земную кору. Полученные результаты расчетов следует рассматривать как минимальные, потому что были учтены не все источники антропогенной массы.
Средние наблюдаемые скорости оседания в районе залива Сан-Франциско составляют 1–2 мм/год. Воздействие на понижение уровня поверхности со стороны всех факторов (веса городов, чрезмерной откачки подземных вод, тектонических движений, эрозии, перераспределения городских отложений и пр.) усугубляется изменением уровня моря, который в районе залива Сан-Франциско к 2050 году, вероятно, повысится на 200–300 мм, что значительно увеличит вероятность регионального затопления.
То же происходит и во многих других частях мира. Ускорение миграции людей в прибрежные урбанизированные регионы подвергает риску эти группы населения, и этот риск с течением времени увеличивается из-за дальнейшего роста городов и увеличения грандиозности возводящихся в них зданий и сооружений. Тем более что, как отметил Парсонс [13], городские дренажные сети и мощеные улицы способствуют транспортировке наносов вместе с поверхностным стоком из городов в незастроенные районы, что уменьшает нормальное накопление осадочных отложений, которые могли бы позволить урбанизированной территории хотя бы частично восстановить уровень поверхности. Конечно, производится рекультивация прибрежных земель с помощью насыпных грунтов, которая локально повышает уровень поверхности, но вскоре в результате уплотнения и/или эрозии он снова может упасть.
Автор статьи [13] выразил надежду, что результаты, полученные для района залива Сан-Франциско по воздействию антропогенной нагрузки на уровень поверхности, могут быть применимы к любому крупному городу, что особенно важно для тектонически активных окраин континентов. Он отметил, что представленные в его работе [13] методы можно будет улучшить, используя спутниковые или аэрофотоснимки для более детального анализа зон вероятных наводнений или затопления.
Источники
- Глобальные изменения климата. Часть 1. Происходит ли потепление и почему? // Геоинфо. 23.04.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/globalnye-izmeneniya-klimata-chast-1-proiskhodit-li-poteplenie-i-pochemu-40679.shtml.
- Глобальные изменения климата. Часть 2. Насколько человечество виновно в потеплении? // Геоинфо. 20.05.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/globalnye-izmeneniya-klimata-chast-2-naskolko-chelovechestvo-vinovno-v-poteplenii-40768.shtml.
- Глобальные изменения климата. Часть 3. Последствия потепления // Геоинфо. 03.06.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/globalnye-izmeneniya-klimata-chast-3-posledstviya-potepleniya-40857.shtml.
- Глобальные изменения климата. Часть 4. Что делать? // Геоинфо. 10.06.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/globalnye-izmeneniya-klimata-chast-4-chto-delat-40875.shtml.
- Исчезнет ли Венеция? Часть 1. Город и вода // ГеоИнфо. 12.02.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/ischeznet-li-veneciya-chast-1-gorod-i-voda-39926.shtml.
- Исчезнет ли Венеция? Часть 2. Проекты по спасению города // ГеоИнфо. 18.02.2019. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/ischeznet-li-veneciya-chast-2-proekty-po-spaseniyu-goroda-40028.shtml.
- Моделирование в PLAXIS. Причины оседания поверхности земли на орошаемых территориях вблизи угольного карьера // ГеоИнфо. 28.01.2021. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/modelirovanie-v-plaxis-prichiny-osedaniya-poverhnosti-zemli-na-oroshaemyh-territoriyah-vblizi-ugolnogo-karera-43965.shtml.
- Чем грозит чрезмерная эксплуатация водоносных горизонтов в глобальном масштабе // Геоинфо. 29.03.2021. URL: geoinfo.ru/product/analiticheskaya-sluzhba-geoinfo/chem-grozit-chrezmernaya-ehkspluataciya-vodonosnyh-gorizontov-v-globalnom-masshtabe-44369.shtml.
- Шац М.М. Последствия изменения климата. Часть 1. Основные подходы к стратегии развития цивилизации. Управление климатом // Геоинфо. 08.04.2021. URL: geoinfo.ru/product/shac-mark-mihajlovich/posledstviya-izmeneniya-klimata-chast-1-osnovnye-podhody-k-strategii-razvitiya-civilizacii-upravlenie-klimatom-44435.shtml.
- Шац М.М. Последствия изменения климата. Часть 2. Адаптация к глобальным изменениям климата // Геоинфо. 15.04.2021. URL: geoinfo.ru/product/shac-mark-mihajlovich/posledstviya-izmeneniya-klimata-chast-2-adaptaciya-k-globalnym-izmeneniyam-klimata-44465.shtml.
- Herrera-Garcнa G., Ezquerro P., Tomas R., Bejar-Pizarro M., Lopez-Vinielles J., Rossi M., Mateos R. M., Carreon-Freyre D., Lambert J., Teatini P., Cabral-Cano E., Erkens G., Galloway D., Hung W.-Ch., Kakar N., Sneed M., Tosi L., Wang H., Ye Sh. Mapping the global threat of land subsidence // Science. AAAS, 2021. Vol. 371. Issue 6524. P. 34–36. URL: science.sciencemag.org/content/371/6524/34.full?ijkey=7QWDaczKcM3h2&keytype=ref&siteid=sci.
- Herrera-Garcнa G., Ezquerro P., Tomas R., Bejar-Pizarro M., Lopez-Vinielles J., Rossi M., Mateos R. M., Carreon-Freyre D., Lambert J., Teatini P., Cabral-Cano E., Erkens G., Galloway D., Hung W.-Ch., Kakar N., Sneed M., Tosi L., Wang H., Ye Sh. Supplementary materials // Science. AAAS, 2021. Vol. 371. Issue 6524. URL: science.sciencemag.org/content/suppl/2020/12/29/371.6524.34.DC1.
- Parsons T. The weight of cities: urbanization effects on Earth's subsurface // AGU Advances. 2021. Vol. 2. Research article e2020AV000277. DOI: https://doi.org/ 10.1029/2020AV000277.
- Tzampoglou P., Loupasakis C. Numerical simulation of the factors causing land subsidence due to overexploitation of the aquifer in the Amyntaio open coal mine, Greece // HydroResearch. Vol. 1. Elsevier B.V.: June 2019. P. 8–24. URL: sciencedirect.com/science/article/pii/S2589757819300034.
- yandex.ru/maps.
Журнал остается бесплатным и продолжает развиваться.
Нам очень нужна поддержка читателей.
Поддержите нас один раз за год
Поддерживайте нас каждый месяц
















