Схематизация свойств грунтов при математическом моделировании в инженерной геологии и геотехнике

Кургузов Константин Владимирович

Преподаватель кафедры инженерной геологии Гидрогеологического факультета МГРИ, к.г-м.н.

Новгородова Маргарита Алексеевна

Ассистент кафедры инженерной геологии Гидрогеологического факультета МГРИ

Сироткина Ольга Николаевна

Старший научный сотрудник Геологического факультета МГУ им. М.В. Ломоносова, к.г-м.н.

Введение

Одним из главных этапов построения инженерно-геологической модели является схематизация. Схематизация может быть обобщенной и специальной.

Под обобщенной схематизацией, в данном контексте, можно понимать процесс упрощения реального природного объекта, обладающего бесконечной степенью сложности, до концептуальной модели, ограниченной рамками научного познания.

Специальная схематизация предполагает упрощение концептуальной модели до специализированной схемы, способной в рамках поставленной задачи в определенной мере сохранить адекватность с исходной концептуальной моделью. Цель специальной схематизации может быть выражена в виде следующего тезиса: максимальное упрощение при минимальной потере адекватности. Этот тезис может служить также основой для математической постановки задачи.

Специальную схематизацию можно разделить на несколько взаимосвязанных этапов: схематизацию поведения, схематизацию структуры, схематизацию свойств и схематизацию состояния объекта моделирования [1].

В основе специальной инженерно-геологической схематизации лежит понятие инженерно-геологического элемента (ИГЭ). Согласно российским нормам (СП 446.1325800.2019) [2] «ИГЭ – основная грунтовая единица, используемая при создании инженерно-геологической модели грунтового массива, включающая некоторый объем грунта одного и того же типа (подтипа), вида (подвида) и разновидности при изменении значений характеристик грунта в пределах элемента случайно (незакономерно) или при наблюдающейся закономерности изменения характеристик грунтов с коэффициентом вариации для физических характеристик грунта ≤ 0,15, для механических ≤ 0,30».

Несмотря на тот факт, что случайная природа распределения свойств в ИГЭ присутствует в определении, до недавнего времени этому факту при построении инженерно-геологических моделей уделялось недостаточно внимания, статистическая обработка свойств грунтов выполнялась до создания модели, а сама модель носила, как правило, детерминированный характер.

Однако в последние годы ситуация изменилась. В первую очередь это связано с развитием, преимущественно за рубежом, нового научного направления – стохастической геотехники [3], одной из главных задач которой является учет неопределенности при математическом моделировании литотехнических систем. Второй важной задачей стохастической геотехники является анализ рисков при создании и эксплуатации ЛТС [4].

В настоящее время можно выделить четыре основных модели, описывающих распределение свойств грунтов при математическом моделировании в инженерной геологии и геотехнике.

Рассмотрим их на примере решения задачи по оценке устойчивости склонов методами предельного равновесия на основе критерия прочности Кулона-Мора.

Рис. 1. Расположение исследуемого участка (красный прямоугольник)

В административном отношении участок работ расположен в г. Москва, пос. Лапшинка (рис. 1).

В геоморфологическом отношении исследуемая территория расположена в пределах пологоволнистой моренной равнины, слабо расчлененной, с хорошо разработанными речными долинами. Рельеф характеризуется абсолютными высотными отметками поверхности порядка 180,35 – 182,05 м.

В геологическом строении до разведанной глубины 20,0 м принимают участие четвертичные отложения, представленные техногенными перемещенными грунтами, аллювиальными, покровными, ледниковыми и меловыми отложениями. Гидрогеологические условия характеризуются близким залеганием грунтовых вод, а также наличием большого количества водоносных горизонтов, гидравлически связанных друг с другом.

В пределах исследуемого участка техногенные перемещенные грунты, слагающие тело отвала, представлены суглинком коричневым, слабоуплотненным, тугопластичным. Они были вскрыты при проведении буровых работ во всех скважинах. Мощность техногенных грунтов изменяется от 2,7 м до 12,0 м.

При проведении инженерно-геологических работ на исследуемой территории была отмечена активизация склоновых процессов (рис. 2).

Рис. 2. Трещины закола на бровке насыпи

Расчетные схемы и исходные данные

Как уже отмечалось выше, отвал сложен техногенными грунтами. Значения показателей физических и механических свойств техногенных грунтов, залегающих в пределах исследуемого участка, сильно отличаются от прочих, образованных в природе, грунтов. Распределение свойств в техногенных грунтах характеризуется большой неоднородностью. По этой причине выделение различных по физико-механическим свойствам слоёв и задание в их пределах расчетных значений характеристик представляет определённую сложность.

Учитывая вышесказанное, с целью оценки корректности закладываемых в расчет устойчивости склона свойств грунтов, моделирование было выполнено по следующим схемам:

1. Детерминированная модель

При решении поставленной задачи исходными параметрами являются определенные для каждого ИГЭ скалярные величины свойств грунтов: плотности, удельного сцепления, угла внутреннего трения (рис. 3).

Рис. 3. Модель распределения удельного сцепления при детерминированной модели задания свойств и результаты расчета устойчивости склона

Результатом решения является определение минимального значения коэффициента устойчивости (также скалярной величины) и нахождение положения соответствующей ему поверхности скольжения (рис. 3).

2. Интерполяционная модель

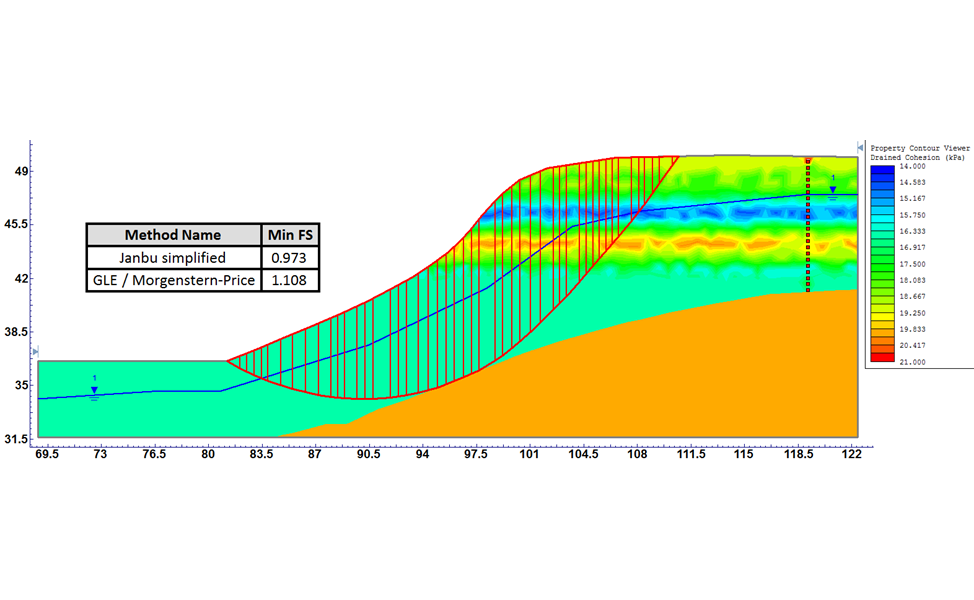
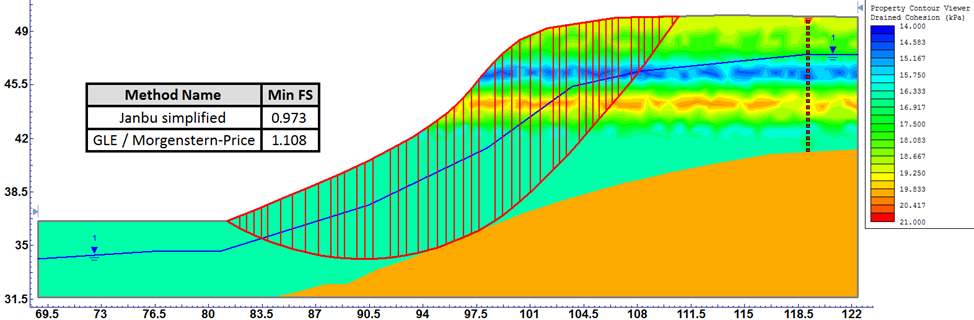
В данном случае исходными параметрами являются определенные для каждого ИГЭ числовые массивы, включающие свойства грунтов (плотность, удельное сцепление, угол внутреннего трения) и координаты места отбора пробы для определения свойств. На основе этой информации с использованием интерполяционных методов для каждого ИГЭ строится поле распределения свойств (рис. 4).

Результатом решения, как и в случае детерминированной модели, является определение минимального значения коэффициента устойчивости и нахождение положения соответствующей ему поверхности скольжения (рис. 4). Однако следует заметить, что результат зависит от выбора метода интерполяции свойств грунтов [5].

Рис. 4. Модель распределения удельного сцепления при интерполяционной модели задания свойств и результаты расчета устойчивости склона

3. Вероятностная модель

В отличие от описанных выше моделей, исходными параметрами в данном случае являются не скалярные величины, а функции вероятностного распределения свойств грунтов [11].

Главной проблемой при построении вероятностной модели является определение закона распределения случайных величин. В случае нормального распределения для построения вероятностной функции необходимы два параметра – математическое ожидание и дисперсия.

Результатом решения, в этом случае является вероятностная функция распределения К_у, на основе которой можно определить вероятность развития оползневого процесса (рис. 5).

Рис. 5. Интегральная функция распределения Ку (вероятность развития оползневого процесса 42%)

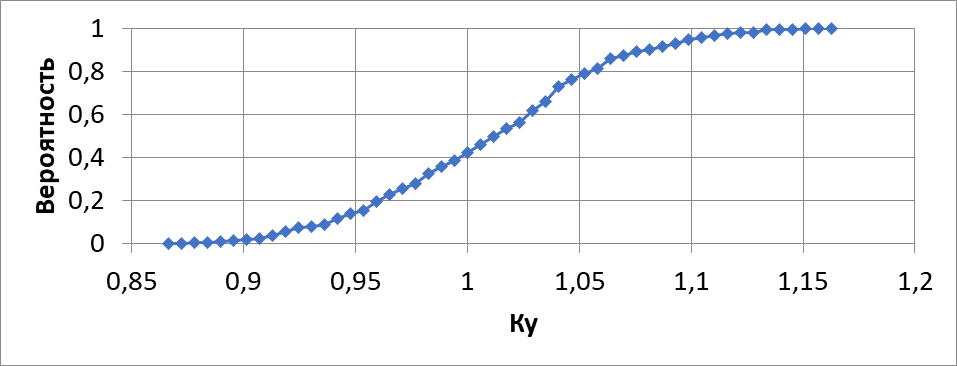
Изменчивость свойств грунтов по-разному влияет на величину К_у. Анализ чувствительности близок по сути к вероятностному анализу, однако вместо задачи о вероятности развития оползневого процесса в зависимости от изменчивости свойств грунтов, в этом случае решается задача зависимости коэффициента устойчивости от закономерного изменения тех или иных параметров. Следует заметить, что критическими параметрами прочности является не пара значений (угол внутреннего трения - сцепление), а функция, определяемая данными параметрами, которая может служить критерием прочности склона (по аналогии с критерием прочности пород, слагающих склон). Определить эту зависимость позволяет двухфакторный анализ чувствительности (рис. 6)

Рис. 6. Двухфакторный анализ чувствительности для моделируемого склона. Красная линия – зависимость угла внутреннего трения от сцепления при которой Ку склона равен 1

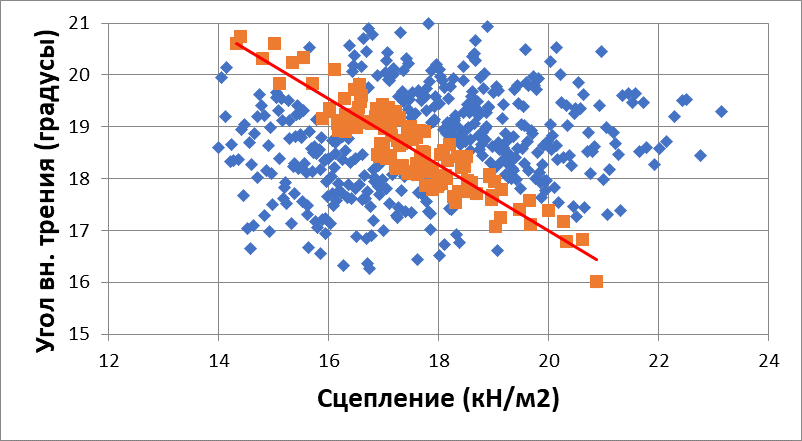
4 .Модель изменчивости

Не учет случайной компоненты в структуре численных оценок геологического параметра (использование чисто детерминированных моделей) достаточно часто приводит к ошибочным результатам [10].

Пространственная изменчивость свойств грунта может быть смоделирована с помощью теории случайных полей [6], согласно которой в любой области ИГЭ свойства грунта являются случайной переменной, характеризующейся вероятностной функцией распределения и коррелирующей со значениями свойств грунта в смежных областях [7]. Пространственная корреляция свойств грунта определяется на основе функции автокорреляции, которая может быть оценена по результатам измерений параметра в различных точках по результатам полевых или лабораторных испытаний [8].

Корреляционная структура случайной Гауссовой области может быть определена с помощью функции коэффициента корреляции Маркова:

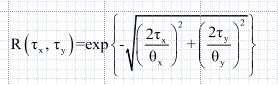
где R(τ_x , τ_y) – коэффициент автокорреляции, τ_x and τ_y - абсолютные расстояния между двумя точками в горизонтальном и вертикальном направлениях соответственно, θx and θ_y – корреляционные расстояния в горизонтальном и вертикальном направлениях соответственно [9] .

Таким образом, необходимыми исходными параметрами для модели изменчивости дополнительно к функции вероятностного распределения свойств грунтов являются величины корреляционного расстояния.

Для исследования влияния пространственной изменчивости прочностных параметров грунта на вероятность разрушения откосов дамбы был использован случайный метод предельных равновесий (RLEM) [12, 13].

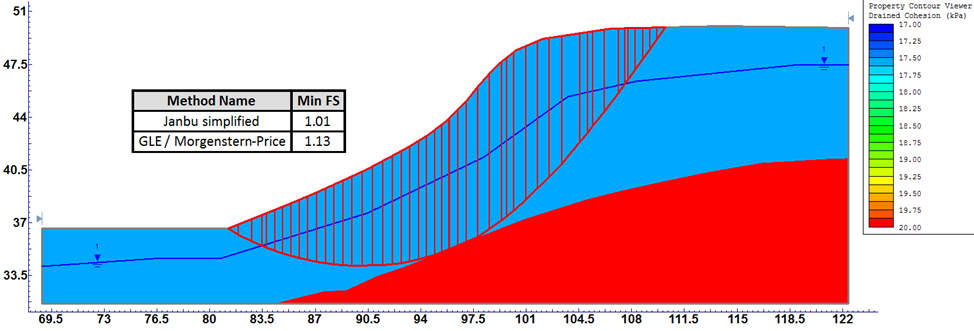
Результатом решения в этом случае являются вероятные модели распределения свойств грунтов для заданного корреляционного расстояния и функция распределения К_у (рис. 7).

Рис. 7. Модель распределения удельного сцепления для: а) среднего значения Ку -1,01; б) минимального значения Ку=0,97. Горизонтальное корреляционное расстояние 1м, вероятность развития оползневого процесса 53,6%

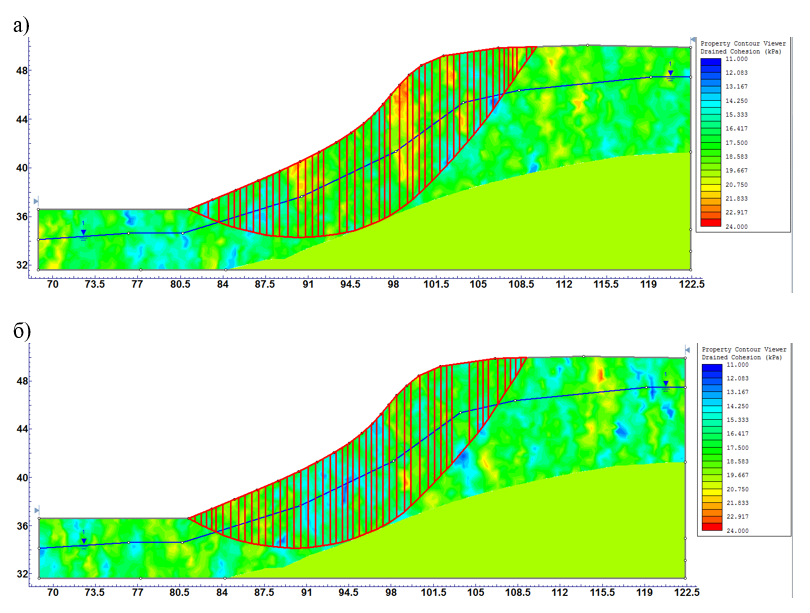
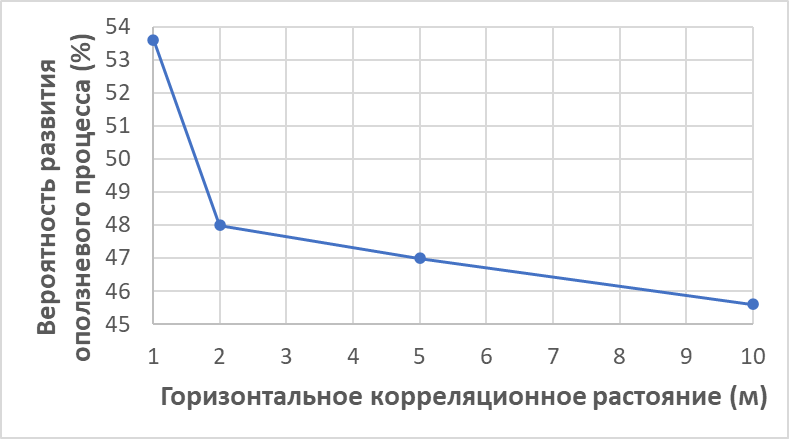
Анализ результатов расчета показал, что величина корреляционного расстояния не влияет на К_у склона (для всех случаев средний Fs=1.01). Однако, вероятность развития оползневого процесса при изменении величины корреляционного расстояния меняется. При этом с уменьшением корреляционного расстояния и, как следствие, с возрастанием неоднородности в грунтах, вероятность развития оползневого процесса возрастает (рис. 8).

Рис. 8. Зависимость вероятности развития оползневого процесса от горизонтального корреляционного расстояния

Заключение

Отсутствие полноты информации о составе, строении и свойствах литотехнических систем, о законах проходящих процессов, зачастую вызывает вопросы при проектировании и строительстве объектов. Сбор, накопление и анализ данных, как правило, сопровождаются ошибками измерений, искажающими и без того ограниченную информацию об инженерно-геологических условиях. Эти и многие другие факторы являются следствием неопределенности при изучении состояния и прогнозе поведения ЛТС [10].

Понятие неопределенности тесно связано с понятиями неоднородности и изменчивости. В настоящее время можно выделить четыре основных модели, описывающих распределение свойств грунтов при математическом моделировании в инженерной геологии и геотехнике – детерминированную модель; интерполяционную модель; вероятностную модель; модель изменчивости. Выбор той или иной модели определяет результат моделирования.

В данном исследовании мерой неопределенности являются вероятностная природа свойств грунтов и величина корреляционного расстояния. Изучение и анализ неопределенности сводится к двум задачам: к построению расчетной модели неопределенности с количественным описанием различных аспектов и к последующему учету данной модели в стохастических расчетах.

Для решения данной задачи на примере оценки устойчивости склона был использован случайный метод предельных равновесий (RLEM). Анализ результатов исследования показал, что в условиях неопределенности К_у склона не является надежным параметром, характеризующим устойчивость. С увеличением неоднородности грунтов, слагающих склоновый массив, средний К_у не меняется, однако вероятность развития оползневого процесса возрастает.

Список литературы

1. Фоменко И.К. Математическое моделирование напряженного состояния инженерно - геологического массива, сложенного анизотропными горными породами // автореферат дис... канд.геол.минер. наук: 04.00.07. Москва. 2001. С. 24.

2. СП 446.1325800.2019 (Инженерно-геологические изыскания для строительства. Общие правила производства работ)

3. Griffiths, D. & Fenton, Gordon. (2007). Probabilistic Methods in Geotechnical Engineering. 10.1007/978-3-211-73366-0

4. Fenton G.A., Griffith D.V. Risk assessment in geotechnical egnineering — NewJersey: WILEY, 2008

5. Буфеев Ф. К., Фоменко И. К., Сироткина О. Н. Влияние методов интерполяции прочностных свойств грунтов на результаты расчета устойчивости склонов // Международный научно-исследовательский журнал. — 2016. — С. 127–133. DOI: 10.18454/IRJ.2227-6017

6. Vanmarcke, E., (1983), “Random Fields: Analysis and Synthesis,” MIT Press, Cambridge, MA

7. El-Ramly, H. and Morgenstern, N. and Cruden, D., (2002), “Probabilistic slope stability analysis for practice,” Can. Geot. J., 39(3), pp. 665-683

8. Baecher, G.B. and Christian, J.T., (2005), “Reliability and Statistics in Geotechnical Engineering,” John Wiley & Sons

9. Javankhoshdel, Sina & Cami, Brigid & Bathurst, Richard & Corkum, Brent. (2018). Probabilistic Analysis of Layered Slopes with Linearly Increasing Cohesive Strength and 2D Spatial Variability of Soil Strength Parameters Using Non-Circular RLEM Approach. 10.1061/9780784481585.014

10. Кургузов К. В., Фоменко И. К., Сироткина О. Н. Вероятностно-статистические подходы при оценке неопределенности литотехнических систем // Геоэкология. Инженерная геология. Гидрогеология. Геокриология. — 2020. — № 2. — С. 80–89. 

11. Зеркаль О. В., Фоменко И. К. Влияние различных факторов на результаты вероятностного анализа активизации оползневых процессов // Инженерная геология. — 2016. — № 1. — С. 16–21.

12. Javankhoshdel, Sina & Luo, Ning & Bathurst, Richard. (2016). Probabilistic analysis of simple slopes with cohesive soil strength using RLEM and RFEM. Georisk: Assessment and Management of Risk for Engineered Systems and Geohazards. 1-16. 10.1080/17499518.2016.1235712.

13. Izadi, Ardavan & Chenari, Reza & Cami, Brigid & Javankhoshdel, Sina. (2020). Full and Quasi-Stochastic Slope Stability Analyses using Random Limit Equilibrium Method (RLEM).